What's 17 Out Of 20
scising
Sep 22, 2025 · 6 min read
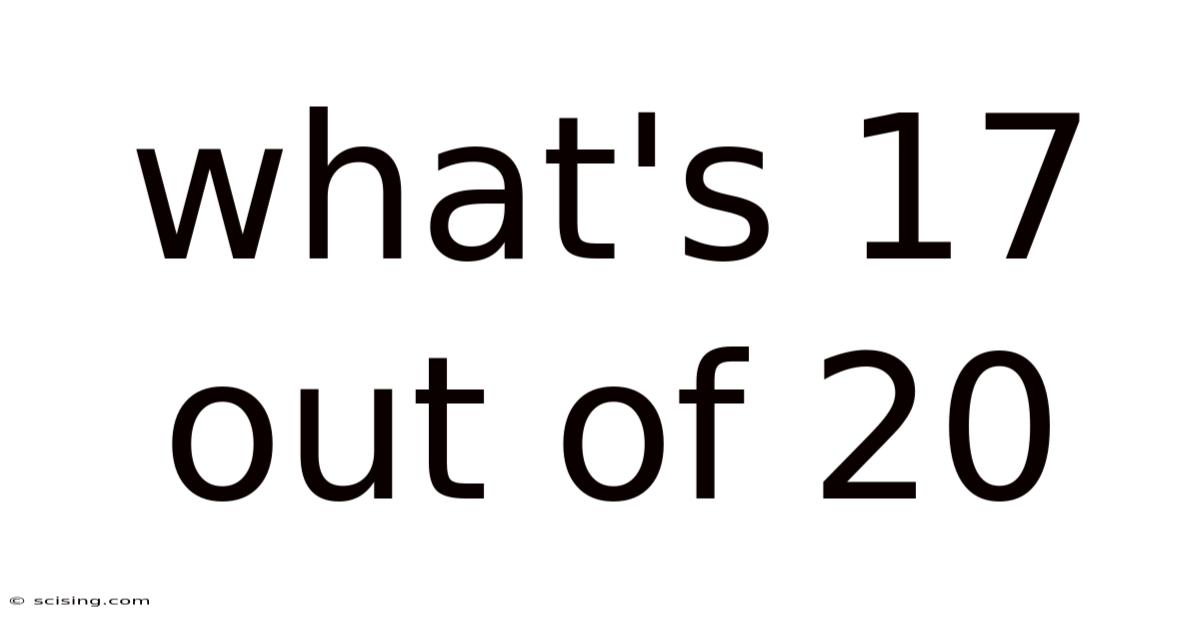
Table of Contents
What's 17 out of 20? Understanding Fractions, Percentages, and Decimals
"What's 17 out of 20?" This seemingly simple question opens the door to a world of mathematical concepts, from basic fractions to percentages and decimals, all crucial for everyday life and advanced studies. This article will not only answer the question directly but also delve into the underlying principles, showing you how to calculate similar problems and apply these skills in various contexts. We'll explore different ways to represent this fraction, highlighting their practical applications and building a strong foundation in numerical understanding.
Understanding Fractions: The Foundation
The phrase "17 out of 20" is inherently a fraction. A fraction represents a part of a whole. In this case, the whole is 20, and the part we're interested in is 17. We write this fraction as 17/20. The number on top (17) is called the numerator, representing the part, and the number on the bottom (20) is the denominator, representing the whole.
This fraction, 17/20, is already in its simplest form. We can't simplify it further because 17 is a prime number (only divisible by 1 and itself), and it doesn't share any common factors with 20 other than 1. If we had a fraction like 10/20, we could simplify it by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 10, resulting in 1/2.
Understanding the concept of fractions is paramount. Whether you're dividing a pizza, calculating a discount, or understanding statistical data, fractions are fundamental to many everyday calculations.
Converting Fractions to Decimals: A Step-by-Step Guide
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
17 ÷ 20 = 0.85
Therefore, 17 out of 20 is equal to 0.85 as a decimal. This decimal representation is particularly useful when dealing with monetary values, measurements, or data in spreadsheets and other digital applications. The decimal form makes comparisons and calculations easier in certain contexts.
Converting Fractions to Percentages: Expressing Parts as Wholes
Percentages express a fraction as a portion of 100. To convert a fraction to a percentage, we first convert it to a decimal (as we did above) and then multiply by 100%.
0.85 x 100% = 85%
So, 17 out of 20 is equal to 85%. Percentages are frequently used to represent proportions, progress, changes, and rates in a way that is easily understood across various disciplines. For example, a student scoring 17 out of 20 on a test achieved an 85% score.
Visualizing 17 out of 20: A Pictorial Representation
Imagine a pizza cut into 20 equal slices. If you eat 17 of those slices, you've eaten 17/20 or 85% of the pizza. This visual representation helps solidify the understanding of the fraction, decimal, and percentage equivalencies. Similarly, you could imagine a bar graph with 20 segments; shading 17 of them illustrates the same concept.
Real-World Applications of 17 out of 20
The ability to understand and work with fractions, decimals, and percentages is essential across various aspects of life:
-
Academic Performance: As mentioned earlier, a test score of 17 out of 20 translates to a strong 85% grade. Understanding these conversions is vital for evaluating academic progress.
-
Financial Literacy: Calculating discounts, interest rates, and tax percentages all rely on the ability to work with fractions and percentages. For example, an 85% discount on a $100 item would result in a saving of $85.
-
Data Analysis: Many professions rely on analyzing data expressed as percentages or fractions. Understanding these representations is crucial for interpreting findings and making informed decisions. For example, 85% market share indicates significant dominance in a given industry.
-
Everyday Calculations: Dividing resources, sharing costs, or calculating proportions in recipes often involves working with fractions.
-
Science and Engineering: In scientific fields and engineering, working with proportions, ratios, and percentages is crucial for accurate measurements, calculations, and analysis.
Expanding the Concept: Working with Different Fractions
Let's look at how to apply the same principles to other fractions:
Example 1: What's 12 out of 15?
- Fraction: 12/15
- Simplification: Both 12 and 15 are divisible by 3, so we simplify to 4/5.
- Decimal: 4 ÷ 5 = 0.8
- Percentage: 0.8 x 100% = 80%
Example 2: What's 7 out of 25?
- Fraction: 7/25
- Decimal: 7 ÷ 25 = 0.28
- Percentage: 0.28 x 100% = 28%
These examples illustrate the consistent application of the principles discussed earlier. The ability to convert between fractions, decimals, and percentages provides flexibility and allows for choosing the most appropriate representation depending on the context.
Frequently Asked Questions (FAQ)
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Q: How do I convert a decimal to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). Then, simplify the fraction. For example, 0.75 becomes 75/100, which simplifies to 3/4. 0.8 becomes 8/10, which simplifies to 4/5.
Q: What if the fraction cannot be simplified?
A: Some fractions, like 17/20, cannot be simplified because the numerator and denominator share no common factors other than 1. This doesn't affect the ability to convert it to a decimal or percentage.
Q: Are there any online tools or calculators for fraction, decimal, and percentage conversions?
A: Yes, many online tools and calculators are readily available to assist with these conversions. These tools can be helpful for checking your work or for quickly converting large numbers of values.
Conclusion: Mastering the Fundamentals
Understanding "what's 17 out of 20" extends far beyond a simple numerical answer. It's about grasping the fundamental concepts of fractions, decimals, and percentages, their interrelationships, and their applications in various aspects of life. By mastering these fundamental concepts, you equip yourself with essential tools for tackling a wide range of mathematical problems and confidently navigating numerical challenges in academic, professional, and personal contexts. The ability to seamlessly convert between these representations is a cornerstone of mathematical literacy and empowers you to interpret and utilize numerical data effectively. So, remember: 17 out of 20 is 0.85 or 85% – but more importantly, understanding how to arrive at that answer is the key to unlocking a deeper understanding of mathematics and its practical applications.
Latest Posts
Latest Posts
-
What Does Cug Code For
Sep 22, 2025
-
How Many Feet Is 180
Sep 22, 2025
-
Themes For The Scarlet Ibis
Sep 22, 2025
-
Adjourning Stage In Group Development
Sep 22, 2025
-
18 Out Of 20 Percent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What's 17 Out Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.