18 Out Of 20 Percent
scising
Sep 22, 2025 · 5 min read
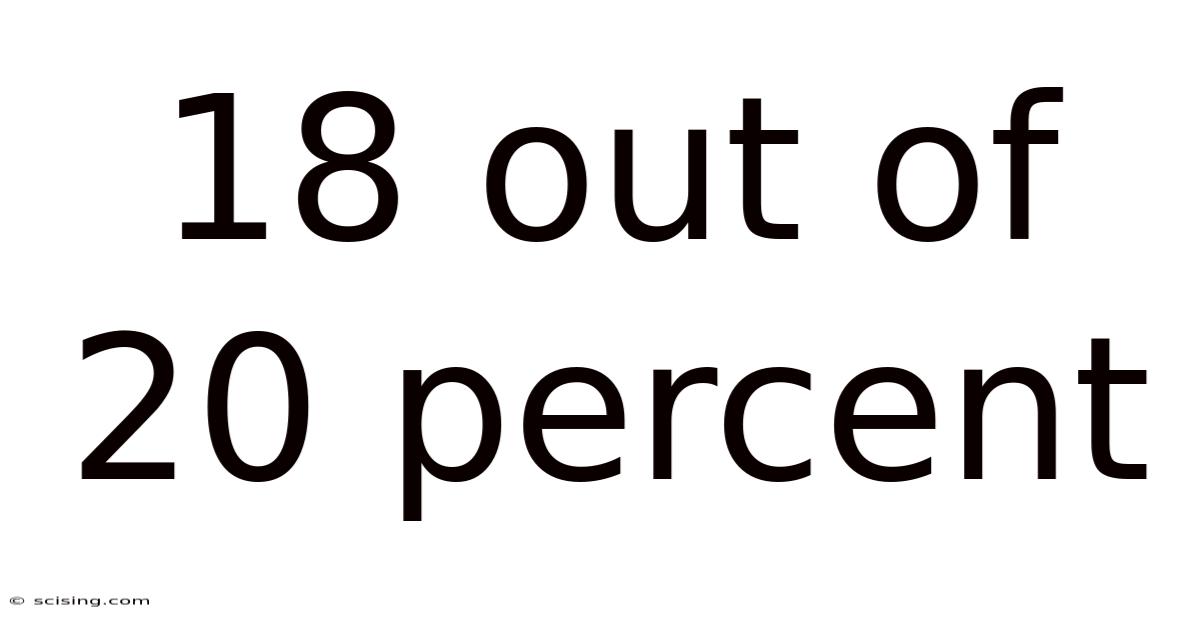
Table of Contents
Understanding 18 out of 20: Percentages, Fractions, and Real-World Applications
What does 18 out of 20 actually mean? This seemingly simple question opens the door to a deeper understanding of percentages, fractions, and their practical applications in everyday life. This article will not only explain how to calculate 18 out of 20 as a percentage and fraction but also delve into the broader concepts, providing you with a solid foundation in mathematical reasoning and problem-solving. We'll explore various real-world scenarios where this type of calculation is crucial and provide you with the tools to confidently tackle similar problems in the future.
Calculating 18 out of 20: The Basics
The phrase "18 out of 20" represents a part-to-whole relationship. It signifies that 18 represents a portion of a larger whole, which is 20 in this case. To express this relationship mathematically, we can use fractions and percentages.
1. Fraction:
The simplest way to express 18 out of 20 is as a fraction: 18/20. This fraction means 18 parts out of a total of 20 parts. We can simplify this fraction by finding the greatest common divisor (GCD) of 18 and 20, which is 2. Dividing both the numerator (18) and the denominator (20) by 2, we get the simplified fraction 9/10.
2. Percentage:
To express 18 out of 20 as a percentage, we first convert the fraction 18/20 to a decimal. We do this by dividing the numerator by the denominator: 18 ÷ 20 = 0.9. To convert this decimal to a percentage, we multiply by 100: 0.9 x 100 = 90%. Therefore, 18 out of 20 is equivalent to 90%.
In summary: 18 out of 20 can be expressed as the fraction 9/10 or the percentage 90%.
Understanding Percentages: A Deeper Dive
Percentages are a crucial tool for expressing proportions and comparing quantities. They represent a fraction out of 100, making them easy to understand and compare across different contexts. Let's explore some key aspects of percentages:
-
Calculating Percentages: To calculate a percentage, you divide the part by the whole and multiply by 100. The formula is: (Part/Whole) x 100 = Percentage.
-
Percentage Increase/Decrease: Percentages are frequently used to express changes in quantities. A percentage increase shows how much a value has grown, while a percentage decrease shows how much it has shrunk. The formulas are:
- Percentage Increase: [(New Value - Original Value) / Original Value] x 100
- Percentage Decrease: [(Original Value - New Value) / Original Value] x 100
-
Applications of Percentages: Percentages are ubiquitous in everyday life, including:
- Finance: Interest rates, discounts, taxes, investment returns.
- Statistics: Representing data in charts and graphs, analyzing survey results.
- Science: Expressing concentrations, efficiencies, and error margins.
- Everyday Life: Tips, sales, grades, and much more.
Real-World Applications of 18 out of 20 (or 90%)
Understanding how to calculate and interpret 18 out of 20, or its equivalent 90%, has numerous practical applications:
-
Academic Performance: If a student answers 18 out of 20 questions correctly on a test, they achieve a score of 90%. This is a high score, indicating a strong understanding of the subject matter.
-
Manufacturing Quality Control: In a factory producing 20 items, if 18 are defect-free, the production efficiency is 90%. This data helps identify areas for improvement in the manufacturing process.
-
Sales and Marketing: If a salesperson achieves 18 sales out of 20 targets, their success rate is 90%. This information is crucial for evaluating performance and setting future targets.
-
Sports Statistics: A basketball player making 18 out of 20 free throws demonstrates a 90% free-throw shooting percentage, which is exceptionally high.
-
Surveys and Polling: If 18 out of 20 respondents agree with a particular statement in a survey, the agreement rate is 90%. This provides valuable insight into public opinion.
Expanding the Understanding: Beyond 18 out of 20
While understanding 18 out of 20 is valuable, it's equally important to grasp the underlying principles of ratios, proportions, and percentages. This allows you to solve a wide range of similar problems:
-
Different Numerators and Denominators: You can apply the same methods to calculate percentages for other ratios, such as 15 out of 25, 12 out of 15, or any other part-to-whole relationship.
-
Working Backwards: If you know the percentage and the whole, you can calculate the part. For example, if you need to find 90% of 50, you would multiply 50 by 0.9 (or 90/100), resulting in 45.
-
Complex Scenarios: Real-world problems often involve multiple calculations. For example, calculating a discount on an item and then adding sales tax involves applying percentages in multiple steps.
Frequently Asked Questions (FAQs)
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100.
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction.
Q: What is the difference between a ratio and a percentage?
A: A ratio compares two quantities, while a percentage expresses a quantity as a fraction of 100. A percentage is a specific type of ratio.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare and represent proportions, facilitating easier understanding and communication across various fields.
Q: How can I improve my understanding of percentages?
A: Practice solving various percentage problems, both simple and complex. Use online resources, workbooks, or seek assistance from a tutor if needed.
Conclusion: Mastering Percentages for a Brighter Future
Understanding "18 out of 20," and more broadly, the concept of percentages, is fundamental to navigating the complexities of the modern world. From academic success to financial literacy, mastering percentages equips you with the essential tools for critical thinking and problem-solving. By grasping the underlying principles and applying them to real-world scenarios, you will not only improve your mathematical skills but also enhance your overall ability to analyze and interpret information effectively. Remember, consistent practice is key to mastering this essential mathematical concept and unlocking its vast potential in your personal and professional life. So, embrace the challenge, explore the applications, and watch your understanding blossom!
Latest Posts
Latest Posts
-
Black And White Optical Illusion
Sep 22, 2025
-
What Times What Equals 28
Sep 22, 2025
-
Historical Events In New Mexico
Sep 22, 2025
-
Meaning Of Transmission Of Light
Sep 22, 2025
-
Continent In All 4 Hemispheres
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 18 Out Of 20 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.