What Times What Equals 28
scising
Sep 22, 2025 · 5 min read
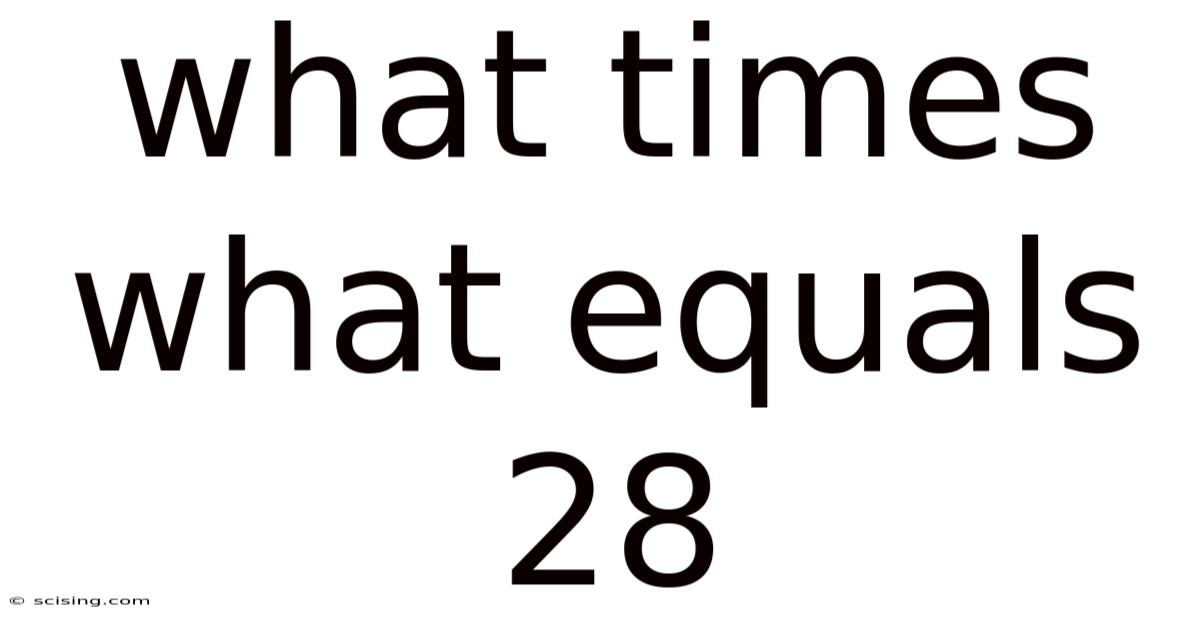
Table of Contents
What Times What Equals 28? Exploring the Factors and Applications of Multiplication
Finding the factors that multiply to equal 28 might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly basic question opens doors to a deeper understanding of number theory, multiplication, and its various applications in different fields. This article will explore the different pairs of numbers that multiply to 28, delve into the mathematical concepts involved, and demonstrate its relevance in various practical scenarios.
Understanding Factors and Multiples
Before diving into the solutions, let's clarify some fundamental mathematical terms. Factors are numbers that divide evenly into a given number without leaving a remainder. For instance, the factors of 28 are all the numbers that can be multiplied together to get 28. Conversely, multiples are the results of multiplying a number by integers (whole numbers). 28 is a multiple of 1, 2, 4, 7, 14, and 28.
Finding the Pairs: What Times What Equals 28?
The question "What times what equals 28?" seeks the pairs of factors of 28. Let's list them systematically:
- 1 x 28 = 28: This is the most straightforward pair. One multiplied by any number always results in that number.
- 2 x 14 = 28: This pair involves two even numbers.
- 4 x 7 = 28: This is another frequently used factor pair, involving both a small and a relatively larger number.
- 7 x 4 = 28: Note that the order of multiplication doesn't change the result. This demonstrates the commutative property of multiplication.
- 14 x 2 = 28: Again, the order is reversed, highlighting the commutative property.
- 28 x 1 = 28: This completes the set of factor pairs.
Therefore, the pairs of numbers that multiply to 28 are (1, 28), (2, 14), (4, 7), and their reversed counterparts. These pairs represent all possible integer solutions to the equation x * y = 28.
Beyond Integer Solutions: Exploring Rational and Real Numbers
While the above pairs represent all the integer solutions, the equation x * y = 28 has infinitely many solutions if we extend the possibilities beyond integers. We could consider rational numbers (fractions) or even real numbers (including irrational numbers). For example:
- 0.5 x 56 = 28: Here, we use a fraction (0.5 or 1/2).
- 2.8 x 10 = 28: Another example involving a decimal number.
And indeed, for every x, there exists a y such that x * y = 28, except when x = 0 (division by zero is undefined). This infinite range of solutions highlights the richness and complexity of mathematical equations.
Prime Factorization: Unveiling the Building Blocks of 28
The concept of prime factorization offers a deeper insight into the number 28. Prime factorization involves expressing a number as a product of its prime factors – numbers divisible only by 1 and themselves. The prime factorization of 28 is 2 x 2 x 7, or 2² x 7. This reveals the fundamental building blocks of the number 28. Understanding prime factorization is crucial in various areas of mathematics, including cryptography and number theory.
Practical Applications: Where Does This Matter?
The seemingly simple problem of finding factors of 28 has surprising relevance in diverse fields:
-
Geometry: Imagine calculating the area of a rectangle. If the area is 28 square units, the possible dimensions could be 1 unit by 28 units, 2 units by 14 units, or 4 units by 7 units. Understanding the factors helps determine possible dimensions.
-
Division Problems: Knowing the factors of 28 simplifies division problems. For example, dividing 28 objects into groups requires considering the factors to distribute them evenly.
-
Algebra: The equation x * y = 28 is a fundamental algebraic expression. Solving for x or y introduces the concepts of variables and equations, forming the basis of algebraic manipulation.
-
Combinatorics: In combinatorics, determining the number of ways to arrange or select items often involves finding factors and multiples. Consider arranging 28 items into rows; the number of rows depends on the factors of 28.
-
Computer Science: Factorization plays a significant role in cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring large numbers into their prime factors.
-
Real-World Scenarios: Consider arranging 28 chairs into rows for a meeting or dividing 28 cookies among friends. These simple tasks illustrate the practical utility of understanding factors.
Extending the Concept: Factors of Larger Numbers
The principles we've discussed for finding the factors of 28 extend to larger numbers. However, the process might become more complex. For larger numbers, techniques like prime factorization become even more important in identifying all possible factors efficiently. Specialized algorithms are used for factoring very large numbers in computer science and cryptography.
Frequently Asked Questions (FAQ)
Q: Are there any negative factors of 28?
A: Yes, if we consider negative integers, we also have pairs like (-1, -28), (-2, -14), (-4, -7). The product of two negative numbers is a positive number.
Q: How do I find factors of larger numbers quickly?
A: For larger numbers, prime factorization is the most efficient method. Break down the number into its prime factors, and then combine those factors in different ways to find all possible pairs.
Q: What if I need to find factors of a number that is not a whole number?
A: If you're working with non-integer numbers (decimals or fractions), the number of factors becomes infinite, as shown in the earlier examples with decimals.
Conclusion: The Significance of Simple Arithmetic
While the question "What times what equals 28?" appears simple, exploring its solutions provides a gateway to understanding fundamental mathematical concepts. From factors and multiples to prime factorization and its applications in various fields, this seemingly basic problem unveils a world of mathematical richness and practical relevance. The ability to identify factors and work with equations underpins many aspects of mathematics and its applications in the real world, demonstrating that even the simplest arithmetic can hold significant value. This exploration encourages us to appreciate the interconnectedness of mathematical ideas and their profound impact on our understanding of the world around us.
Latest Posts
Latest Posts
-
What Is Matris In English
Sep 22, 2025
-
Definition Of Rhythm In Art
Sep 22, 2025
-
Difference In Tone And Mood
Sep 22, 2025
-
Themes In The Glass Castle
Sep 22, 2025
-
Feudal Europe Vs Feudal Japan
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.