Whats 10 Percent Of 25
scising
Sep 19, 2025 · 5 min read
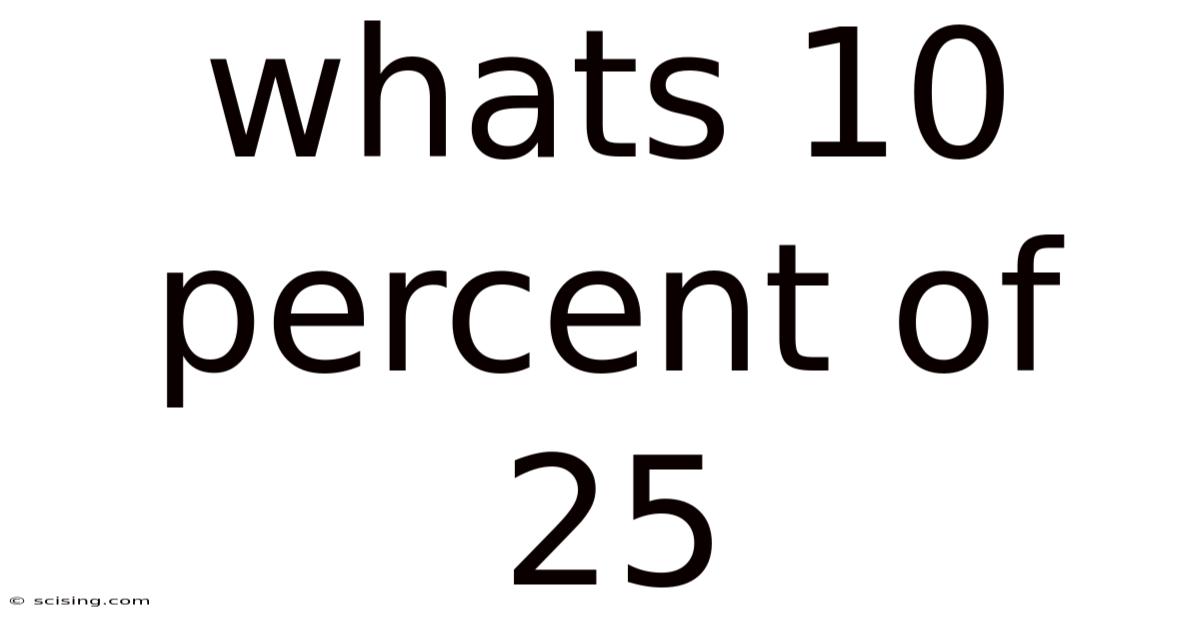
Table of Contents
What's 10 Percent of 25? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 25 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and more importantly, grasping the underlying concepts, is crucial for navigating everyday life, from budgeting and shopping to understanding financial reports and statistics. This article will not only answer the question "What's 10 percent of 25?" but will also delve into the broader context of percentages, exploring different methods of calculation, real-world applications, and frequently asked questions.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10 percent literally means 10 out of 100, or 10/100, which simplifies to 1/10. This fractional representation is key to understanding percentage calculations.
Method 1: The Fraction Method – Calculating 10% of 25
The simplest method to find 10% of 25 is to use the fractional equivalent. As established, 10% is equal to 1/10. To find 10% of 25, we simply multiply 25 by 1/10:
25 x (1/10) = 25/10 = 2.5
Therefore, 10% of 25 is 2.5.
Method 2: The Decimal Method – Calculating 10% of 25
Another common method involves converting the percentage to a decimal. To convert a percentage to a decimal, divide the percentage by 100. In this case:
10% ÷ 100 = 0.10 (or simply 0.1)
Now, multiply this decimal by the number you want to find the percentage of:
25 x 0.1 = 2.5
Again, we arrive at the answer: 10% of 25 is 2.5.
Method 3: The Proportion Method – A More Versatile Approach
The proportion method is a more versatile technique applicable to a wider range of percentage problems. It involves setting up a proportion:
Part/Whole = Percentage/100
In our case:
x/25 = 10/100
To solve for 'x' (which represents 10% of 25), we cross-multiply:
100x = 250
x = 250/100 = 2.5
Once again, we find that 10% of 25 is 2.5.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Sales Tax: Calculating the sales tax on a purchase requires finding a percentage of the original price. For example, if the sales tax is 6%, you would calculate 6% of the purchase price to determine the tax amount.
-
Discounts: Retailers often advertise discounts as percentages. If a store offers a 20% discount on an item, calculating 20% of the original price will determine the amount of the discount.
-
Tips: Calculating a tip in a restaurant involves finding a percentage of the bill amount. A common practice is to calculate 15% or 20% of the total bill.
-
Interest Rates: Understanding interest rates on loans or savings accounts requires a strong grasp of percentage calculations. Interest is typically calculated as a percentage of the principal amount.
-
Financial Statements: Financial statements such as income statements and balance sheets frequently use percentages to represent ratios and trends. For instance, profit margins are often expressed as a percentage of revenue.
-
Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions and probabilities. For example, polling data is often expressed in terms of percentages.
Beyond the Basics: Calculating Other Percentages of 25
While we've focused on 10%, let's quickly explore how to calculate other percentages of 25 using the decimal method:
- 25% of 25: 25 x 0.25 = 6.25
- 50% of 25: 25 x 0.50 = 12.5
- 75% of 25: 25 x 0.75 = 18.75
- 100% of 25: 25 x 1.00 = 25
Notice that 100% of any number is simply the number itself.
Understanding Percentage Increase and Decrease
Percentages are not only used to find a portion of a number, but also to represent increases and decreases.
-
Percentage Increase: To calculate a percentage increase, first find the difference between the new value and the original value. Then, divide this difference by the original value and multiply by 100 to express it as a percentage.
-
Percentage Decrease: This is calculated similarly. Find the difference between the original value and the new value (this difference will be negative). Then, divide this difference by the original value and multiply by 100. The result will be a negative percentage, indicating a decrease.
For example, if the price of an item increases from $20 to $25, the percentage increase is calculated as follows:
(25-20)/20 x 100 = 25%
Frequently Asked Questions (FAQ)
Q1: How do I calculate percentages quickly in my head?
A1: For some percentages, mental math tricks can be helpful. For example, 10% is easily calculated by moving the decimal point one place to the left. 50% is half the number, 25% is a quarter, and so on. Practice and familiarity with these basic percentages will improve your mental calculation skills.
Q2: What if I need to calculate a percentage that isn't a whole number, like 7.5%?
A2: You can use the same methods outlined above, simply converting the percentage to its decimal equivalent (7.5% = 0.075) and multiplying by the number.
Q3: Are there any online calculators or tools available to help with percentage calculations?
A3: Yes, numerous online percentage calculators are readily available. These tools can be helpful for quick calculations or for verifying your manual calculations.
Q4: Why is understanding percentages important in finance?
A4: Percentages are fundamental in finance for analyzing financial statements, calculating interest rates, evaluating investment returns, and making informed financial decisions. A strong understanding of percentages is crucial for managing personal finances and making sound investment choices.
Conclusion: Mastering Percentages for a Brighter Future
While the initial question, "What's 10 percent of 25?" may seem trivial, its answer opens the door to a much broader understanding of percentages and their far-reaching applications. From simple calculations to complex financial analyses, the ability to confidently work with percentages is a valuable skill that empowers individuals to navigate various aspects of life with greater understanding and competence. Mastering percentage calculations isn't just about getting the right numerical answer; it's about developing a crucial skillset applicable across diverse fields and scenarios, fostering financial literacy and enhancing problem-solving abilities. By understanding the underlying principles and employing the methods discussed in this article, you can confidently tackle any percentage-related challenge you may encounter.
Latest Posts
Latest Posts
-
How To Pronounce Carpe Diem
Sep 19, 2025
-
8 Qt How Many Cups
Sep 19, 2025
-
D Major Scale In Guitar
Sep 19, 2025
-
Whats 1 2 As A Fraction
Sep 19, 2025
-
How Long Is 25 Meters
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.