What's 1.2 As A Fraction
scising
Sep 19, 2025 · 5 min read
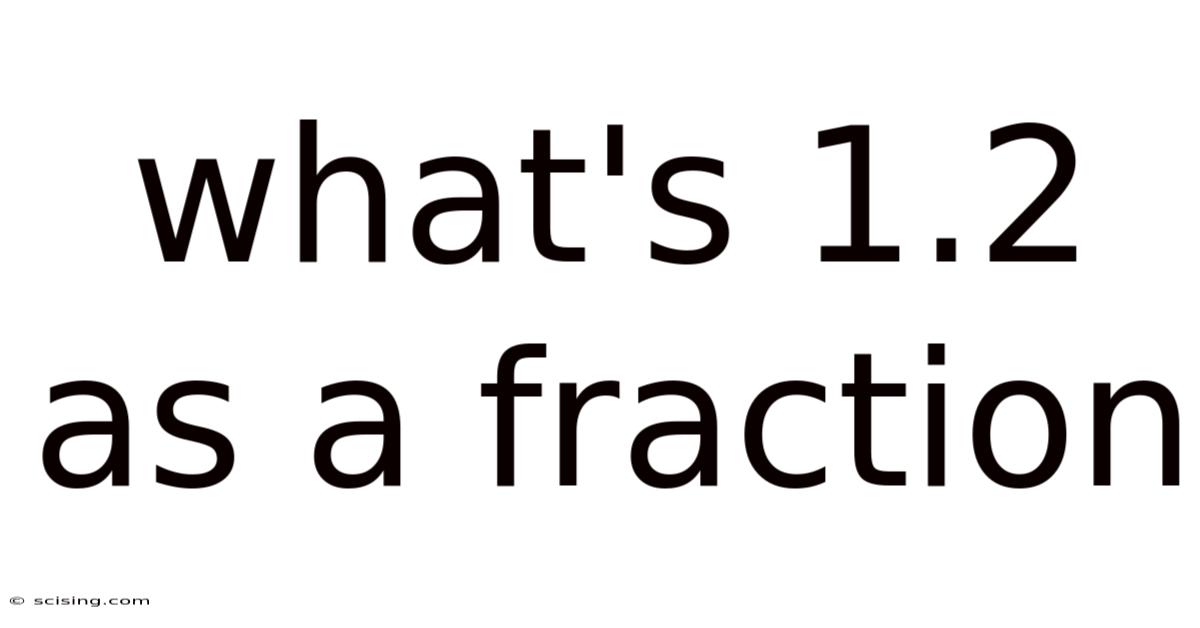
Table of Contents
What's 1.2 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 1.2 into a fraction but will also delve into the underlying principles, explore different methods, and address common questions surrounding decimal-to-fraction conversions. This will equip you with a strong understanding of this crucial mathematical concept.
Understanding Decimals and Fractions
Before we dive into converting 1.2, let's quickly review the basics of decimals and fractions. A decimal is a way of expressing a number using a base-ten system, where the digits to the right of the decimal point represent fractions with denominators that are powers of 10 (10, 100, 1000, etc.). A fraction, on the other hand, represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number).
Converting 1.2 to a Fraction: The Simple Method
The simplest way to convert 1.2 to a fraction involves understanding the place value of the digits. The number 1.2 can be broken down as follows:
- 1: Represents one whole unit.
- .2: Represents two-tenths (2/10).
Therefore, 1.2 can be written as the sum of these two parts: 1 + 2/10. This can be simplified further by converting the whole number 1 into a fraction with the same denominator as 2/10, which is 10/10. Adding these fractions together, we get:
10/10 + 2/10 = 12/10
This fraction, 12/10, is an improper fraction because the numerator (12) is larger than the denominator (10).
Simplifying the Fraction
Improper fractions are often simplified to mixed numbers or further reduced to their simplest form. A mixed number combines a whole number and a proper fraction (numerator smaller than the denominator). To simplify 12/10:
-
Find the Greatest Common Divisor (GCD): The GCD of 12 and 10 is 2. This means both numbers can be divided by 2 without leaving a remainder.
-
Divide both the numerator and the denominator by the GCD:
12 ÷ 2 = 6 10 ÷ 2 = 5
Therefore, the simplified fraction is 6/5.
This is still an improper fraction. To express it as a mixed number, we divide the numerator (6) by the denominator (5):
6 ÷ 5 = 1 with a remainder of 1.
This means 6/5 is equivalent to 1 and 1/5. Therefore, 1.2 as a fraction can be expressed as 6/5 or 1 1/5.
Alternative Method: Using the Power of 10
Another approach involves directly utilizing the powers of 10 inherent in the decimal system. Since 1.2 has one digit after the decimal point, we can multiply both the numerator and denominator by 10¹ (which is 10):
1.2 = 1.2/1
Multiplying the numerator and denominator by 10:
(1.2 x 10) / (1 x 10) = 12/10
This leads us back to the same improper fraction, 12/10, which, as shown previously, simplifies to 6/5 or 1 1/5.
Converting Other Decimals to Fractions
The methods described above can be applied to convert other decimals to fractions. Let's look at a few examples:
- 0.75: This decimal has two digits after the decimal point, so we multiply the numerator and denominator by 10² (100):
(0.75 x 100) / (1 x 100) = 75/100. This simplifies to 3/4.
- 2.3: This decimal has one digit after the decimal point, so we multiply by 10:
(2.3 x 10) / (1 x 10) = 23/10. This is an improper fraction and can be expressed as the mixed number 2 3/10.
- 0.005: This decimal has three digits after the decimal point, so we multiply by 10³ (1000):
(0.005 x 1000) / (1 x 1000) = 5/1000. This simplifies to 1/200.
The Importance of Simplification
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and work with.
- Efficiency: Simplified fractions make calculations simpler and faster.
- Standardization: Expressing fractions in their simplest form ensures consistency in mathematical representations.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, use in calculations, and compare to other fractions. It ensures a standard and efficient representation of the numerical value.
Q2: Can I leave my answer as an improper fraction?
A2: While technically correct, improper fractions are often converted to mixed numbers for better readability and easier understanding, especially in practical applications. The context often dictates the preferred format.
Q3: What if I have a repeating decimal?
A3: Converting repeating decimals to fractions requires a slightly different approach that involves algebraic manipulation. It's a more advanced concept that goes beyond the scope of this basic guide, but there are many resources available online that explain this process in detail.
Q4: What if the decimal has more than one digit before the decimal point?
A4: Treat the whole number part separately. Convert the decimal part to a fraction using the methods explained above, then add the whole number. For example, 3.75 becomes 3 + 75/100 = 3 + 3/4 = 15/4.
Conclusion
Converting decimals to fractions is a fundamental mathematical skill with broad applications. The process, while seemingly simple for numbers like 1.2, highlights the interconnectedness of different numerical representations. By understanding the principles of place value, greatest common divisors, and simplification, you can confidently convert any decimal to its equivalent fraction. Remember the steps: identify the place value, write it as a fraction, then simplify to its lowest terms. Mastering this skill will significantly enhance your mathematical fluency and problem-solving abilities. Remember, practice makes perfect! The more you work through examples, the easier it will become.
Latest Posts
Latest Posts
-
Largest Tiger In The World
Sep 19, 2025
-
Watching A Movie In Spanish
Sep 19, 2025
-
Is Pi Rational Or Irrational
Sep 19, 2025
-
Legato Symbol On A Score
Sep 19, 2025
-
Can Teachers Physically Discipline Students
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What's 1.2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.