Whats 10 Percent Of 15
scising
Sep 10, 2025 · 5 min read
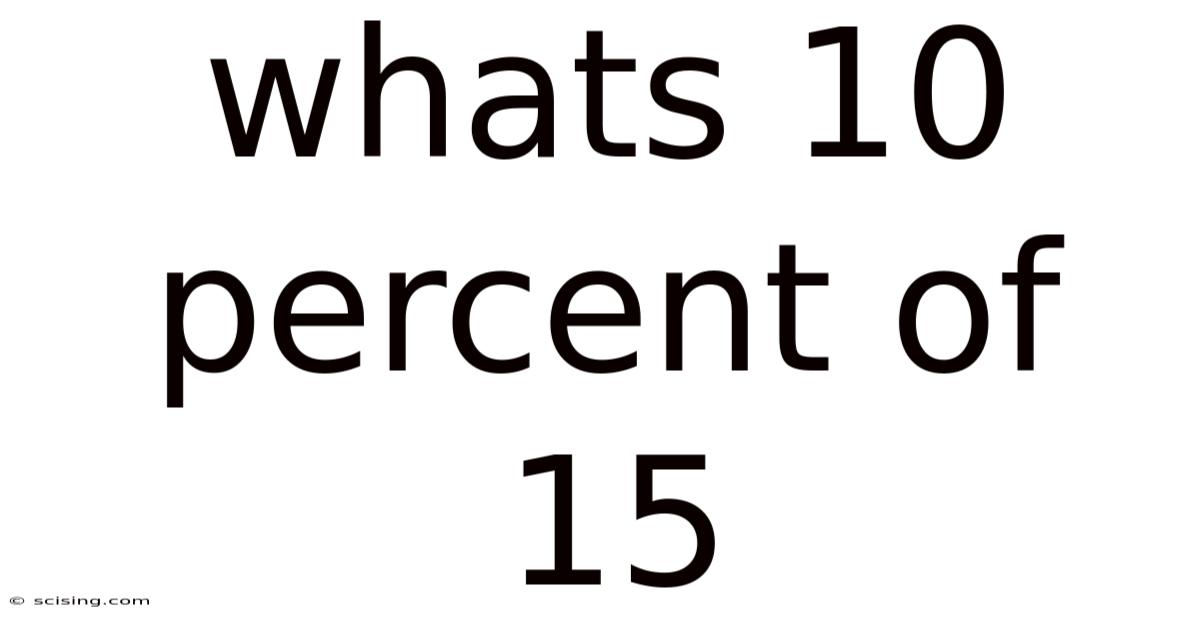
Table of Contents
What's 10 Percent of 15? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 15 might seem like a simple calculation, a quick mental math problem. But understanding how to arrive at that answer, and more importantly, grasping the underlying concepts of percentages, opens up a world of practical applications in everyday life, from budgeting and shopping to understanding financial reports and scientific data. This article will not only answer the question "What's 10 percent of 15?" but will also explore the broader topic of percentages, providing you with the tools to confidently tackle similar calculations and understand their significance.
Understanding Percentages: The Building Blocks
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." So, 10 percent (written as 10%) means 10 out of 100, or 10/100. This can be simplified to 1/10. Understanding this fundamental concept is key to solving any percentage problem.
Calculating 10 Percent of 15: Three Methods
There are several ways to calculate 10 percent of 15. Let's explore three common methods:
Method 1: Using the Fraction Method
As we established, 10% is equivalent to 1/10. To find 10% of 15, we simply multiply 15 by 1/10:
15 x (1/10) = 15/10 = 1.5
Therefore, 10 percent of 15 is $\boxed{1.5}$
Method 2: Using Decimal Conversion
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. For 10%, this is:
10 / 100 = 0.1
Now, multiply this decimal by 15:
15 x 0.1 = 1.5
Again, we find that 10 percent of 15 is $\boxed{1.5}$
Method 3: Using the Proportion Method
This method is particularly useful for more complex percentage problems. We set up a proportion:
10/100 = x/15
Here, 'x' represents the unknown value (10% of 15). To solve for 'x', we cross-multiply:
10 * 15 = 100 * x
150 = 100x
x = 150/100 = 1.5
Once more, we arrive at the answer: 10 percent of 15 is $\boxed{1.5}$
Beyond the Basics: Calculating Other Percentages
While finding 10% is straightforward, understanding the methods above allows you to calculate any percentage of any number. Let's look at some examples:
- Finding 25% of 15: 25% = 0.25. Therefore, 15 x 0.25 = 3.75
- Finding 5% of 15: 5% = 0.05. Therefore, 15 x 0.05 = 0.75
- Finding 15% of 20: 15% = 0.15. Therefore, 20 x 0.15 = 3
- Finding x% of y: The general formula is (x/100) * y
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in everyday life. Here are some examples:
- Sales and Discounts: Stores frequently advertise discounts as percentages (e.g., "20% off"). Understanding percentages allows you to quickly calculate the actual savings.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages.
- Tips and Gratuities: Calculating tips in restaurants usually involves finding a percentage of the bill.
- Interest Rates: Interest on loans, savings accounts, and credit cards is expressed as a percentage.
- Financial Statements: Financial reports, such as balance sheets and income statements, use percentages extensively to present data in a meaningful way.
- Scientific Data: Percentages are widely used in scientific research to represent proportions and changes in data.
- Surveys and Polls: Results from surveys and polls are often presented as percentages.
Understanding Percentage Increase and Decrease
Beyond finding a percentage of a number, it's crucial to understand percentage increase and decrease.
- Percentage Increase: This calculates the percentage change when a value increases. The formula is: [(New Value - Original Value) / Original Value] x 100%.
For example, if a price increases from $10 to $12, the percentage increase is [(12-10)/10] x 100% = 20%.
- Percentage Decrease: This calculates the percentage change when a value decreases. The formula is: [(Original Value - New Value) / Original Value] x 100%.
For example, if a price decreases from $20 to $15, the percentage decrease is [(20-15)/20] x 100% = 25%.
Troubleshooting Common Percentage Calculation Mistakes
Several common errors can occur when working with percentages:
- Incorrect Decimal Conversion: Failing to correctly convert percentages to decimals is a frequent mistake. Remember to divide the percentage by 100.
- Misunderstanding the "of" in "x% of y": The word "of" always signifies multiplication.
- Confusing Percentage Increase and Decrease: Make sure you understand the correct formulas for calculating percentage changes.
- Rounding Errors: Be mindful of rounding errors, especially in complex calculations. Try to avoid rounding until the final answer.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on the specific percentage and your comfort level with different approaches. For 10%, the fraction method is often quickest. For other percentages, the decimal conversion method is generally straightforward.
Q: How can I improve my percentage calculation skills?
A: Practice is key! Work through various examples, starting with simpler problems and gradually increasing the complexity. Use different methods to solve the same problem to build your understanding.
Q: Are there any online tools or calculators that can help me with percentages?
A: Yes, numerous online percentage calculators are available. These can be helpful for checking your work or for solving more complex percentage problems.
Conclusion: Mastering Percentages – A Lifelong Skill
Understanding percentages is a fundamental skill applicable across numerous aspects of life. While finding 10 percent of 15 might seem trivial at first glance, mastering the underlying principles empowers you to confidently tackle a wide range of quantitative problems, from managing your finances to interpreting data in various fields. By employing the methods discussed in this article and practicing regularly, you can build a strong foundation in percentage calculations, opening doors to greater understanding and success in your academic and professional endeavors. Remember that consistent practice and a clear understanding of the underlying concepts are the keys to mastering percentages and applying them effectively in various contexts.
Latest Posts
Latest Posts
-
Whats 20 Percent Of 18
Sep 10, 2025
-
Map Of Maya Inca Aztec
Sep 10, 2025
-
Is Co Polar Or Nonpolar
Sep 10, 2025
-
What Are The Concurrent Powers
Sep 10, 2025
-
Sensory Memory Ap Psychology Definition
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.