Whats 20 Percent Of 18
scising
Sep 10, 2025 · 6 min read
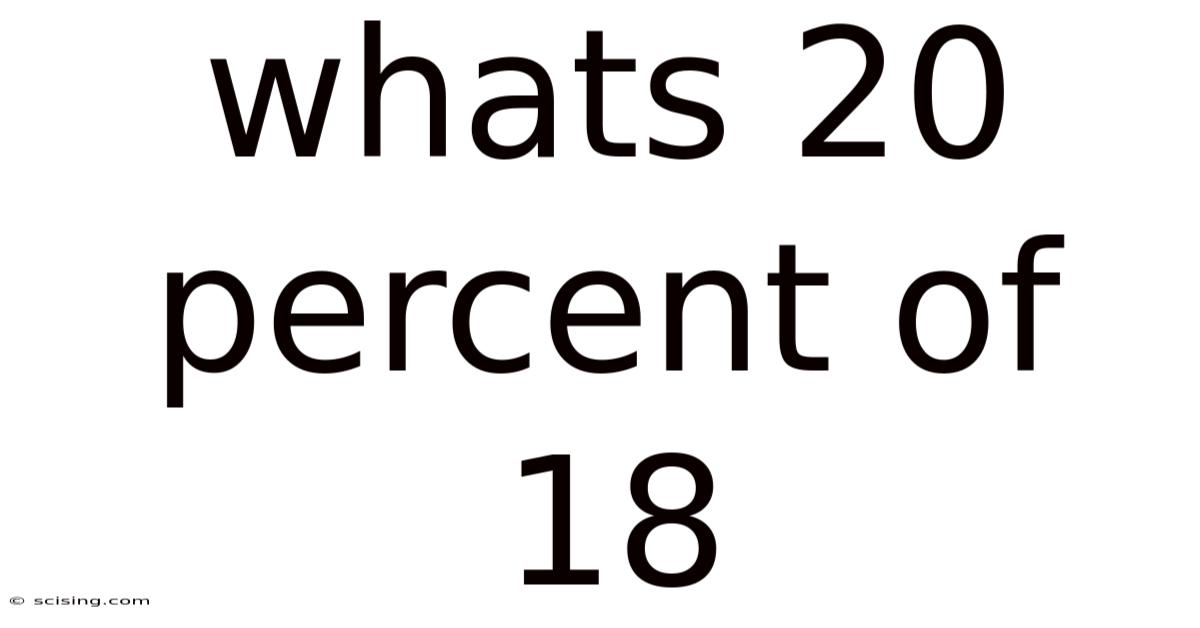
Table of Contents
What's 20 Percent of 18? A Deep Dive into Percentages and Practical Applications
Finding 20 percent of 18 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and sales tax to understanding financial statements and statistical data. This article will not only answer the question "What's 20 percent of 18?" but also explore the different methods for calculating percentages, explain the underlying mathematical concepts, and provide real-world examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). So, 20 percent means 20 out of 100, or 20/100, which simplifies to 1/5. This fundamental understanding is crucial for all percentage calculations.
Method 1: The Fraction Method
This is perhaps the most intuitive method, especially for smaller numbers. We know that 20% is equivalent to 20/100. To find 20% of 18, we simply multiply 18 by the fraction 20/100:
18 x (20/100) = 18 x (1/5) = 3.6
Therefore, 20% of 18 is 3.6.
This method clearly demonstrates the concept of "part of a whole". We're taking a fraction (20/100 or 1/5) of the whole number (18).
Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then multiplying. To convert a percentage to a decimal, we divide by 100 (or move the decimal point two places to the left). Thus, 20% becomes 0.20 or simply 0.2.
Now we multiply 18 by 0.2:
18 x 0.2 = 3.6
Again, we arrive at the answer: 3.6. This method is often preferred for larger numbers or when using calculators, as it's quicker and less prone to errors.
Method 3: The Proportion Method
This method is excellent for understanding the underlying relationship between percentages and proportions. We can set up a proportion:
x / 18 = 20 / 100
Where 'x' represents the unknown value (20% of 18). To solve for x, we cross-multiply:
100x = 18 * 20
100x = 360
x = 360 / 100
x = 3.6
The proportion method emphasizes the equivalence between ratios. It showcases how a percentage is simply a specific ratio expressed out of 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in a multitude of everyday situations:
-
Shopping: Calculating discounts is a prime example. If a $30 item is on sale for 20% off, you would calculate 20% of $30 (which is $6) and subtract that from the original price ($30 - $6 = $24).
-
Taxes: Sales tax is added to the price of goods and services. If the sales tax in your area is 6%, you'd calculate 6% of the item's price and add it to the original cost.
-
Finance: Interest rates on loans and investments are expressed as percentages. Understanding compound interest requires a strong grasp of percentage calculations. Calculating the interest earned on a savings account or the interest paid on a loan necessitates a thorough understanding of percentages.
-
Statistics: Percentages are ubiquitous in statistics, used to represent proportions within data sets. For instance, understanding survey results often involves interpreting percentages to draw conclusions.
-
Science: Many scientific calculations involve percentages, for example expressing the concentration of a solution or the efficiency of a process.
-
Everyday Life: Percentage calculations help us understand tips in restaurants (15% of the bill), the percentage of nutrients in food, or even the completion progress of a project.
Expanding the Understanding: Working with Different Percentages
While we've focused on 20%, the methods described apply to any percentage. Let's explore calculating other percentages of 18:
-
10% of 18: Using the decimal method, 10% is 0.1, so 18 x 0.1 = 1.8
-
50% of 18: This is half of 18, which is 9. Using the fraction method, 50/100 simplifies to 1/2, so 18 x (1/2) = 9
-
75% of 18: This is three-quarters of 18. Using the fraction method, 75/100 simplifies to 3/4, so 18 x (3/4) = 13.5
-
1% of 18: Using the decimal method, 1% is 0.01, so 18 x 0.01 = 0.18
Advanced Applications: Compound Interest and Growth Rates
Percentage calculations form the basis of many financial concepts, such as compound interest. Compound interest is interest earned on both the principal amount and accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding this formula, and how percentages are applied within it, is crucial for making informed financial decisions. Similarly, concepts such as population growth rates, economic growth, or inflation rates all rely heavily on percentage calculations.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The decimal method is often the quickest and easiest, especially for calculations involving a calculator. Converting the percentage to a decimal and multiplying is straightforward.
Q: Can I use a calculator for percentage calculations?
A: Absolutely! Calculators are very helpful, particularly for more complex percentage calculations or larger numbers. Most calculators have a percentage button (%) that simplifies the process.
Q: What if I need to find what percentage one number is of another?
A: To find what percentage number A is of number B, you divide A by B and multiply the result by 100. For example, to find what percentage 3 is of 15, you would calculate (3/15) * 100 = 20%.
Q: Are there any online resources or tools to help with percentage calculations?
A: Yes, many online calculators and websites are available to perform percentage calculations quickly and accurately. However, understanding the underlying principles is crucial for applying percentage calculations effectively in various contexts.
Conclusion
Calculating 20% of 18, resulting in 3.6, is a seemingly simple arithmetic operation. However, delving deeper reveals the fundamental importance of percentages in our daily lives and across numerous fields. Mastering the different methods of calculating percentages – the fraction method, decimal method, and proportion method – empowers you to tackle a vast range of practical problems, from budgeting and shopping to understanding financial concepts and interpreting statistical data. The ability to confidently work with percentages is a valuable skill that enhances your understanding of the world around you and equips you to make informed decisions in various aspects of life.
Latest Posts
Latest Posts
-
What Does Nos Vemos Mean
Sep 10, 2025
-
The Open Window By Saki
Sep 10, 2025
-
What Is A Tabloid Paper
Sep 10, 2025
-
Single Member District Example Ap Gov
Sep 10, 2025
-
What Is A Free Morpheme
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.