Square Root Of 150 Simplified
scising
Sep 18, 2025 · 5 min read
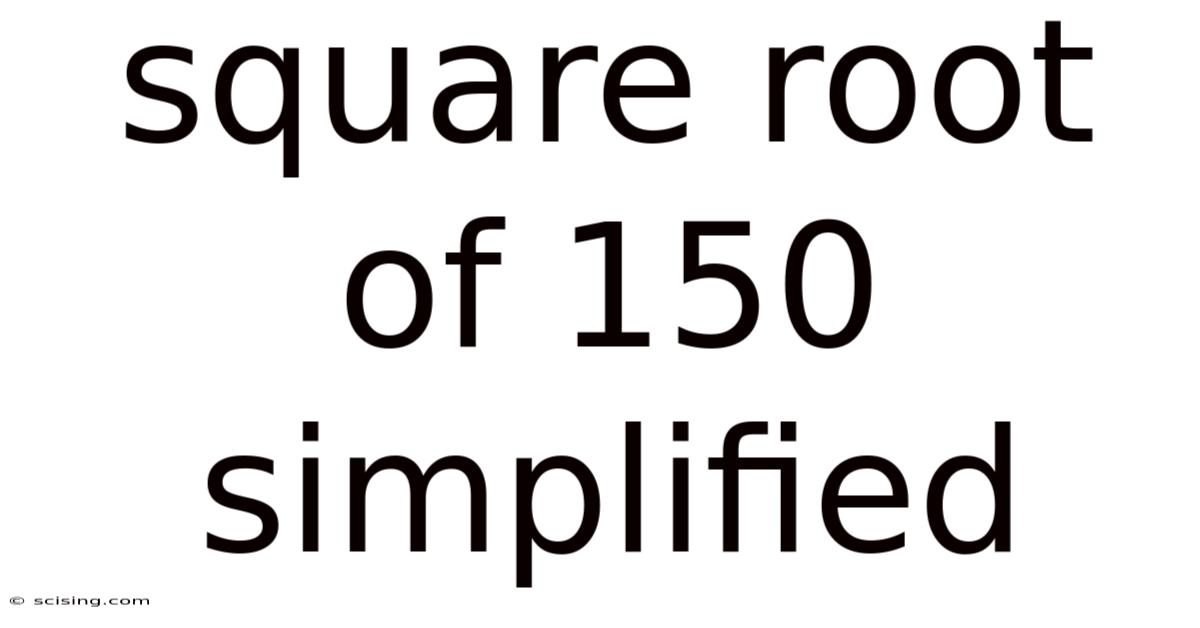
Table of Contents
Simplifying the Square Root of 150: A Comprehensive Guide
Finding the square root of 150 might seem like a straightforward task, especially with the aid of calculators. However, understanding the process of simplifying square roots, particularly one like √150, is crucial for developing a deeper understanding of number theory and algebraic manipulation. This comprehensive guide will walk you through the steps of simplifying √150, exploring the underlying mathematical principles, and answering frequently asked questions. We'll delve into the concept of prime factorization, a cornerstone technique for simplifying radicals. By the end, you'll not only know the simplified form of √150 but also possess the skills to simplify other square roots effectively.
Understanding Square Roots and Simplification
A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, not all square roots result in whole numbers. Numbers like √150 are irrational numbers, meaning their decimal representation continues indefinitely without repeating. This is where simplification comes in. Simplifying a square root means expressing it in its most concise form, often involving a whole number multiplied by a remaining square root.
Prime Factorization: The Key to Simplification
The process of simplifying square roots hinges on prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). To simplify √150, we begin by finding its prime factorization.
- Start with the smallest prime number, 2: 150 is an even number, so it's divisible by 2. 150 ÷ 2 = 75.
- Continue with the next prime number, 3: 75 is divisible by 3. 75 ÷ 3 = 25.
- Next prime number, 5: 25 is divisible by 5. 25 ÷ 5 = 5.
- We've reached another prime number, 5: 5 is a prime number, and the factorization is complete.
Therefore, the prime factorization of 150 is 2 x 3 x 5 x 5, or 2 x 3 x 5².
Simplifying √150 Step-by-Step
Now that we have the prime factorization (2 x 3 x 5²), we can simplify √150:
- Rewrite the square root using the prime factors: √(2 x 3 x 5²)
- Separate the perfect square: We can rewrite the expression as √(5²) x √(2 x 3)
- Simplify the perfect square: The square root of 5² is simply 5.
- Combine the remaining factors: The remaining factors, 2 and 3, are multiplied together under the square root sign.
Therefore, the simplified form of √150 is 5√6.
Visualizing the Simplification
Imagine a square with an area of 150 square units. We're trying to find the length of one side of this square. By factoring 150 into its prime factors (2 x 3 x 5 x 5), we can visualize this square as being composed of smaller squares. One of these smaller squares has sides of length 5 (5 x 5 = 25), and this represents the perfect square we extracted (5²). The remaining area (2 x 3 = 6) represents the remaining square root (√6). Thus, we have a larger square composed of a 5 x 5 square and an additional square with an area of 6 square units, leading to the simplified form of 5√6.
Working with Other Square Roots: A Practical Approach
The process demonstrated for simplifying √150 is applicable to other square roots. Here’s a step-by-step approach you can apply to any square root simplification problem:
- Find the prime factorization of the number under the square root.
- Identify any perfect squares within the prime factorization (pairs of identical prime factors).
- Take the square root of each perfect square (remove them from under the radical).
- Multiply the whole numbers obtained from the perfect squares.
- Multiply the remaining prime factors under the square root symbol.
- The result is the simplified form of the square root.
For example, let's simplify √72:
- Prime factorization of 72: 2³ x 3²
- Perfect squares: 2² and 3²
- Square roots of perfect squares: √2² = 2 and √3² = 3
- Multiply whole numbers: 2 x 3 = 6
- Remaining factors under the square root: √2
- Simplified form: 6√2
Frequently Asked Questions (FAQ)
Q1: Why is simplifying square roots important?
A1: Simplifying square roots makes mathematical expressions more concise and easier to work with. It’s essential for further algebraic manipulations and comparisons. Unsimplified square roots can be cumbersome in calculations and make it harder to identify relationships between numbers.
Q2: Can I use a calculator to simplify square roots?
A2: While calculators can give you a decimal approximation of a square root, they don't provide the simplified radical form. Understanding the simplification process is crucial for developing a deeper mathematical understanding and for handling problems where a decimal approximation isn't sufficient.
Q3: What if the number under the square root is negative?
A3: The square root of a negative number is an imaginary number, represented by the symbol i, where i² = -1. Simplifying these involves understanding complex numbers, a topic beyond the scope of this basic simplification guide.
Q4: Are there any shortcuts for simplifying larger square roots?
A4: While there aren't any significant shortcuts, familiarity with perfect squares (4, 9, 16, 25, 36, 49, 64, 81, 100, etc.) can significantly speed up the process. Recognizing these perfect squares within the prime factorization will help you quickly identify and extract them.
Conclusion
Simplifying square roots, like √150, is a fundamental skill in mathematics. Mastering this process strengthens your understanding of number theory, prime factorization, and algebraic manipulation. By following the step-by-step guide outlined above and practicing with various examples, you'll gain confidence in simplifying square roots and handling more complex mathematical problems effectively. Remember, the key lies in understanding the concept of prime factorization and efficiently identifying perfect squares within the factorization. The ability to simplify square roots is not just about finding the answer; it's about understanding the underlying mathematical principles and building a stronger foundation for your mathematical journey. Through consistent practice and a deeper understanding of the process, you'll find that simplifying square roots becomes increasingly intuitive and efficient.
Latest Posts
Latest Posts
-
How To Calculate Effective Interest
Sep 18, 2025
-
Nursing Diagnosis Related To Infection
Sep 18, 2025
-
What Is 7 Of 300
Sep 18, 2025
-
What Is Kmt In Chemistry
Sep 18, 2025
-
3 5 As A Percentage
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 150 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.