3 5 As A Percentage
scising
Sep 18, 2025 · 5 min read
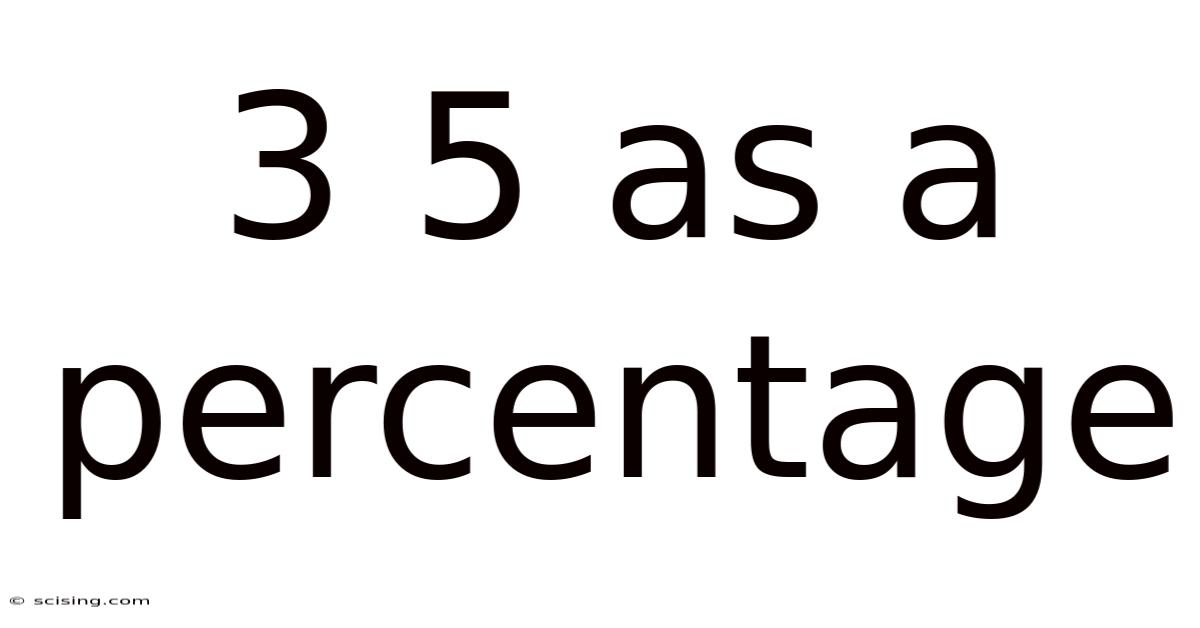
Table of Contents
Understanding 3/5 as a Percentage: A Comprehensive Guide
Representing fractions as percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and interest rates to understanding statistics and data analysis. This comprehensive guide will delve into the intricacies of converting the fraction 3/5 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We will cover different approaches, address common misconceptions, and equip you with the knowledge to confidently tackle similar conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion of 3/5 to a percentage, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 3/5 means we have 3 parts out of a total of 5 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion as a number out of 100. For example, 50% means 50 out of 100, which simplifies to 1/2. Percentages are a convenient way to express proportions, especially when comparing different quantities.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 3/5 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (5). 3 ÷ 5 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.6 x 100 = 60%.
Therefore, 3/5 is equal to 60%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method relies on the understanding that a percentage is a fraction with a denominator of 100. We can achieve this by finding an equivalent fraction of 3/5 that has a denominator of 100.
-
Determine the scaling factor: To change the denominator from 5 to 100, we need to multiply it by 20 (100 ÷ 5 = 20).
-
Apply the scaling factor to both the numerator and denominator: Multiply both the numerator and the denominator of 3/5 by 20: (3 x 20) / (5 x 20) = 60/100
-
Express as a percentage: Since 60/100 means 60 out of 100, it's equivalent to 60%.
Method 3: Using Proportions
Proportions offer another elegant way to solve this conversion problem. We can set up a proportion to find the equivalent percentage:
3/5 = x/100
Where 'x' represents the percentage we are trying to find.
To solve for 'x', we can cross-multiply:
5x = 300
Divide both sides by 5:
x = 60
Therefore, 3/5 is equal to 60%.
Illustrative Examples: Real-World Applications
Understanding the conversion of fractions to percentages is crucial in various real-world scenarios. Let's consider a few examples:
-
Discount Calculations: A store offers a 3/5 discount on an item. This means the discount is 60% of the original price.
-
Grade Calculation: If you answered 3 out of 5 questions correctly on a quiz, your score is 60%.
-
Data Analysis: If 3 out of 5 people surveyed preferred a certain product, this represents a 60% preference rate.
-
Financial Investments: If you invested in a project and earned 3 out of every 5 dollars invested, your return on investment is 60%.
Common Misconceptions and Pitfalls
While the conversion process is relatively straightforward, some common misconceptions can lead to errors:
-
Incorrect decimal placement: Carefully execute the division step when converting the fraction to a decimal. A misplaced decimal point will lead to an incorrect percentage.
-
Forgetting to multiply by 100: Remember to multiply the decimal by 100 to express it as a percentage. This is a crucial step often overlooked.
-
Confusion with other mathematical operations: Ensure you are performing the correct operations: division to convert to decimal and multiplication to convert to percentage.
Further Exploration: Working with More Complex Fractions
The methods discussed above can be applied to convert any fraction to a percentage. For instance, let's consider the fraction 7/8:
-
Convert to decimal: 7 ÷ 8 = 0.875
-
Convert to percentage: 0.875 x 100 = 87.5%
Therefore, 7/8 is equal to 87.5%.
Similarly, for fractions like 11/16:
-
Convert to decimal: 11 ÷ 16 = 0.6875
-
Convert to percentage: 0.6875 x 100 = 68.75%
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand fraction to percentage conversion?
A1: This conversion is essential for understanding proportions, comparing quantities, analyzing data, and solving problems across various fields, including finance, science, and everyday life.
Q2: Can I convert any fraction to a percentage?
A2: Yes, any fraction, proper or improper, can be converted to a percentage using the methods described above.
Q3: What if the decimal representation of a fraction is non-terminating?
A3: For non-terminating decimals, you can round the decimal to a desired number of decimal places before converting to a percentage. The accuracy of the percentage will depend on the level of rounding.
Q4: Are there any online calculators to help with this conversion?
A4: While there are many online calculators available, understanding the underlying principles is more beneficial for long-term learning and problem-solving skills.
Q5: Is there a difference between converting a proper fraction and an improper fraction to a percentage?
A5: The process remains the same for both proper and improper fractions. An improper fraction (where the numerator is greater than or equal to the denominator) will always result in a percentage greater than or equal to 100%.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental skill with widespread applications. Through the various methods outlined—direct conversion, equivalent fractions, and proportions—we have explored different approaches to solve this problem. By understanding these methods and avoiding common pitfalls, you can confidently tackle fraction-to-percentage conversions and apply this knowledge to solve real-world problems. Remember to practice regularly to solidify your understanding and build your mathematical skills. The ability to seamlessly convert fractions to percentages is a valuable asset that will serve you well throughout your academic and professional life.
Latest Posts
Latest Posts
-
El Dorado Chel Original Design
Sep 18, 2025
-
What Was 6 Days Ago
Sep 18, 2025
-
Is Chemistry A Physical Science
Sep 18, 2025
-
Samuel Of The Bible Facts
Sep 18, 2025
-
How To Evaluate A Logarithm
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.