Root 3 Times Root 3
scising
Sep 10, 2025 · 5 min read
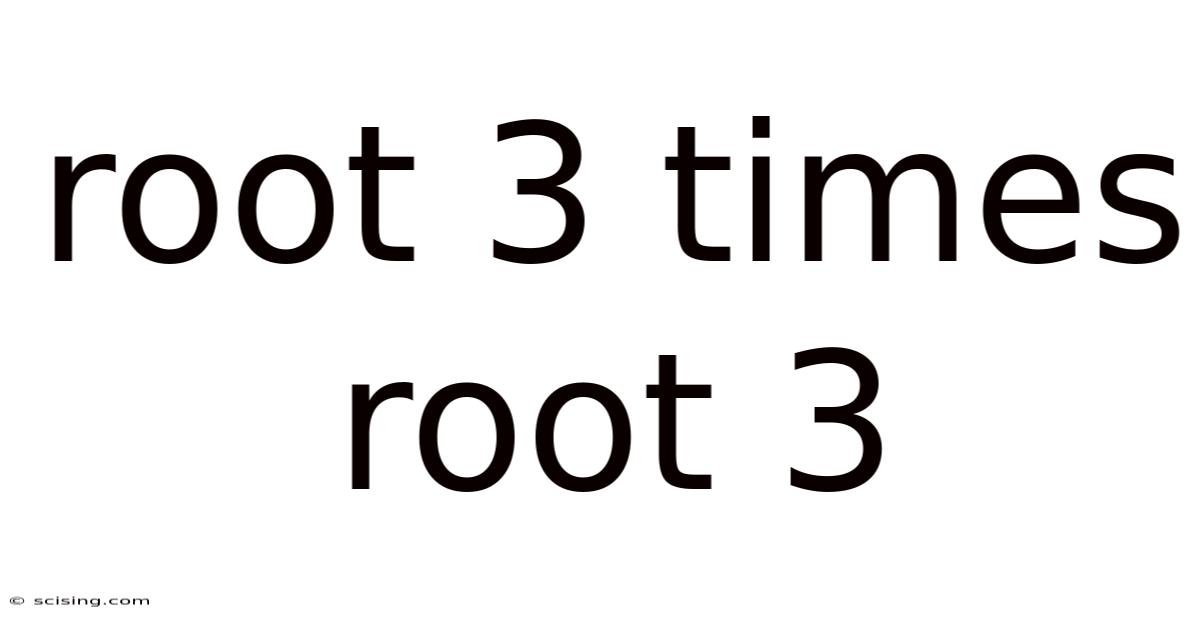
Table of Contents
Unveiling the Mystery: √3 x √3 and the Wonders of Radicals
Understanding the seemingly simple equation √3 x √3 is a gateway to comprehending more complex concepts in mathematics, particularly in the realm of radicals and exponents. This article delves deep into this seemingly basic calculation, exploring its solution, the underlying mathematical principles, and its implications in various mathematical applications. We’ll journey from the fundamental rules of radicals to more advanced concepts, ensuring a comprehensive understanding for readers of all mathematical backgrounds.
Introduction: Deconstructing the Problem
At first glance, √3 x √3 appears straightforward. However, a true understanding requires delving into the definition of square roots and their properties. The symbol '√' represents the principal square root, which is the non-negative number that, when multiplied by itself, yields the radicand (the number inside the square root symbol). Therefore, we're essentially asking: "What number, when multiplied by itself, equals 3?" The answer is not immediately obvious but can be elegantly derived using the rules of radicals and exponents.
Understanding Square Roots and Radicals
Before diving into the solution, let's solidify our understanding of radicals. A radical expression is an expression containing a radical symbol (√). The number inside the radical symbol is called the radicand, and the small number above the radical symbol (often omitted if it's 2, representing a square root) is called the index. For example, in √3, 3 is the radicand, and 2 is the implied index.
A square root is a radical with an index of 2. It asks the question: "What number, when multiplied by itself, gives the radicand?" For instance, √9 = 3 because 3 x 3 = 9. The same principle applies to √3 x √3, but with a crucial nuance.
Solving √3 x √3: A Step-by-Step Approach
The solution to √3 x √3 is remarkably simple once the underlying principles are understood. The core principle we need to employ is the property of radicals that states: √a x √a = a, where 'a' is a non-negative real number. Applying this to our problem:
√3 x √3 = 3
This is because the square root of a number multiplied by itself cancels out the square root operation. Think of it as the inverse operation: the square root "undoes" the squaring operation.
The Power of Exponents: An Alternate Perspective
We can also approach this problem using the concept of exponents. Remember that a square root is equivalent to raising a number to the power of 1/2. Therefore, √3 can be written as 3^(1/2). Now, let's rewrite our equation using exponents:
3^(1/2) x 3^(1/2)
Recall the rule of exponents: a^m x a^n = a^(m+n). Applying this rule:
3^(1/2 + 1/2) = 3^1 = 3
This demonstrates that using exponents leads to the same result: √3 x √3 = 3. This approach reinforces the mathematical consistency between radicals and exponents.
Beyond the Basics: Expanding Our Understanding
While the solution to √3 x √3 is simple, the underlying principles have far-reaching consequences in more advanced mathematical contexts. Let's explore some of these:
-
Simplifying Radical Expressions: Understanding the properties of radicals is crucial for simplifying complex radical expressions. For example, simplifying √75 involves factoring 75 into its prime factors (3 x 5 x 5) and then simplifying the expression as 5√3. This ability to manipulate radicals is essential in algebra and calculus.
-
Solving Quadratic Equations: Quadratic equations, which are equations of the form ax² + bx + c = 0, often involve square roots in their solutions. The quadratic formula, a cornerstone of algebra, uses square roots to find the values of 'x' that satisfy the equation. Understanding how to work with radicals is crucial for successfully solving these types of equations.
-
Trigonometry and Geometry: Trigonometric functions, like sine, cosine, and tangent, often involve radical expressions. Many geometric calculations, especially those involving triangles, utilize radical expressions to represent lengths and angles. For instance, finding the diagonal of a square with side length 'a' involves calculating √(a² + a²) = a√2.
-
Calculus: The concept of limits and derivatives in calculus often necessitates simplifying and manipulating radical expressions to evaluate limits and find derivatives of functions involving square roots. The ability to work smoothly with radicals is therefore important for advanced calculus.
-
Complex Numbers: While beyond the scope of this article, the square root of a negative number leads into the realm of imaginary numbers (like √-1 = i) and complex numbers (which combine real and imaginary numbers). The foundations laid here in understanding real square roots extend to this broader mathematical landscape.
Frequently Asked Questions (FAQ)
Q: Is √3 x √3 the same as (√3)²?
A: Yes, absolutely. Squaring a number is the same as multiplying it by itself. Therefore, (√3)² = √3 x √3 = 3.
Q: Can I use a calculator to solve √3 x √3?
A: Yes, a calculator can be used to find the individual value of √3 (approximately 1.732) and then multiply that by itself. However, understanding the underlying mathematical principles is far more valuable than simply obtaining a numerical answer.
Q: What if the numbers inside the square roots were different? For example, √3 x √2?
A: In this case, you cannot simply multiply the numbers inside the square roots. The rule √a x √a = a only applies when the radicands are the same. √3 x √2 simplifies to √6.
Q: What about higher-order roots? Does the same principle apply to cube roots or fourth roots?
A: The principle extends to higher-order roots. For example, ³√5 x ³√5 x ³√5 = 5, and ⁴√7 x ⁴√7 x ⁴√7 x ⁴√7 = 7. The key is that you need as many factors as the index of the root to eliminate the radical.
Conclusion: Mastering the Fundamentals
While √3 x √3 appears simple on the surface, it acts as a gateway to deeper understanding of essential mathematical concepts like radicals, exponents, and their applications in various fields. By mastering these fundamental principles, you pave the way for tackling more complex mathematical problems with confidence and ease. The ability to manipulate and simplify radical expressions is not just a mathematical skill; it's a crucial tool for success in higher-level mathematics and beyond. Remember, the true value lies not just in the answer (3), but in the journey of understanding the why and how. Continue to explore and expand your mathematical knowledge, and you will unlock a world of fascinating possibilities.
Latest Posts
Latest Posts
-
Names Of Endearment In Spanish
Sep 11, 2025
-
Compound Int Formula In Excel
Sep 11, 2025
-
Life Cycle Of The Ladybird
Sep 11, 2025
-
2 To The 3 Power
Sep 11, 2025
-
Meaning Of The Name Scarlet
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Root 3 Times Root 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.