Negative 3 Minus Negative 5
scising
Sep 16, 2025 · 5 min read
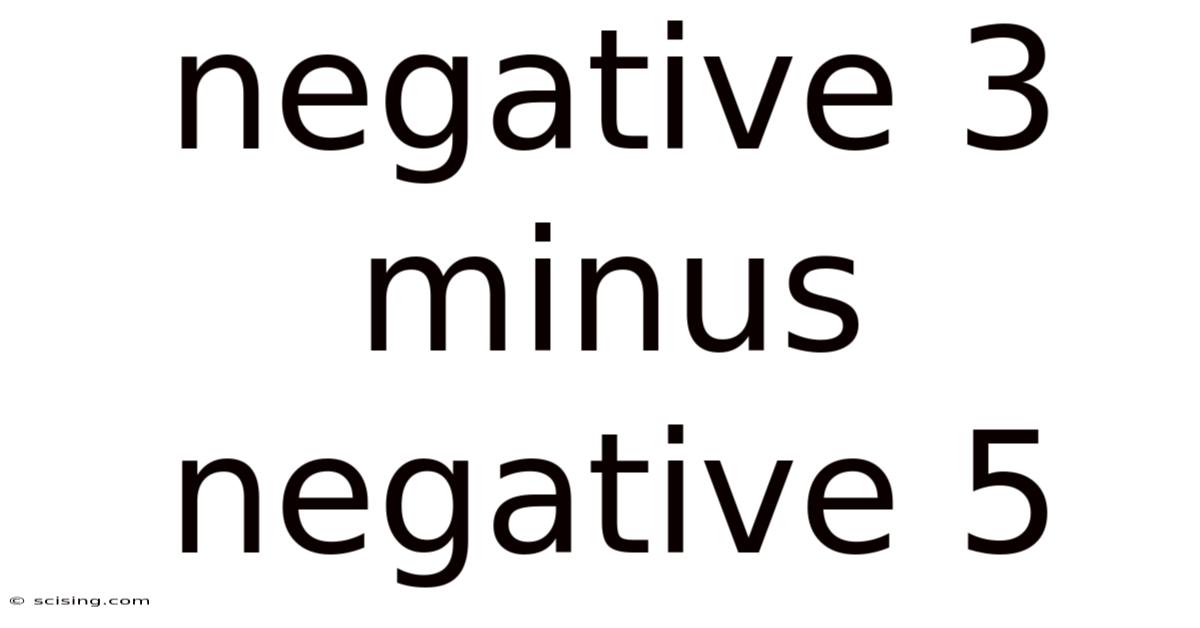
Table of Contents
Unraveling the Mystery: Negative 3 Minus Negative 5
Understanding negative numbers can be tricky, especially when subtraction enters the equation. Many find themselves stumbling over problems like "-3 - (-5)". This article will delve deep into this seemingly simple problem, explaining not just the answer but the underlying mathematical principles, offering different approaches to solving it, and addressing common misconceptions. By the end, you'll not only know the solution to -3 - (-5) but also possess a solid grasp of subtracting negative numbers.
Introduction: Navigating the World of Negative Numbers
Negative numbers represent values less than zero. They're crucial in various fields, from accounting (representing debt) to physics (representing temperature below zero). Mastering operations with negative numbers, including subtraction, is essential for anyone pursuing STEM fields or simply wanting a deeper understanding of mathematics. This article focuses specifically on the expression "-3 - (-5)", breaking down the process step-by-step and explaining the logic behind each step. We will explore multiple methods to solve this problem, ensuring a comprehensive understanding for learners of all levels.
Understanding Subtraction as Adding the Opposite
The key to understanding subtraction involving negative numbers lies in recognizing that subtracting a number is the same as adding its opposite. The opposite of a number is its additive inverse; it's the number that, when added to the original number, results in zero. For example:
- The opposite of 5 is -5 (because 5 + (-5) = 0)
- The opposite of -5 is 5 (because -5 + 5 = 0)
Therefore, the expression "-3 - (-5)" can be rewritten as "-3 + 5". This seemingly small change significantly simplifies the problem.
Method 1: The Number Line Approach
A number line is a visual representation of numbers. It's a fantastic tool for visualizing addition and subtraction. To solve -3 - (-5) using a number line:
-
Start at -3: Place your finger or a marker on -3 on the number line.
-
Subtracting a negative is like adding a positive: Since we're subtracting -5, we move to the right (the positive direction) on the number line.
-
Move 5 units to the right: Count five units to the right from -3.
-
The final position is the answer: You'll land on 2. Therefore, -3 - (-5) = 2.
Method 2: The Additive Inverse Method
This method directly applies the concept of the additive inverse. We've already established that subtracting a number is the same as adding its opposite.
-
Rewrite the expression: "-3 - (-5)" becomes "-3 + 5".
-
Add the numbers: Now, we simply add -3 and 5. Remember that adding a positive number to a negative number means finding the difference between their absolute values and keeping the sign of the larger number.
-
Calculate the difference: The absolute value of -3 is 3, and the absolute value of 5 is 5. The difference is 5 - 3 = 2.
-
Determine the sign: Since 5 (the positive number) has a larger absolute value, the result is positive.
-
Final Answer: Therefore, -3 + 5 = 2.
Method 3: Using Parentheses and the Order of Operations (PEMDAS/BODMAS)
While not strictly necessary for this simple problem, understanding the order of operations is crucial for more complex expressions involving negative numbers. PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) dictates the order in which operations should be performed.
-
Address Parentheses first: The parentheses in "-3 - (-5)" indicate that the negative sign applies to the 5.
-
Rewrite the expression: The expression remains "-3 - (-5)".
-
Subtraction as addition of the opposite: Rewrite the subtraction as addition of the opposite: -3 + 5.
-
Perform Addition: Add -3 and 5 to get 2.
-
Final Answer: Therefore, -3 - (-5) = 2.
Illustrative Examples: Expanding the Concept
Let's explore a few more examples to solidify your understanding:
-
-7 - (-2): This can be rewritten as -7 + 2 = -5. On a number line, you'd start at -7 and move 2 units to the right.
-
-10 - (-10): This simplifies to -10 + 10 = 0. Subtracting a number from itself always results in zero.
-
5 - (-3): This becomes 5 + 3 = 8. Subtracting a negative number results in a larger positive number.
Common Misconceptions and How to Avoid Them
Many students struggle with subtracting negative numbers due to these common misconceptions:
-
Ignoring the double negative: Failing to recognize that subtracting a negative is equivalent to adding a positive leads to incorrect answers.
-
Incorrect sign manipulation: Mistakes in changing the signs during the process of converting subtraction to addition are frequent.
-
Confusion with multiplication: Students might accidentally multiply the numbers instead of adding or subtracting them.
Frequently Asked Questions (FAQ)
Q: Why is subtracting a negative number the same as adding a positive number?
A: It's a consequence of the definition of subtraction and the properties of additive inverses. Subtraction is defined as adding the opposite. The opposite (or additive inverse) of a negative number is a positive number.
Q: Can I use a calculator to solve problems like this?
A: Yes, most calculators will correctly handle negative numbers and their subtraction. However, it's crucial to understand the underlying mathematical principles to avoid relying solely on a calculator and to troubleshoot potential errors.
Q: Are there other methods to solve problems involving negative numbers and subtraction?
A: Yes, other methods exist, including using algebraic manipulation and visualizing the problem using different graphical representations. The methods presented above provide a comprehensive foundation.
Q: What if I have a more complex expression with multiple subtractions of negative numbers?
A: Apply the same principle of converting each subtraction of a negative number into the addition of a positive number. Then, follow the order of operations (PEMDAS/BODMAS) to perform the calculations.
Conclusion: Mastering Negative Number Subtraction
Understanding subtraction of negative numbers is a cornerstone of mathematical literacy. While the concept might initially seem challenging, by understanding the relationship between subtraction and addition of the opposite, using visual aids like number lines, and carefully applying the order of operations, you can confidently tackle any problem involving negative numbers. The seemingly simple expression "-3 - (-5)" serves as a gateway to a broader understanding of arithmetic operations and their applications across numerous fields. Remember to practice regularly and break down complex problems into simpler steps, and you'll master this important mathematical skill.
Latest Posts
Latest Posts
-
How Far Is 30 Yards
Sep 16, 2025
-
Is Peter Pan A Fairy
Sep 16, 2025
-
How Long Is 78 Months
Sep 16, 2025
-
Chemical Equation For Baking Soda
Sep 16, 2025
-
Whats 20 Percent Of 500
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Negative 3 Minus Negative 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.