Whats 20 Percent Of 500
scising
Sep 16, 2025 · 5 min read
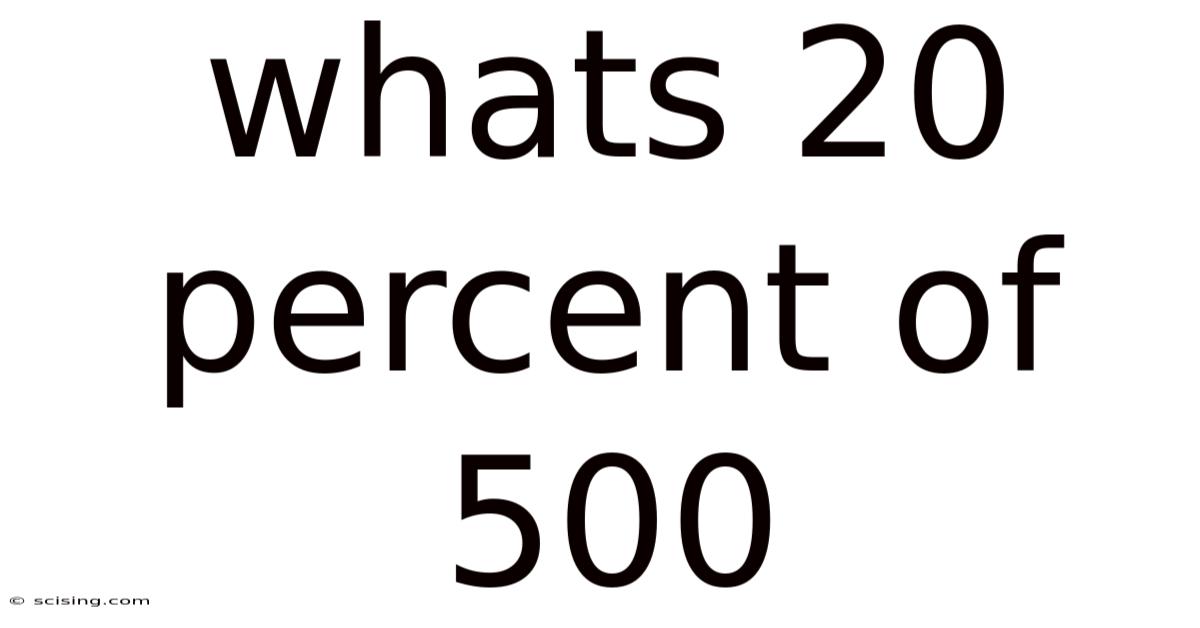
Table of Contents
What's 20 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 500 might seem like a simple task, easily solved with a quick calculation. But this seemingly straightforward question opens the door to a broader understanding of percentages, their significance in everyday life, and the various methods used to calculate them. This article will not only answer the question directly but also explore the underlying mathematical principles, practical applications, and common misconceptions surrounding percentages. We'll even delve into more advanced percentage calculations to solidify your understanding.
Introduction: Understanding Percentages
Percentages are a fundamental concept in mathematics expressing a proportion or fraction as a number out of 100. The symbol "%" denotes a percentage. Essentially, a percentage shows the relationship between a part and a whole. For example, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This means that for every 5 units, 1 unit represents 20%.
Understanding percentages is crucial in various real-life situations, from calculating discounts and sales tax to understanding financial reports, statistics, and even evaluating academic performance. Mastering percentage calculations equips you with a powerful tool for navigating the numerical world around us.
Calculating 20% of 500: The Basic Method
The most straightforward method to calculate 20% of 500 involves converting the percentage to a decimal and then multiplying it by the whole number.
-
Step 1: Convert the percentage to a decimal: To do this, divide the percentage by 100. So, 20% becomes 20/100 = 0.20.
-
Step 2: Multiply the decimal by the whole number: Multiply 0.20 by 500: 0.20 x 500 = 100.
Therefore, 20% of 500 is 100.
Alternative Methods: Exploring Different Approaches
While the above method is the most common, there are alternative ways to calculate percentages, each offering its own advantages depending on the context and your comfort level with mathematical operations.
-
Using Fractions: As mentioned earlier, 20% is equivalent to the fraction 1/5. Therefore, we can calculate 20% of 500 by dividing 500 by 5: 500 / 5 = 100. This method is particularly useful when dealing with percentages that easily convert to simple fractions (e.g., 50%, 25%, 10%).
-
Using Proportions: We can set up a proportion to solve this problem. Let 'x' represent 20% of 500. The proportion would be:
20/100 = x/500
Cross-multiplying gives us:
100x = 10000
Dividing both sides by 100 yields:
x = 100
-
Mental Math Techniques: For simple percentages like 20%, mental math can be surprisingly efficient. You can break down the calculation. 10% of 500 is 50 (500/10). Since 20% is double 10%, 20% of 500 is 2 * 50 = 100.
Beyond the Basics: More Complex Percentage Calculations
Let's expand our understanding by tackling more complex percentage problems. These examples will build on the foundational knowledge we've already established.
-
Finding the Percentage Increase or Decrease: Suppose a product initially costing 500 increases by 20%. To find the new price, we first calculate the increase: 20% of 500 = 100. Then, we add this increase to the original price: 500 + 100 = 600. The new price is 600. Conversely, if the price decreased by 20%, we would subtract the decrease (100) from the original price.
-
Finding the Original Value: Imagine a sale where an item is marked down 20% to 400. To find the original price, we need to work backward. If 400 represents 80% (100% - 20%) of the original price, we can set up a proportion:
80/100 = 400/x
Cross-multiplying and solving for 'x' gives us:
80x = 40000
x = 500
The original price was 500.
- Calculating Percentage Change: Let's say a quantity increases from 400 to 500. To calculate the percentage increase, we first find the difference: 500 - 400 = 100. Then, we divide the difference by the original value and multiply by 100: (100/400) * 100 = 25%. The quantity increased by 25%.
Practical Applications of Percentages in Everyday Life
Percentages are ubiquitous in our daily lives. Understanding them is essential for making informed decisions. Here are just a few examples:
-
Shopping: Calculating discounts, sales tax, and comparing prices. A 20% discount on a 500 item would save you 100, making the final price 400.
-
Finance: Understanding interest rates, loan repayments, and investment returns. A 20% annual interest rate on a 500 investment would yield 100 in interest after one year (assuming simple interest).
-
Statistics and Data Analysis: Interpreting survey results, understanding population demographics, and analyzing trends. If 20% of a survey population responded positively, it reveals valuable information about a particular characteristic.
-
Academic Performance: Calculating grades, evaluating progress, and comparing performance across different subjects. A score of 100 out of 500 might represent 20%, indicating areas for improvement.
Common Misconceptions About Percentages
Despite their apparent simplicity, percentages can sometimes be misinterpreted. Here are a few common misconceptions:
-
Adding Percentages Directly: You cannot simply add percentages together without considering the base value. A 10% increase followed by a 10% decrease does not result in the original value.
-
Confusing Percentage Points with Percentages: A change from 20% to 30% is a 10 percentage point increase, not a 50% increase.
-
Incorrect Base Value: When calculating percentage change, always use the original value as the base.
Frequently Asked Questions (FAQ)
Q: How do I calculate x% of y?
A: Convert x% to a decimal by dividing by 100 (x/100). Then, multiply the decimal by y.
Q: What is the easiest way to calculate percentages mentally?
A: Practice breaking down percentages into simpler fractions and multiples of 10%.
Q: Are there any online calculators for percentages?
A: Yes, numerous websites and apps provide percentage calculators for various calculations.
Q: How can I improve my understanding of percentages?
A: Practice solving various percentage problems, starting with simpler ones and gradually increasing the complexity.
Conclusion: Mastering the Art of Percentages
Understanding percentages is a valuable life skill. From everyday shopping to complex financial analyses, the ability to calculate and interpret percentages accurately is crucial for informed decision-making. While finding 20% of 500 is a simple calculation, the underlying principles extend far beyond this specific example. By grasping these principles and practicing regularly, you can confidently navigate the world of percentages and use them to your advantage in countless situations. Remember to always double-check your work and understand the context of your calculations to avoid common misconceptions. The journey from a simple percentage calculation to a deeper understanding of its implications is a rewarding one, equipping you with essential tools for numerical literacy.
Latest Posts
Latest Posts
-
200 Mg To Ml Syringe
Sep 16, 2025
-
How Many Ounces In 500ml
Sep 16, 2025
-
Seasons Of The Year Spanish
Sep 16, 2025
-
Capacitor And Resistor In Series
Sep 16, 2025
-
Blood Clot In Hand Pictures
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.