Lcm Of 4 And 12
scising
Sep 12, 2025 · 6 min read
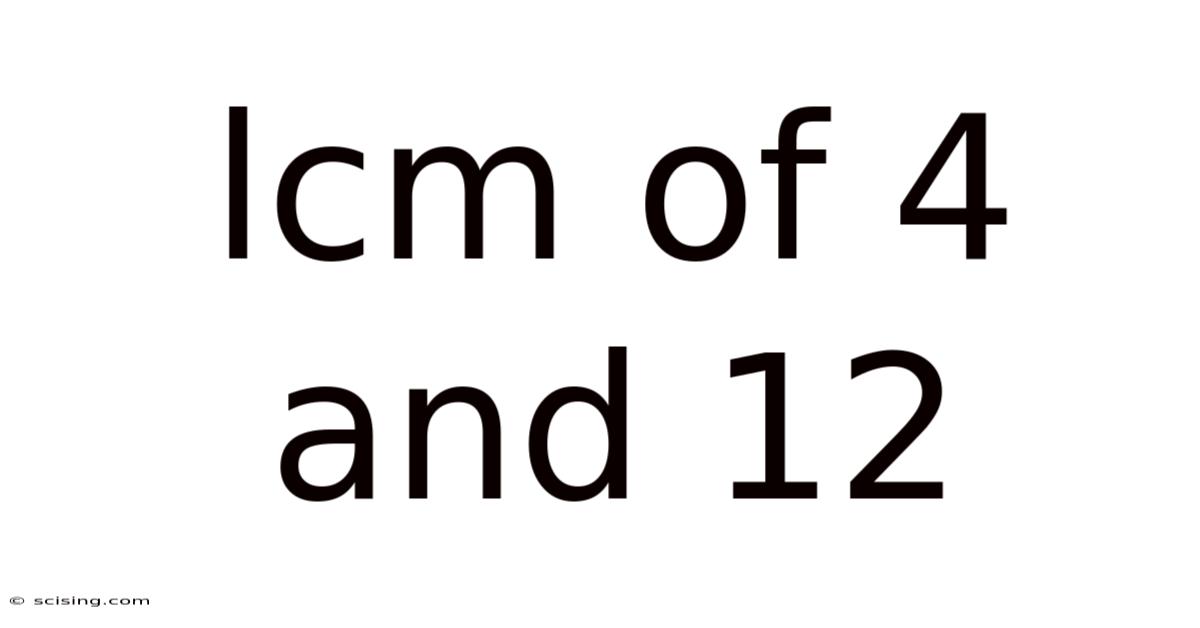
Table of Contents
Understanding the LCM of 4 and 12: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, ratios, and solving real-world problems involving cycles or repetitions. This article will thoroughly explore the LCM of 4 and 12, providing a detailed explanation suitable for learners of all levels. We will cover multiple methods for calculating the LCM, delve into the underlying mathematical principles, and explore practical applications to solidify your understanding. This comprehensive guide will not only teach you how to find the LCM of 4 and 12 but also equip you with the knowledge to tackle more complex LCM problems.
What is a Least Common Multiple (LCM)?
Before we dive into the specifics of finding the LCM of 4 and 12, let's define the term. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Methods for Finding the LCM of 4 and 12
Several methods can be used to determine the LCM of 4 and 12. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 12: 12, 24, 36, 48...
The smallest number appearing in both lists is 12. Therefore, the LCM of 4 and 12 is 12.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. The prime factors are the prime numbers that, when multiplied together, give the original number.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM using prime factorization:
- Identify all the prime factors present in either factorization. In this case, we have 2 and 3.
- For each prime factor, take the highest power that appears in any of the factorizations. The highest power of 2 is 2², and the highest power of 3 is 3¹.
- Multiply these highest powers together: 2² x 3 = 4 x 3 = 12.
Therefore, the LCM of 4 and 12, using prime factorization, is 12.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers.
-
Find the GCD of 4 and 12: The GCD is the largest number that divides both 4 and 12 without leaving a remainder. The divisors of 4 are 1, 2, and 4. The divisors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common divisor is 4.
-
Use the formula: LCM(a, b) = (a x b) / GCD(a, b)
LCM(4, 12) = (4 x 12) / 4 = 12
This method highlights the interconnectedness between LCM and GCD, offering an alternative approach to finding the LCM.
Understanding the Result: Why is the LCM of 4 and 12 equal to 12?
The LCM of 4 and 12 being 12 makes intuitive sense. 12 is a multiple of both 4 (4 x 3 = 12) and 12 (12 x 1 = 12). Furthermore, there is no smaller positive integer that satisfies this condition. This illustrates the core concept of the LCM: the smallest number divisible by all given numbers.
Real-World Applications of LCM
Understanding LCM isn't just about abstract mathematical concepts; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses leaving a depot at different intervals. One bus leaves every 4 hours, and another leaves every 12 hours. The LCM (12 hours) determines when both buses will leave the depot at the same time again.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator, simplifying the calculation process.
-
Cyclic Events: Consider events that repeat cyclically, such as the phases of the moon or the timing of tides. LCM can help predict when these events will coincide.
-
Construction and Design: In construction or design projects involving repetitive patterns or measurements, LCM helps ensure consistent and harmonious arrangements.
Beyond 4 and 12: Extending the Concepts
The methods described above can be applied to find the LCM of any two or more integers. For larger numbers, the prime factorization method is generally more efficient. For three or more numbers, the process remains similar; find the prime factorization of each number, identify the highest power of each prime factor, and multiply them together.
For example, let's find the LCM of 6, 8, and 12:
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The highest power of 2 is 2³, and the highest power of 3 is 3¹. Therefore, LCM(6, 8, 12) = 2³ x 3 = 8 x 3 = 24.
Frequently Asked Questions (FAQ)
-
Q: What if the two numbers have no common factors other than 1?
A: If the two numbers are relatively prime (meaning their GCD is 1), then their LCM is simply their product. For example, the LCM of 5 and 7 is 35 (5 x 7 = 35).
-
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, as seen in the example of 4 and 12. If one number is a multiple of the other, the larger number is the LCM.
-
Q: Is there a formula to directly calculate the LCM without using the GCD?
A: While there isn't a single, direct formula independent of GCD, the prime factorization method effectively achieves this by directly working with the prime factors.
-
Q: How can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM. Consult your calculator's manual for instructions.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with diverse applications. This article has provided a comprehensive guide to understanding and calculating the LCM of 4 and 12, using various methods and exploring the underlying mathematical principles. We've also highlighted the practical significance of LCM in various real-world scenarios. Mastering the concepts of LCM opens doors to a deeper understanding of number theory and its practical uses in various fields. Remember to practice using different methods to solidify your understanding and tackle more complex problems with confidence. The journey to mastering LCM is a rewarding one, leading to improved problem-solving skills and a more profound appreciation of mathematical concepts.
Latest Posts
Latest Posts
-
Hno3 Is A Strong Acid
Sep 12, 2025
-
Pseudostratified Ciliated Columnar Epithelial Tissue
Sep 12, 2025
-
30 40 As A Percentage
Sep 12, 2025
-
Devil And White City Book
Sep 12, 2025
-
Is Usted Formal Or Informal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.