30 40 As A Percentage
scising
Sep 12, 2025 · 5 min read
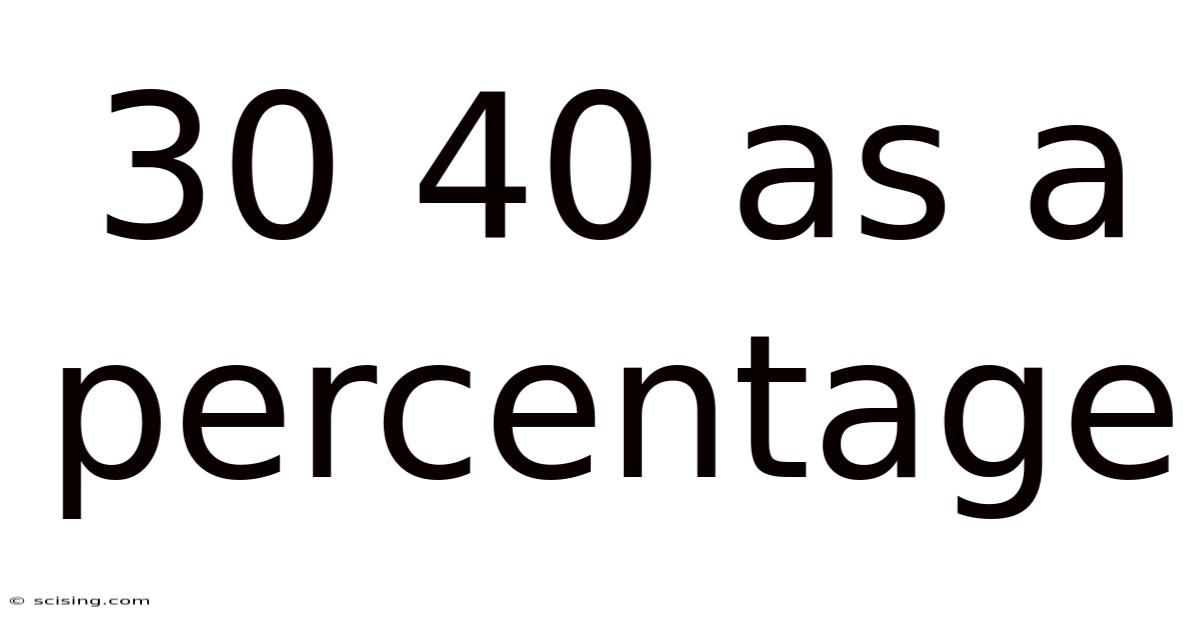
Table of Contents
Decoding the Percentage: Understanding 30 out of 40 as a Percentage
Many aspects of daily life involve calculating percentages. From understanding exam scores and sales discounts to comprehending financial reports and statistical data, percentage calculations are essential. This comprehensive guide will delve deep into understanding how to calculate 30 out of 40 as a percentage, exploring the process, its applications, and providing a deeper understanding of percentage calculations in general. This article will equip you with the knowledge and skills to confidently tackle similar percentage problems.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol % is used to represent percentage. Essentially, it represents a portion of a whole. For instance, 50% means 50 out of 100, or one-half. Understanding this fundamental concept is crucial for any percentage calculation.
Calculating 30 out of 40 as a Percentage: The Step-by-Step Guide
Let's break down the calculation of 30 out of 40 as a percentage into simple, manageable steps:
Step 1: Set up the Fraction
First, express the given numbers as a fraction. In this case, 30 is the part and 40 is the whole. This is represented as:
30/40
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
30 ÷ 40 = 0.75
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.75 x 100 = 75%
Therefore, 30 out of 40 is equal to 75%.
Alternative Calculation Method: Using Proportions
Another way to approach this problem is by using proportions. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the percentage:
x/100 = 30/40
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
40x = 3000
Then, divide both sides by 40:
x = 3000/40 = 75
Therefore, x = 75%, confirming our previous calculation.
Real-World Applications of Percentage Calculations: Examples
Understanding percentage calculations has widespread applications in various aspects of life. Here are a few examples:
-
Academic Performance: Imagine a student scores 30 out of 40 marks in a test. Calculating the percentage (75%) provides a clear understanding of their performance relative to the total marks. This allows for easy comparison with other students and tracking of progress over time.
-
Sales and Discounts: Stores often advertise discounts as percentages. For example, a 25% discount on an item means you pay 75% of the original price. Understanding percentage calculations is essential for determining the final price after a discount.
-
Financial Literacy: Percentage calculations are fundamental to understanding interest rates on loans, savings accounts, and investments. They allow for the calculation of interest earned or paid over time.
-
Data Analysis and Statistics: Percentages are frequently used to represent data in graphs, charts, and reports. They provide a concise way to illustrate proportions and trends.
-
Scientific Research: In scientific research, percentages are used to express the frequency of occurrences, the success rate of experiments, and to present data concisely in research papers and presentations.
Beyond the Basics: More Complex Percentage Problems
While 30 out of 40 is a relatively straightforward calculation, percentage problems can become more complex. Let's explore some variations:
-
Calculating the Percentage Increase or Decrease: Suppose a quantity increases from 40 to 50. To calculate the percentage increase, first find the difference (50 - 40 = 10), then divide the difference by the original value (10/40 = 0.25) and multiply by 100 (0.25 * 100 = 25%). Therefore, there's a 25% increase. Percentage decrease is calculated similarly.
-
Finding the Original Value: If an item is discounted by 20% and now costs $80, to find the original price, you need to work backward. Since the current price represents 80% of the original price, you can set up the equation: 0.8x = 80, where 'x' is the original price. Solving for x gives you x = $100.
-
Calculating Percentages of Percentages: Sometimes, you need to calculate percentages of percentages. For example, finding 10% of 25% of a number involves multiplying the percentages as decimals and then multiplying by the original number.
Frequently Asked Questions (FAQ)
Q: What if I have a different number of items, say 25 out of 50? How would I calculate the percentage?
A: The process remains the same. You would set up the fraction 25/50, convert it to a decimal (25 ÷ 50 = 0.5), and then multiply by 100 to get the percentage (0.5 x 100 = 50%).
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators are very helpful, especially for more complex percentage calculations. Most calculators have a percentage function (%) which simplifies the process.
Q: What if the numbers are not whole numbers, but decimals?
A: The process is still the same. You would follow the same steps, converting the fraction to a decimal, then multiplying by 100 to obtain the percentage.
Q: Are there any online tools to help with percentage calculations?
A: Yes, many websites and online calculators are available that can perform percentage calculations quickly and accurately.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a valuable skill applicable to numerous aspects of life. This guide detailed the process of calculating 30 out of 40 as a percentage (75%), using both fractional and proportional methods. We also explored the broader applications of percentage calculations and addressed common questions. By mastering these concepts, you are better equipped to confidently navigate percentage-related problems in your academic, professional, and personal life. Remember to practice regularly to reinforce your understanding and build your confidence in tackling increasingly complex percentage calculations.
Latest Posts
Latest Posts
-
How To Determine Square Yards
Sep 12, 2025
-
Food Chain Of The Taiga
Sep 12, 2025
-
Car Gar Zar Verbs Spanish
Sep 12, 2025
-
Is Sugar Polar Or Nonpolar
Sep 12, 2025
-
Does A Duck Have Ears
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 30 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.