D 2y Dx 2 Formula
scising
Sep 14, 2025 · 5 min read
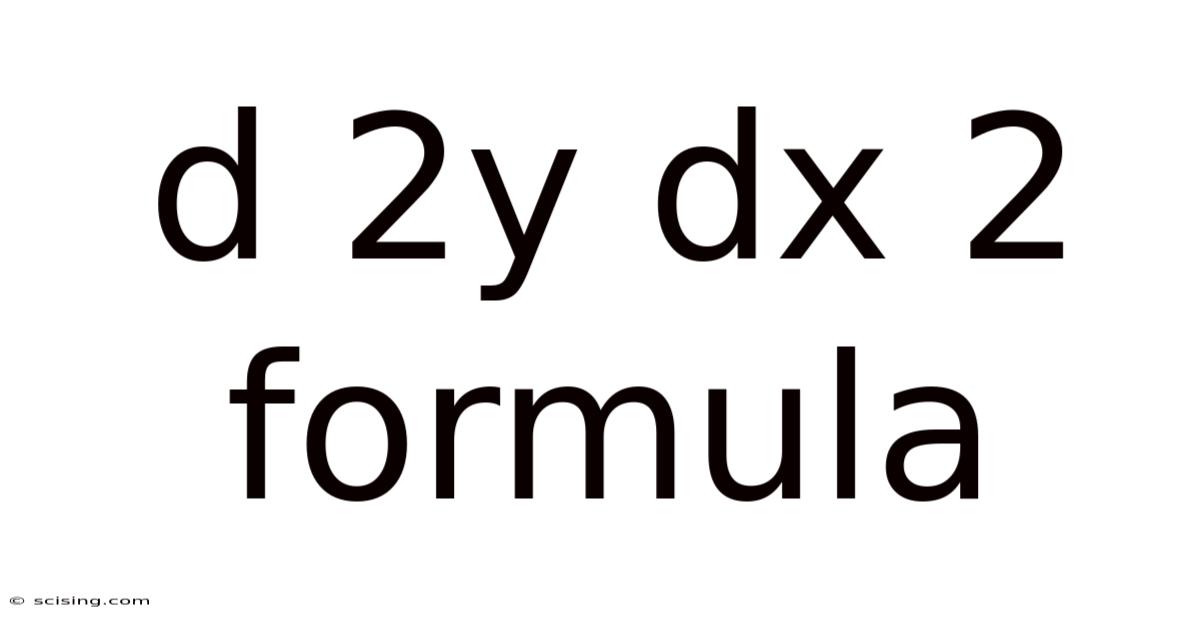
Table of Contents
Del Squared (∇²) and its Applications: A Deep Dive into the ∂²y/∂x² Formula
The formula ∂²y/∂x², often written as ∇²y or Δy, represents the second-order partial derivative of a function y with respect to x. This seemingly simple expression plays a crucial role in numerous fields, including physics, engineering, and computer science. Understanding its meaning, derivation, and applications is essential for anyone working with differential equations and multivariable calculus. This article provides a comprehensive exploration of ∂²y/∂x², delving into its calculation, physical interpretations, and practical uses.
Understanding Partial Derivatives
Before diving into the second-order partial derivative, let's revisit the concept of a partial derivative. Consider a function of multiple variables, y = f(x, z, t). A partial derivative measures the rate of change of the function with respect to one variable, while holding all other variables constant.
For instance, ∂y/∂x represents the partial derivative of y with respect to x. This means we treat z and t as constants and differentiate y with respect to x using standard differentiation rules. Similarly, ∂y/∂z and ∂y/∂t represent the partial derivatives with respect to z and t, respectively.
Deriving the Second-Order Partial Derivative (∂²y/∂x²)
The second-order partial derivative, ∂²y/∂x², is simply the partial derivative of the first partial derivative. In other words, we first find ∂y/∂x and then differentiate the result again with respect to x, keeping other variables constant.
Let's illustrate this with an example. Suppose we have the function:
y = x³ + 2xz + z²
- First-order partial derivative (∂y/∂x):
Differentiating with respect to x, treating z as a constant, we get:
∂y/∂x = 3x² + 2z
- Second-order partial derivative (∂²y/∂x²):
Now, we differentiate ∂y/∂x with respect to x:
∂²y/∂x² = ∂/∂x (3x² + 2z) = 6x
Thus, the second-order partial derivative of y with respect to x is 6x.
The Laplacian Operator (∇²)
The expression ∂²y/∂x² is often encountered within the context of the Laplacian operator, denoted as ∇² (del squared) or Δ (Delta). The Laplacian is a differential operator that gives the divergence of the gradient of a function. In Cartesian coordinates (x, y, z), the Laplacian of a scalar function y is defined as:
∇²y = ∂²y/∂x² + ∂²y/∂y² + ∂²y/∂z²
This means it sums the second-order partial derivatives with respect to each spatial dimension. The Laplacian is a crucial operator in numerous physical phenomena.
Physical Interpretations and Applications
The second-order partial derivative ∂²y/∂x² holds significant physical interpretations depending on the context:
-
Curvature: In the context of a curve described by the function y(x), ∂²y/∂x² represents the curvature of the curve at a given point. A positive value indicates concavity upwards, while a negative value indicates concavity downwards. Zero indicates an inflection point.
-
Acceleration: If y represents displacement and x represents time, then ∂²y/∂x² represents acceleration. This is a fundamental concept in classical mechanics.
-
Heat Diffusion: In the heat equation, ∂²y/∂x² describes the rate of change of the temperature gradient. This governs how heat spreads through a material over time.
-
Wave Propagation: In the wave equation, ∂²y/∂x² describes the spatial variation of displacement. This helps model how waves travel through space.
-
Electrostatics and Gravitation: In electrostatics and gravitation, the Laplacian of the potential function is proportional to the charge or mass density respectively. This is described by Poisson's equation: ∇²V = -ρ/ε₀ (electrostatics) or ∇²Φ = -4πGρ (gravitation), where V is the electric potential, Φ is the gravitational potential, ρ is the charge/mass density, ε₀ is the permittivity of free space, and G is the gravitational constant.
-
Image Processing: In image processing, the Laplacian is used for edge detection. The second-order derivatives highlight abrupt changes in pixel intensity, which correspond to edges.
-
Fluid Dynamics: The Laplacian appears in the Navier-Stokes equations, which describe the motion of viscous fluids. It's related to the diffusion of momentum.
-
Quantum Mechanics: The Laplacian appears in the Schrödinger equation, a fundamental equation in quantum mechanics. It represents the kinetic energy operator.
Solving Differential Equations Involving ∂²y/∂x²
Many differential equations in physics and engineering involve the second-order partial derivative. These equations often require sophisticated mathematical techniques to solve, including:
-
Separation of variables: This method reduces the partial differential equation to a set of ordinary differential equations.
-
Fourier series and transforms: These techniques are powerful tools for solving linear partial differential equations.
-
Green's functions: These functions provide a systematic approach to solving inhomogeneous differential equations.
-
Numerical methods: For complex equations that lack analytical solutions, numerical methods such as finite difference or finite element methods are employed.
Frequently Asked Questions (FAQ)
Q1: What is the difference between ∂²y/∂x² and d²y/dx²?
A: ∂²y/∂x² denotes a partial derivative, meaning it's used when y is a function of multiple variables. d²y/dx² denotes an ordinary derivative, used when y is a function of a single variable.
Q2: Can ∂²y/∂x² be negative?
A: Yes, ∂²y/∂x² can be negative. A negative value indicates concavity downwards (in the context of curves) or certain aspects of acceleration/deceleration.
Q3: How do I calculate ∂²y/∂x² for more complex functions?
A: For more complex functions, apply the standard rules of differentiation (product rule, chain rule, etc.) sequentially. Remember to treat all variables except x as constants when differentiating with respect to x.
Q4: What are some software tools that can calculate ∂²y/∂x²?
A: Many mathematical software packages, including Mathematica, Maple, and MATLAB, can perform symbolic and numerical calculations of partial derivatives.
Q5: What are some real-world applications where understanding ∂²y/∂x² is crucial?
A: Understanding ∂²y/∂x² is crucial in various fields, including designing bridges (structural mechanics), modeling weather patterns (fluid dynamics), developing medical imaging techniques (image processing), and creating video games (physics engines).
Conclusion
The second-order partial derivative ∂²y/∂x², a seemingly simple mathematical concept, has profound implications across diverse scientific and engineering disciplines. Its significance stems from its ability to describe curvature, acceleration, diffusion, and wave propagation – fundamental processes governing numerous physical phenomena. Mastering its calculation and interpretation is essential for anyone pursuing a deeper understanding of differential equations and their applications in the real world. From understanding the bending of beams to predicting the spread of heat, ∂²y/∂x² provides the mathematical framework for interpreting and modeling crucial aspects of our universe. Its continued study remains vital for technological advancement and scientific exploration.
Latest Posts
Latest Posts
-
Ave Maria Celine Dion Lyrics
Sep 14, 2025
-
What Is 80 Of 5
Sep 14, 2025
-
How Much Is 34 Ounces
Sep 14, 2025
-
The Substrate For Pepsin Is
Sep 14, 2025
-
Use Confound In A Sentence
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about D 2y Dx 2 Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.