What Is 80 Of $5
scising
Sep 14, 2025 · 5 min read
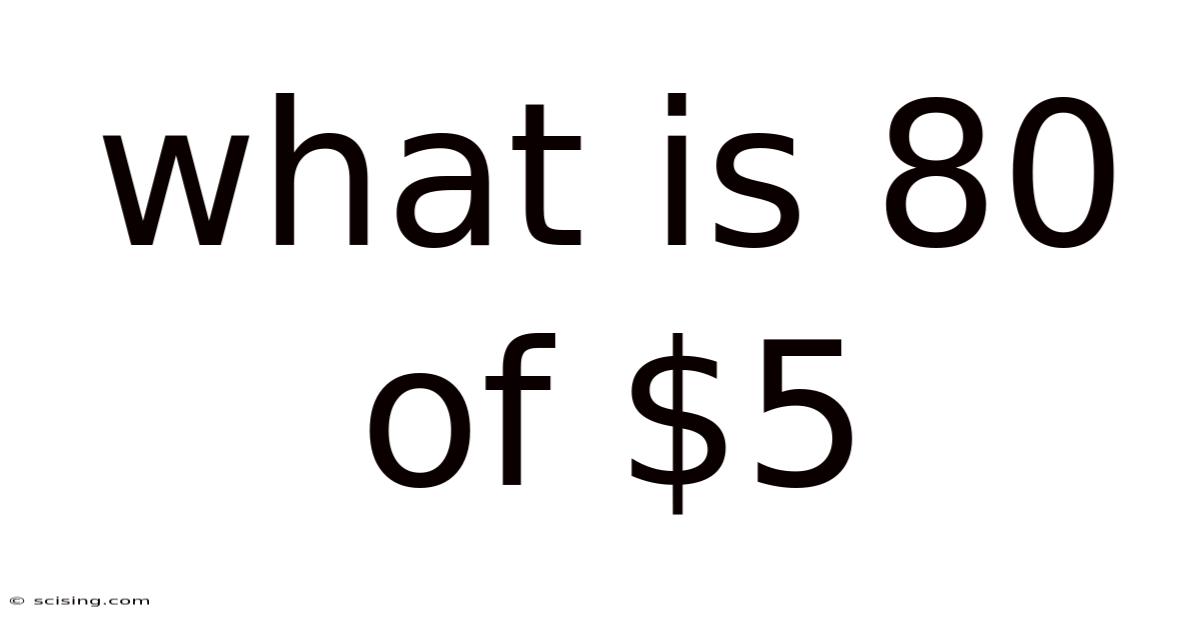
Table of Contents
What is 80% of $5? A Deep Dive into Percentages and Their Applications
Finding 80% of $5 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from budgeting and finance to sales and statistics. This article will not only answer the immediate question but also explore the broader concepts of percentages, providing you with a robust understanding and practical skills to tackle similar problems.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 80% means 80 out of 100, which can be written as the fraction 80/100 or the decimal 0.8. This understanding is crucial for calculating percentages of any amount.
Calculating 80% of $5: The Basic Approach
The most straightforward way to find 80% of $5 is to convert the percentage to a decimal and multiply it by the total amount.
-
Step 1: Convert the percentage to a decimal: 80% is equivalent to 0.8 (divide 80 by 100).
-
Step 2: Multiply the decimal by the amount: 0.8 * $5 = $4
Therefore, 80% of $5 is $\boxed{$4}$.
Alternative Methods: Exploring Different Approaches
While the method above is the most efficient for this specific problem, let's explore other methods to reinforce the understanding of percentages and provide flexibility for different scenarios.
-
Using Fractions: We can also express 80% as the fraction 80/100, which simplifies to 4/5. Multiplying $5 by 4/5 gives us (4/5) * $5 = $4. This method highlights the relationship between fractions and percentages.
-
Proportions: We can set up a proportion: 80/100 = x/$5. Cross-multiplying gives us 100x = 400, and solving for x gives us x = $4. This approach is useful when dealing with more complex percentage problems.
Beyond the Calculation: Real-World Applications of Percentages
The ability to calculate percentages is invaluable in numerous real-world situations:
-
Finance: Calculating interest on loans, savings accounts, or investments. Understanding interest rates and compound interest relies heavily on percentage calculations. For example, if you have a savings account with a 5% annual interest rate, calculating the interest earned each year requires percentage calculations.
-
Sales and Discounts: Determining the sale price of an item after a percentage discount. If a store offers a 20% discount on a $100 item, you'll need to calculate 20% of $100 and subtract it from the original price.
-
Taxes: Calculating sales tax or income tax. Taxes are often expressed as percentages of the purchase price or income.
-
Statistics and Data Analysis: Percentages are fundamental in representing and interpreting data. For instance, analyzing survey results often involves expressing responses as percentages of the total number of respondents. Understanding percentage change is also crucial in tracking trends and growth.
-
Tips and Gratuities: Calculating tips in restaurants or service charges. A common tip is 15% or 20% of the bill, requiring a percentage calculation.
-
Budgeting: Allocating a percentage of your income to different expenses, like housing, food, transportation, and entertainment. Effective budgeting involves carefully planning how much of your income will be allocated to each expense category.
Expanding the Knowledge: More Complex Percentage Problems
Let's move beyond the simple calculation of 80% of $5 and explore more complex scenarios to further solidify your understanding of percentages:
-
Finding the Original Amount: If an item is on sale for $20 after a 25% discount, what was the original price? This involves working backward from the discounted price to find the original amount. Let's say the original price is 'x'. Then, x - 0.25x = $20. Solving for x, we get 0.75x = $20, hence x = $20 / 0.75 = $26.67 (approximately).
-
Percentage Increase or Decrease: Calculating the percentage increase or decrease between two values. For example, if sales increased from $1000 to $1200, the percentage increase is ((1200-1000)/1000) * 100% = 20%.
-
Compounding Percentages: Calculating the effect of multiple percentage changes. For instance, if a price increases by 10% and then decreases by 10%, the final price is not the same as the original price due to the compounding effect. Understanding compounding is particularly important in finance and investment.
-
Percentage Points vs. Percentage Change: It's crucial to understand the difference between percentage points and percentage change. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage change.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage of a larger number? A: The same principles apply. Convert the percentage to a decimal and multiply it by the larger number.
-
Q: How do I calculate percentages quickly without a calculator? A: For simple percentages like 10%, 25%, or 50%, you can use mental math techniques. For example, 10% is simply moving the decimal point one place to the left. 50% is half the number. For other percentages, you can break them down into simpler fractions (e.g., 75% is 3/4).
-
Q: Are there any online tools or calculators for calculating percentages? A: Yes, numerous online calculators are available to help with percentage calculations, simplifying the process and providing quick results. However, it's important to understand the underlying principles and be able to perform calculations manually.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not just about solving simple mathematical problems; it's about developing a fundamental skill applicable to various aspects of life. From managing your finances to analyzing data, grasping the concept of percentages empowers you to make informed decisions and navigate the world more effectively. The simple calculation of 80% of $5 serves as a springboard to explore a vast and valuable mathematical concept with real-world implications. Practice applying these methods in different scenarios, and you'll find yourself becoming increasingly confident and proficient in handling percentages with ease. Remember, the key is not just memorizing formulas but understanding the underlying principles and developing the ability to approach different percentage problems strategically.
Latest Posts
Latest Posts
-
How Much Is 80 Ounces
Sep 15, 2025
-
Is Robanging Considered Erotic Roleplay
Sep 15, 2025
-
Function Examples In Real Life
Sep 15, 2025
-
1 1 16 In To Mm
Sep 15, 2025
-
What Is A Molecular Element
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of $5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.