5 20 As A Percent
scising
Sep 14, 2025 · 5 min read
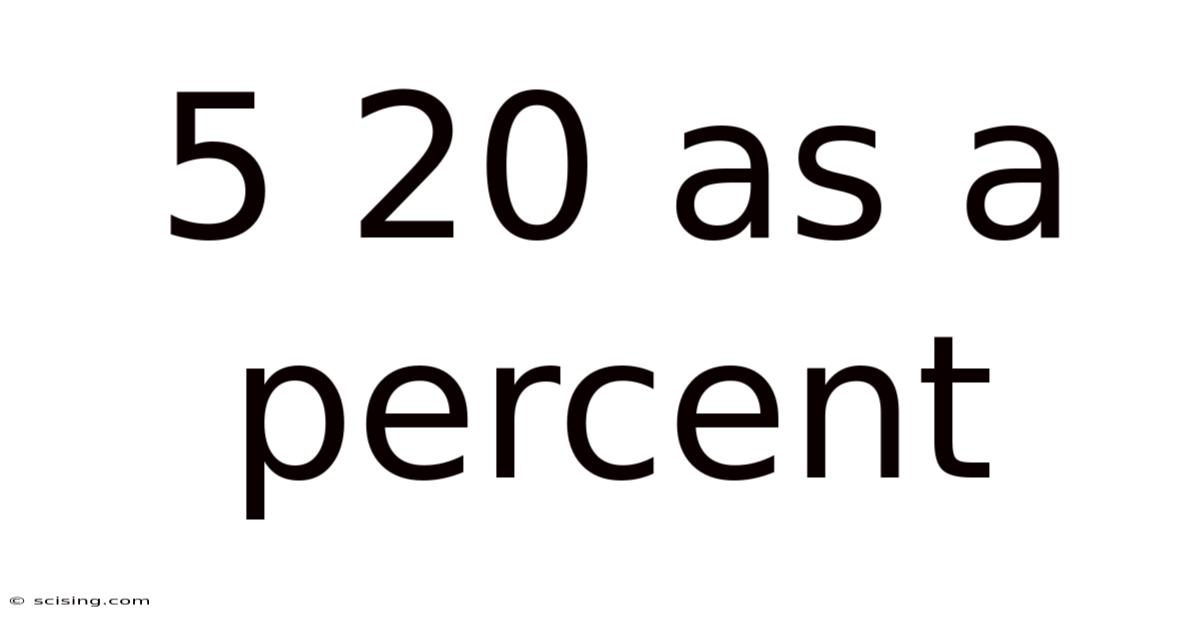
Table of Contents
Understanding 5/20 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will walk you through the process of converting the fraction 5/20 into a percentage, explaining the underlying concepts and providing practical examples. We'll delve into the steps involved, explore the underlying mathematical principles, and address frequently asked questions to ensure a thorough understanding of this important concept. By the end, you'll not only know the answer but also possess the tools to confidently tackle similar conversions.
Understanding Fractions and Percentages
Before diving into the specifics of 5/20, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, while the numerator indicates the number of parts being considered.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100.
The core relationship between fractions and percentages is that a percentage is simply a fraction with a denominator of 100. Converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100, then expressing the numerator as the percentage.
Method 1: Simplifying the Fraction and then Converting to a Percentage
The fraction 5/20 can be simplified before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 5 and 20 is 5.
-
Simplify the fraction: Divide both the numerator and the denominator by 5:
5 ÷ 5 = 1 20 ÷ 5 = 4
This simplifies the fraction 5/20 to 1/4.
-
Convert the simplified fraction to a percentage: To convert a fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by a number that will result in a denominator of 100. In this case, we multiply by 25:
1 × 25 = 25 4 × 25 = 100
This gives us the equivalent fraction 25/100.
-
Express as a percentage: Since a percentage is a fraction out of 100, 25/100 is equivalent to 25%.
Therefore, 5/20 is equal to 25%.
Method 2: Direct Conversion using Division
Another approach is to directly convert the fraction to a decimal and then to a percentage.
-
Divide the numerator by the denominator: Divide 5 by 20:
5 ÷ 20 = 0.25
-
Convert the decimal to a percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.25 × 100 = 25%
Therefore, using this method also confirms that 5/20 is equal to 25%.
The Mathematical Principle Behind the Conversion
The conversion from a fraction to a percentage fundamentally relies on the concept of proportionality. We're essentially finding an equivalent ratio where the denominator is 100. This is achieved through multiplication or division, ensuring that the ratio remains the same while the denominator is transformed. The multiplication factor is determined by dividing 100 by the original denominator. In the case of 5/20, this factor is 100/20 = 5. Multiplying both numerator and denominator by 5 yields 25/100, directly representing 25%.
This principle extends to all fraction-to-percentage conversions. The core idea is to maintain the proportional relationship between the parts and the whole while expressing that relationship in terms of a hundredth.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in many real-world situations. Here are a few examples:
- Discounts: A store offering a 25% discount on an item is essentially offering a discount equal to 1/4 of the original price.
- Grades: A student scoring 15 out of 20 on a test can calculate their percentage score (75%) by converting 15/20 to a percentage.
- Financial Statements: Financial reports often use percentages to express ratios and proportions of different financial figures.
- Probability: Probabilities are often expressed as percentages to indicate the likelihood of an event occurring.
- Data Analysis: Percentages are widely used to represent data proportions in various charts and graphs.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage. The process involves finding an equivalent fraction with a denominator of 100 or dividing the numerator by the denominator and then multiplying by 100.
Q2: What if the fraction results in a repeating decimal when converted to a percentage?
A2: If the decimal repeats, you can round the percentage to a suitable number of decimal places depending on the required level of precision.
Q3: Is there a quicker way to convert simple fractions to percentages?
A3: For common fractions, memorizing their percentage equivalents can speed up the process. For example, 1/2 = 50%, 1/4 = 25%, 1/5 = 20%, etc.
Q4: How do I convert a percentage back into a fraction?
A4: To convert a percentage back into a fraction, simply divide the percentage by 100 and simplify the resulting fraction. For instance, 75% becomes 75/100, which simplifies to 3/4.
Q5: Why is the percentage so important in everyday life?
A5: Percentages provide a standardized way to compare proportions and ratios across different contexts. They simplify complex numerical relationships making comparisons easier to understand and interpret.
Conclusion
Converting 5/20 to a percentage is a straightforward process that involves simplifying the fraction (if possible) and then expressing it as a fraction with a denominator of 100. Both methods, simplifying then converting, and direct conversion through division, yield the same result: 25%. Understanding this conversion is not merely an academic exercise; it's a practical skill with wide-ranging applications in everyday life and across various disciplines. By mastering this fundamental concept, you'll be better equipped to handle numerical information and make informed decisions in numerous situations. The underlying principle of proportionality ensures consistency and accuracy in these conversions, making percentages a powerful tool for representing and interpreting quantitative data.
Latest Posts
Latest Posts
-
Speed Of Light In Cm S
Sep 14, 2025
-
How Oz Is A Gallon
Sep 14, 2025
-
30 Fl Oz To Cups
Sep 14, 2025
-
Ave Maria Celine Dion Lyrics
Sep 14, 2025
-
What Is 80 Of 5
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.