200 Is 1 10 Of
scising
Sep 16, 2025 · 5 min read
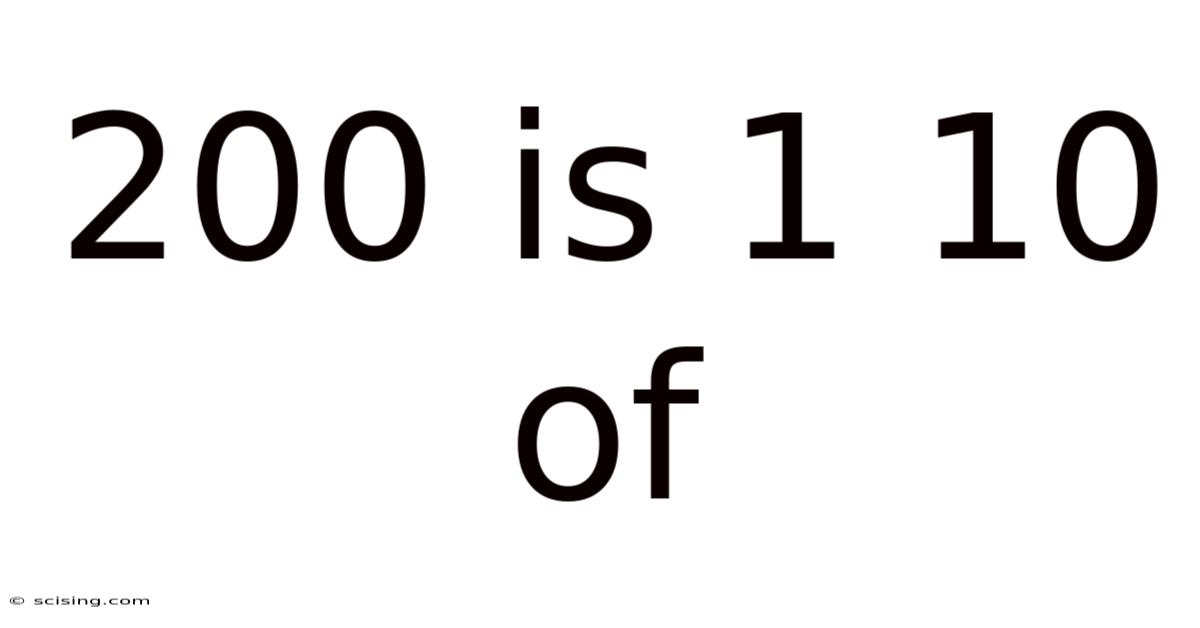
Table of Contents
200 is 1/10 of: Unveiling the Power of Proportions
Understanding proportions is a fundamental skill in mathematics, crucial for navigating various aspects of life, from cooking and construction to finance and scientific research. This article delves into the question: "200 is 1/10 of what number?" We'll explore the solution methodically, providing a clear explanation suitable for all levels of mathematical understanding. We’ll also examine the broader context of proportions, highlighting their practical applications and significance. This comprehensive guide will not only help you solve this specific problem but also equip you with the skills to tackle similar proportional relationships confidently.
Understanding the Problem: A Simple Proportion
The core of the problem lies in understanding the relationship between 200 and its fractional representation as 1/10 of a larger number. In simpler terms, we're looking for a number where 1/10 (or 10%) of that number is equal to 200. This is a classic example of a proportion, where two ratios are equal. We can represent this relationship mathematically as:
1/10 = 200/x
Where 'x' represents the unknown number we are trying to find.
Method 1: Solving the Proportion using Cross-Multiplication
One efficient way to solve this proportion is through cross-multiplication. This method involves multiplying the numerator of one fraction by the denominator of the other, and vice versa. Let's apply this to our equation:
1/10 = 200/x
Cross-multiplying, we get:
1 * x = 200 * 10
Simplifying, we find:
x = 2000
Therefore, 200 is 1/10 of 2000.
Method 2: Using the Decimal Equivalent
Another approach involves converting the fraction 1/10 into its decimal equivalent, which is 0.1. The problem can then be rephrased as:
0.1 * x = 200
To solve for 'x', we simply divide both sides of the equation by 0.1:
x = 200 / 0.1
This calculation yields:
x = 2000
Again, we arrive at the solution: 200 is 1/10 of 2000.
Method 3: Understanding Percentage
The fraction 1/10 is also equivalent to 10%. Therefore, the question can be reframed as:
"200 is 10% of what number?"
To solve this, we can use the formula for calculating percentages:
Percentage = (Part / Whole) * 100
In this case, we know the percentage (10%) and the part (200). We need to find the whole (x). Rearranging the formula, we get:
Whole (x) = (Part / Percentage) * 100
Substituting the values:
x = (200 / 10) * 100
x = 20 * 100
x = 2000
This method reinforces the solution: 200 is 10% (or 1/10) of 2000.
The Importance of Proportions in Real-World Applications
Understanding proportions is not confined to abstract mathematical problems; it's a crucial skill applied extensively in various fields. Here are some examples:
-
Cooking: Recipes often provide proportions for ingredients. If a recipe calls for 1/4 cup of sugar for 6 servings, and you want to make 12 servings, you'll need to double the amount of sugar, maintaining the correct proportion.
-
Construction and Engineering: Blueprints and architectural designs rely heavily on proportions to accurately scale buildings and structures. Accurate proportions ensure the structural integrity and functionality of the design.
-
Finance: Interest rates, loan calculations, and investment returns all involve proportional relationships. Understanding these proportions is vital for making informed financial decisions.
-
Science: Scientific experiments frequently involve precise measurements and proportions. Mixing chemicals, diluting solutions, and conducting experiments accurately depend on precise proportional calculations.
-
Mapmaking: Maps utilize scale, which is a form of proportion, to represent large geographical areas on smaller surfaces. Understanding the scale allows us to accurately determine distances and sizes on the map.
-
Graphic Design: Maintaining consistent proportions is crucial in graphic design to ensure visual harmony and balance in layouts and designs. The golden ratio, a specific mathematical proportion, is often employed in art and design for aesthetic appeal.
-
Data Analysis: Proportions are essential in analyzing data, particularly in calculating percentages, ratios, and rates. This is crucial in various fields like statistics, epidemiology, and market research.
Further Exploration: Understanding Ratios and Fractions
The problem "200 is 1/10 of what number?" highlights the interconnectedness of ratios and fractions. A ratio expresses the relative size of two or more values, while a fraction represents a part of a whole. In this case, the ratio of 200 to the unknown number is 1:10, and the fraction representing this ratio is 1/10.
Understanding these concepts allows for more flexible problem-solving approaches. For instance, you can visualize the problem as a fraction: 200 is one part out of ten equal parts, and you need to find the total value representing all ten parts.
Frequently Asked Questions (FAQ)
Q1: What if the fraction wasn't 1/10? How would I solve a similar problem with a different fraction?
A1: The same principles apply. If the problem was "200 is 2/5 of what number?", you would set up the proportion as 2/5 = 200/x and solve using cross-multiplication or other methods described above.
Q2: Can I use a calculator to solve these types of problems?
A2: Absolutely! Calculators can simplify the calculations involved, particularly when dealing with more complex fractions or decimals.
Q3: Are there any online resources or tools to help me practice solving proportions?
A3: Many online educational websites and apps offer interactive exercises and tutorials on solving proportions.
Q4: Why is understanding proportions important in everyday life?
A4: Proportions are fundamental to understanding and solving various real-world problems involving scaling, ratios, percentages, and comparisons. They underpin many practical tasks in various fields.
Conclusion: Mastering Proportions for a Brighter Future
The problem "200 is 1/10 of what number?" serves as a simple yet insightful introduction to the world of proportions. By understanding the methods to solve this problem – through cross-multiplication, decimal conversion, or percentage calculations – you gain a foundational understanding of a crucial mathematical concept with far-reaching applications. Mastering proportions is not just about solving mathematical equations; it’s about developing problem-solving skills applicable to countless real-world scenarios, enhancing your ability to analyze data, make informed decisions, and succeed in various fields. Remember that consistent practice and application are key to mastering this essential mathematical skill. So, continue exploring, experimenting, and applying these methods to various problems, and you’ll find that understanding proportions unlocks a wealth of opportunities and empowers you to tackle complex challenges with confidence.
Latest Posts
Latest Posts
-
Peter And Wendy Jm Barrie
Sep 16, 2025
-
Negative 3 Minus Negative 5
Sep 16, 2025
-
What Is A Grand Staff
Sep 16, 2025
-
Como Dibujar Estructuras De Resonancia
Sep 16, 2025
-
What Is 75 Of 40
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 200 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.