X Squared - 9 Factored
scising
Sep 19, 2025 · 5 min read
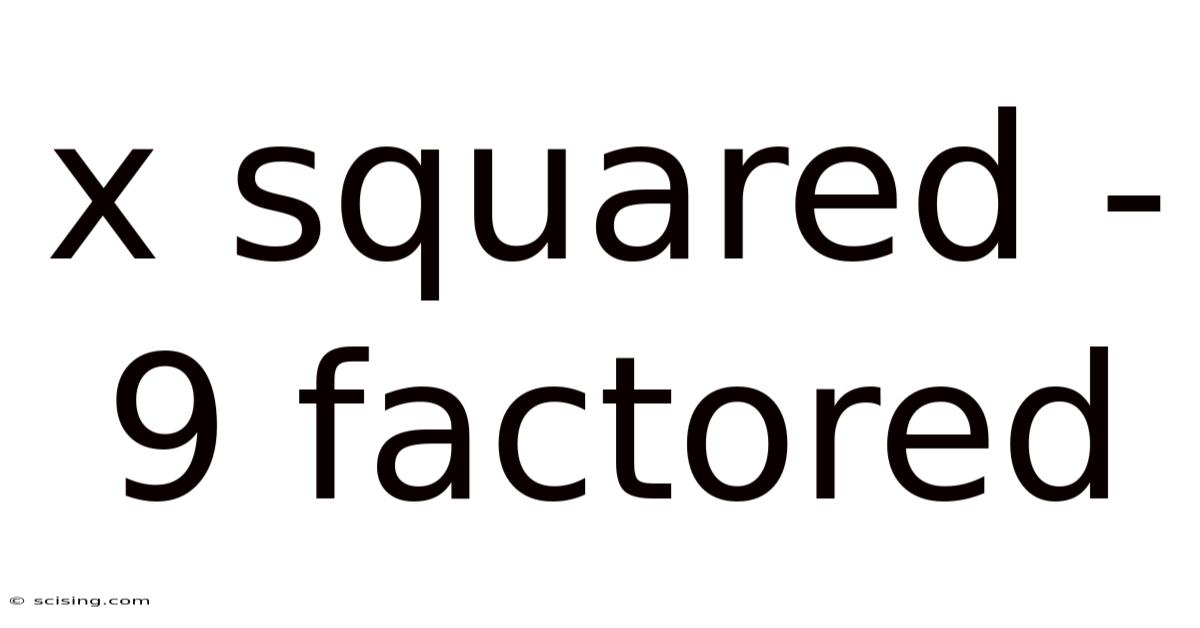
Table of Contents
Factoring x² - 9: A Deep Dive into Quadratic Expressions
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This article will thoroughly explore the factoring of x² - 9, explaining the process step-by-step, providing the underlying mathematical principles, and addressing common questions. We'll delve into different methods and show you how to apply this knowledge to similar problems, solidifying your understanding of algebraic manipulation. Mastering this will lay a strong foundation for more complex algebraic concepts.
Understanding Quadratic Expressions
Before we tackle factoring x² - 9, let's establish a basic understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0.
Our example, x² - 9, is a special case of a quadratic expression where b = 0 and c = -9. This specific form allows for a simpler factoring method than the general quadratic formula.
Factoring x² - 9: The Difference of Squares
x² - 9 is a perfect example of a difference of squares. A difference of squares is a binomial (a polynomial with two terms) that can be expressed as the difference between two perfect squares. The general form is a² - b², which factors to (a + b)(a - b).
Let's break down how this applies to x² - 9:
-
Identify the perfect squares: x² is the square of x (x² = x * x), and 9 is the square of 3 (9 = 3 * 3).
-
Apply the difference of squares formula: Using the formula a² - b² = (a + b)(a - b), where a = x and b = 3, we get:
x² - 9 = (x + 3)(x - 3)
Therefore, the factored form of x² - 9 is (x + 3)(x - 3). This means that if you were to expand (x + 3)(x - 3) using the FOIL method (First, Outer, Inner, Last), you would arrive back at x² - 9.
Verification Through Expansion
Let's verify our factored form using the FOIL method:
- First: x * x = x²
- Outer: x * -3 = -3x
- Inner: 3 * x = 3x
- Last: 3 * -3 = -9
Combining these terms, we get x² - 3x + 3x - 9. The -3x and +3x cancel each other out, leaving us with x² - 9, confirming our factoring is correct.
Why This Method Works: A Deeper Look
The difference of squares factorization is a consequence of the following algebraic identity:
(a + b)(a - b) = a² - ab + ab - b² = a² - b²
Notice how the 'ab' and '-ab' terms cancel each other out, leaving only the difference of squares. This is the key to the simplicity and efficiency of this factoring method. It elegantly exploits the properties of multiplication and addition/subtraction of algebraic expressions.
Applying the Difference of Squares to Other Problems
The difference of squares method isn't limited to x² - 9. It can be applied to any expression that fits the a² - b² pattern. Here are some examples:
-
4x² - 25: Here, a = 2x and b = 5. The factored form is (2x + 5)(2x - 5).
-
16y⁴ - 81: Here, a = 4y² and b = 9. The factored form is (4y² + 9)(4y² - 9). Notice that 4y² - 9 is itself a difference of squares and can be further factored.
-
x⁶ - y⁶: This can be factored multiple times using difference of squares:
- x⁶ - y⁶ = (x³ + y³)(x³ - y³).
- Both x³ + y³ and x³ - y³ can be further factored using the sum and difference of cubes formulas, respectively.
These examples highlight the versatility of the difference of squares method and its ability to simplify seemingly complex expressions.
What if it's Not a Difference of Squares?
It’s crucial to remember that the difference of squares method only works when you have a binomial that is the difference of two perfect squares. If you have a sum of squares (e.g., x² + 9), it generally cannot be factored using real numbers. This is a key distinction that many students initially find challenging to grasp.
Factoring with the Quadratic Formula (General Case)
While the difference of squares method is efficient for specific cases, the quadratic formula provides a more general approach for factoring any quadratic expression, including those where b ≠ 0. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
This formula gives you the roots (or zeros) of the quadratic equation ax² + bx + c = 0. Once you have the roots, say x₁ and x₂, you can factor the quadratic as a(x - x₁)(x - x₂).
However, for x² - 9 (where a = 1, b = 0, and c = -9), using the quadratic formula would be unnecessarily complex compared to the difference of squares method. The quadratic formula is more suitable for expressions where the middle term (bx) is present.
Frequently Asked Questions (FAQ)
Q1: Can x² - 9 be factored in any other way?
A1: While (x + 3)(x - 3) is the most straightforward and commonly used factorization, there aren't significantly different methods. Other approaches would ultimately lead to the same result.
Q2: What if the expression is x² + 9 instead of x² - 9?
A2: x² + 9, a sum of squares, is generally irreducible over real numbers. It cannot be factored using real numbers. However, it can be factored using complex numbers, resulting in (x + 3i)(x - 3i), where 'i' represents the imaginary unit (√-1).
Q3: How can I improve my factoring skills?
A3: Practice is key! Work through numerous examples, starting with simpler problems and gradually increasing the complexity. Focus on recognizing patterns and applying the appropriate factoring techniques. Understanding the underlying mathematical principles will improve your ability to solve more complex problems efficiently.
Q4: Are there online resources that can help me practice?
A4: Many online platforms offer practice problems and tutorials on factoring quadratic expressions.
Conclusion: Mastering Factorization
Factoring x² - 9, or any quadratic expression for that matter, is a critical skill in algebra and mathematics more broadly. This article has provided a thorough explanation of the difference of squares method, its application to various problems, and its underlying mathematical principles. Remember that understanding the "why" behind the methods is just as important as knowing "how" to apply them. By mastering these techniques, you will significantly enhance your ability to solve a wide range of algebraic problems and progress confidently in your mathematical studies. Consistent practice and a focus on understanding the underlying concepts are essential for achieving fluency and success in algebra.
Latest Posts
Latest Posts
-
Princess And The Pea Film
Sep 20, 2025
-
Money Weighted Rate Of Return
Sep 20, 2025
-
Map Of The Middle Colonies
Sep 20, 2025
-
Is The U S An Empire
Sep 20, 2025
-
Voluntary Manslaughter Vs Involuntary Manslaughter
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X Squared - 9 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.