X 6 X 4 X
scising
Sep 12, 2025 · 5 min read
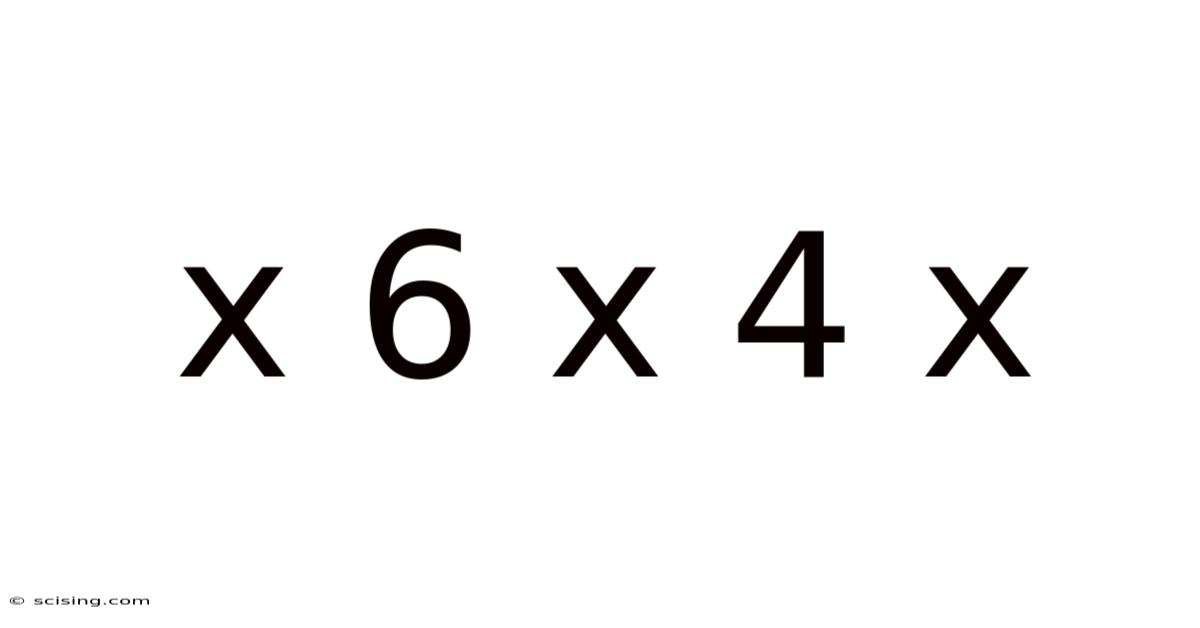
Table of Contents
Decoding the Mystery of X 6 X 4 X: Exploring Mathematical Concepts and Problem-Solving Strategies
This article delves into the intriguing mathematical expression "x 6 x 4 x," exploring its potential interpretations, the underlying mathematical concepts involved, and various problem-solving strategies to tackle such expressions. We will uncover the significance of variables, the order of operations (often remembered by the acronym PEMDAS/BODMAS), and how to approach similar problems with different variables and operators. Understanding these concepts is crucial for success in algebra and beyond.
Understanding the Expression: Variables and Operators
At first glance, "x 6 x 4 x" appears ambiguous. The key is recognizing the role of 'x' as a variable – a symbol representing an unknown value. The numbers 6 and 4 are constants, representing fixed values. The symbol 'x' also acts as a multiplication operator, signifying the multiplication operation between the variables and constants. This ambiguity highlights the importance of clear mathematical notation.
To solve this expression, we need to clarify the order in which these operations are performed. This is where the order of operations comes into play.
The Order of Operations: PEMDAS/BODMAS
The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictates the order of mathematical operations. Both acronyms represent the same fundamental principle:
-
Parentheses/Brackets: Calculations within parentheses or brackets are performed first. Our expression lacks parentheses, simplifying the process.
-
Exponents/Orders: Exponents (powers) are calculated next. Again, our expression doesn't involve exponents.
-
Multiplication and Division: These operations have equal precedence and are performed from left to right.
-
Addition and Subtraction: These operations also have equal precedence and are performed from left to right.
Solving the Expression: Different Interpretations and Approaches
The lack of clear operators between the 'x' and the numbers allows for multiple interpretations. Let's explore the most likely scenarios:
Scenario 1: Assuming Implicit Multiplication
If we assume the 'x's between the numbers represent implicit multiplication, the expression becomes:
x * 6 * x * 4 * x
This can be simplified to:
24x³
This means that the final result is 24 times the cube of the value represented by 'x'. For example:
- If x = 2, the expression equals 24 * 2³ = 24 * 8 = 192
- If x = 5, the expression equals 24 * 5³ = 24 * 125 = 3000
- If x = -1, the expression equals 24 * (-1)³ = 24 * (-1) = -24
Scenario 2: Considering a Polynomial Expression
Another interpretation could be to consider this as a simplified form of a polynomial expression, where the x's represent different variables:
Let's replace the x's with distinct variables, like this:
x₁ * 6 * x₂ * 4 * x₃
In this scenario, the expression becomes:
24x₁x₂x₃
The result depends on the values of x₁, x₂, and x₃. This interpretation introduces the concept of multiple variables, broadening the scope of the problem.
Scenario 3: Interpreting 'x' as an Unknown in an Equation
The expression could represent part of an equation. For instance:
x * 6 * x * 4 * x = 192
In this case, we have a cubic equation to solve:
24x³ = 192
Dividing both sides by 24:
x³ = 8
Taking the cube root of both sides:
x = 2
This demonstrates how the expression can be incorporated into a larger problem to solve for the unknown value of 'x'.
Expanding the Scope: More Complex Scenarios
The "x 6 x 4 x" expression provides a foundational example. Let's explore scenarios that increase in complexity:
-
Incorporating Parentheses: Adding parentheses changes the order of operations significantly. For example, (x * 6) * (x * 4) * x simplifies to 24x³. But (x * (6 * x)) * (4 * x) simplifies to 24x³. The placement of parentheses fundamentally alters the result.
-
Introducing Different Operators: Replacing the multiplication with addition, subtraction, or division will yield drastically different results.
-
Incorporating Exponents: Adding exponents adds another layer of complexity. For example, x⁶ * 4 * x² could be simplified to 4x⁸.
-
Solving Equations with Multiple Variables: Consider an equation like: x * 6 * y * 4 * z = 24xyz = k, where k is a constant. Solving for one variable requires knowing the values of the others.
The Importance of Clear Notation
These examples underscore the paramount importance of clear and unambiguous mathematical notation. Using parentheses, proper spacing, and consistent variable naming prevents ambiguity and ensures accurate calculations. The seemingly simple "x 6 x 4 x" illustrates the potential for misinterpretation if not addressed properly.
Problem-Solving Strategies: A Step-by-Step Approach
Solving mathematical expressions requires a systematic approach:
-
Identify the Operators and Variables: Clearly identify the operators (addition, subtraction, multiplication, division, exponents) and variables present in the expression.
-
Apply the Order of Operations (PEMDAS/BODMAS): Follow the order of operations to determine the sequence of calculations.
-
Simplify the Expression: Use algebraic rules to simplify the expression. This involves combining like terms, distributing terms, and applying other relevant techniques.
-
Solve for Unknowns (if applicable): If the expression forms part of an equation, use algebraic manipulation to solve for the unknown variable(s).
Frequently Asked Questions (FAQ)
Q: What is the most likely interpretation of "x 6 x 4 x"?
A: The most likely interpretation assumes implicit multiplication, resulting in the simplified expression 24x³. However, other interpretations are possible depending on the context.
Q: What is the difference between a constant and a variable?
A: A constant is a fixed value (e.g., 6, 4), while a variable represents an unknown value or a quantity that can change (e.g., x, y, z).
Q: Why is the order of operations important?
A: The order of operations ensures that everyone gets the same result when evaluating a mathematical expression. Without it, different people might obtain different answers.
Q: How can I improve my problem-solving skills in mathematics?
A: Practice is key! Work through a variety of problems, starting with simpler ones and gradually increasing the difficulty. Understand the underlying concepts and apply problem-solving strategies systematically.
Conclusion: Beyond the Basics
The seemingly simple expression "x 6 x 4 x" provides a springboard to explore fundamental concepts in algebra, including variables, constants, operators, the order of operations, and problem-solving strategies. Understanding these concepts builds a strong foundation for tackling more complex mathematical problems and furthering your mathematical journey. Remember, clear notation and a systematic approach are essential to success in mathematics. Mastering these skills empowers you to confidently decipher complex expressions and solve challenging equations.
Latest Posts
Latest Posts
-
Arabic Numbers 1 To 100
Sep 12, 2025
-
Hydrochloric Acid And Sodium Hydroxide
Sep 12, 2025
-
Asvab Scores For Navy Jobs
Sep 12, 2025
-
Piggy Chapter 8 Ship Chapter
Sep 12, 2025
-
Last Of The Mohicans Characters
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 6 X 4 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.