X 3 X 4 8
scising
Sep 07, 2025 · 5 min read
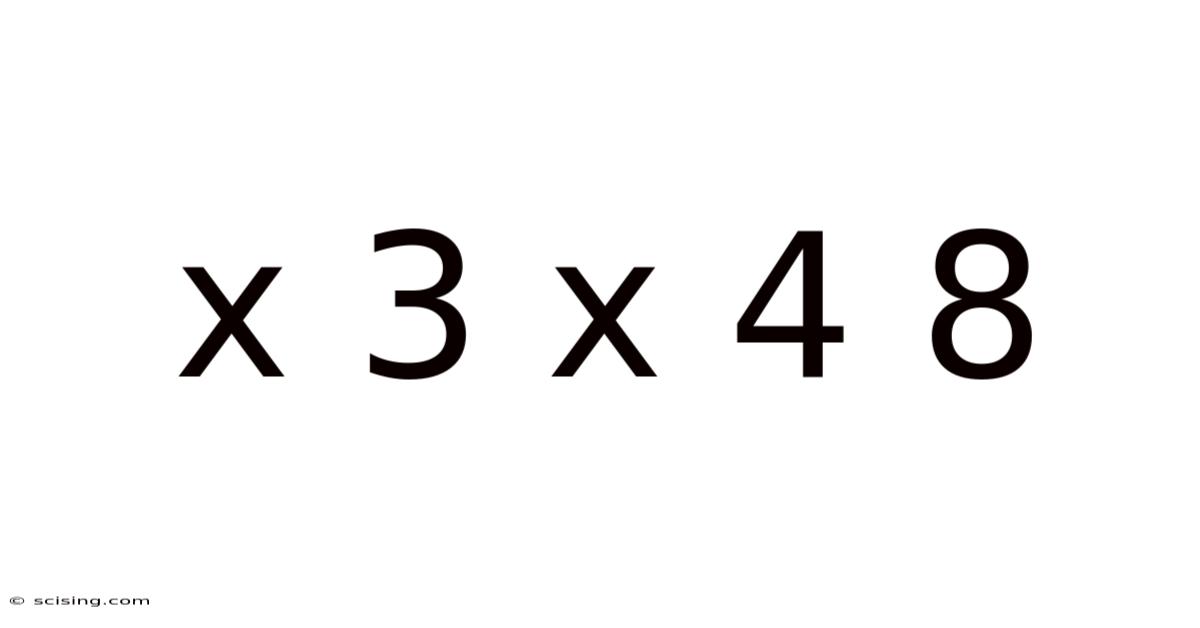
Table of Contents
Decoding the Mystery: Exploring the Mathematical Relationship of x³ x⁴ = 8
This article delves into the intriguing mathematical equation x³ x⁴ = 8, exploring its solution, the underlying principles, and its broader implications within algebra and beyond. We will dissect the problem step-by-step, providing a clear and comprehensive understanding for students of various mathematical backgrounds. Understanding this seemingly simple equation unlocks a deeper appreciation for fundamental algebraic concepts and problem-solving strategies. This exploration will move beyond a simple answer, delving into the reasoning, applications, and potential extensions of this problem.
Understanding the Problem: x³ x⁴ = 8
The equation x³ x⁴ = 8 presents a challenge that requires a solid understanding of exponents and algebraic manipulation. At its core, it asks: "What value of 'x' satisfies the equation where 'x' cubed multiplied by 'x' raised to the power of four equals 8?" This isn't just about finding a numerical answer; it's about mastering the process of solving exponential equations.
Step-by-Step Solution: Unraveling the Equation
The key to solving this equation lies in understanding the rules of exponents. Specifically, we'll use the rule of multiplying exponents with the same base: xᵃ xᵇ = x⁽ᵃ⁺ᵇ⁾.
-
Combining Exponents: Applying this rule to our equation, we can simplify the left-hand side:
x³ x⁴ = x⁽³⁺⁴⁾ = x⁷
-
Simplified Equation: Our equation now becomes significantly simpler:
x⁷ = 8
-
Finding the Seventh Root: To isolate 'x', we need to find the seventh root of both sides of the equation. This is the inverse operation of raising to the power of seven.
⁷√x⁷ = ⁷√8
-
Solution for x: This simplifies to:
x = ⁷√8
Now, while this is a mathematically correct solution, it's not expressed in a simplified, easily understandable form. We can explore this further.
Numerical Approximation and the Concept of Roots
The seventh root of 8 is not a whole number. It's an irrational number, meaning it cannot be expressed as a simple fraction. To find an approximate value, we can use a calculator or computer software. This gives us:
x ≈ 1.3459
This approximation highlights that the solution isn't a neat integer, which is a common occurrence in higher-order equations. It emphasizes the importance of understanding both exact and approximate solutions in mathematics.
Exploring the Equation Graphically
Visualizing the equation can provide further insight. If we were to graph the function y = x⁷ - 8, the solution to x⁷ = 8 would be the x-intercept (where the graph crosses the x-axis). The graph would clearly show that there is only one real solution, approximately 1.3459. This graphical representation reinforces the concept of a single real root for this equation.
The Complex Roots: Beyond the Real Numbers
While we've found one real solution, the equation x⁷ = 8 actually has seven solutions in the complex number system. This involves understanding complex numbers, which are numbers of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit (√-1).
Finding these complex roots requires a deeper understanding of complex number arithmetic and trigonometry, specifically utilizing De Moivre's Theorem. While this topic is beyond the scope of a basic introduction, it is crucial to note that many higher-order equations have solutions that extend beyond the realm of real numbers.
Expanding the Understanding: Applications and Extensions
The seemingly simple equation x³ x⁴ = 8 provides a stepping stone to understanding more complex mathematical concepts:
-
Polynomial Equations: This equation is a type of polynomial equation, specifically a seventh-degree polynomial equation. Solving these types of equations is a significant area of study in algebra, with various techniques and methods developed to tackle different types of polynomial equations.
-
Numerical Methods: When finding exact solutions becomes impractical, as with the seventh root of 8, numerical methods are employed to approximate the solutions. These methods involve iterative processes that progressively refine approximations until a desired level of accuracy is reached. Examples include the Newton-Raphson method and the bisection method.
-
Calculus and Optimization: In calculus, understanding equations like this forms the foundation for optimization problems. Finding the maximum or minimum values of functions frequently involves solving equations that are related to derivatives, leading to the necessity of understanding fundamental equation solving techniques.
Frequently Asked Questions (FAQs)
-
Q: Can this equation be solved using logarithms? A: Not directly. Logarithms are most effective for equations where the variable is part of the exponent. In this case, the variable is the base, making the root method more appropriate.
-
Q: Are there other ways to simplify x³ x⁴? A: Yes, you could expand the equation fully: x * x * x * x * x * x * x = 8. This emphasizes the multiplication involved but isn't as efficient as combining exponents.
-
Q: Why is it important to understand the complex roots? A: While the real root provides a practical solution in many scenarios, understanding the complete set of roots (including complex ones) is essential for a thorough understanding of the equation and its behavior in more advanced mathematical contexts. For instance, in electrical engineering, complex numbers are essential in analyzing alternating current circuits.
Conclusion: More Than Just an Equation
The equation x³ x⁴ = 8, though seemingly straightforward, serves as a potent example of fundamental mathematical principles. Solving this equation illustrates the importance of understanding exponent rules, the nuances of finding roots, and the existence of complex solutions. The journey beyond the simple numerical answer reveals the broader context within algebra and highlights the interconnectedness of various mathematical concepts. This deep dive not only provides the solution but also equips you with valuable problem-solving skills applicable in various mathematical fields and beyond. It emphasizes the importance of meticulous calculation and the exploration of solutions beyond simple arithmetic, highlighting the rich complexity hidden within seemingly basic mathematical problems.
Latest Posts
Latest Posts
-
How Much Is 50 Dimes
Sep 07, 2025
-
What Shapes Have Perpendicular Sides
Sep 07, 2025
-
Progressive Amendments To The Constitution
Sep 07, 2025
-
What Does Mis Prefix Mean
Sep 07, 2025
-
Three Types Of Point Mutations
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.