X 2 13x 36 0
scising
Sep 16, 2025 · 5 min read
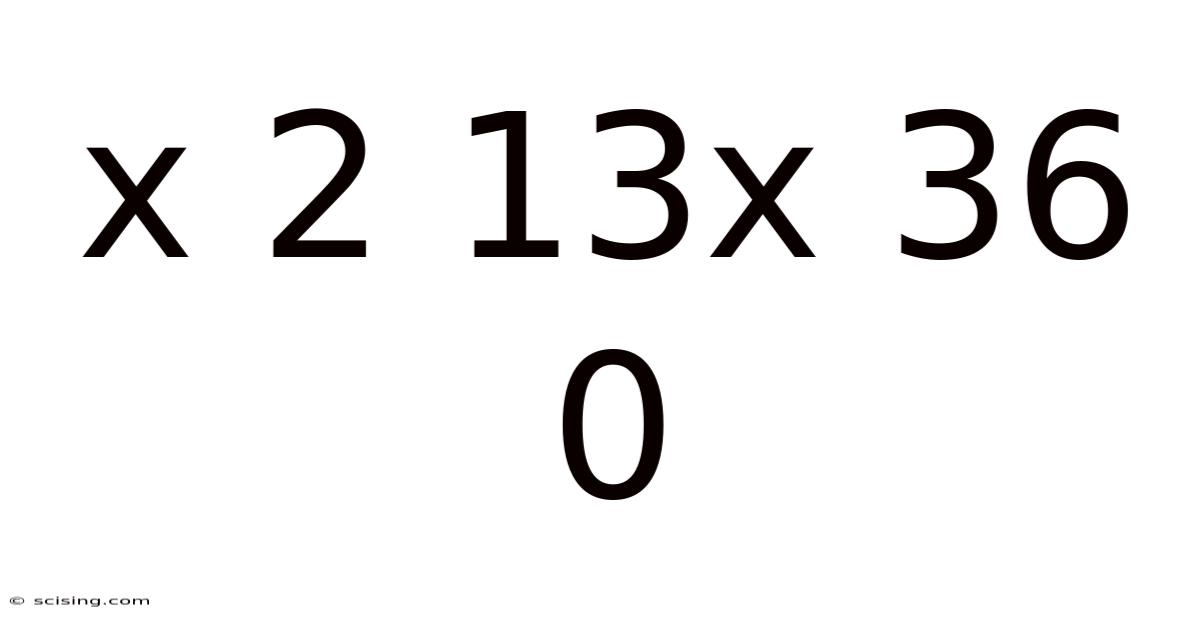
Table of Contents
Decoding the Sequence: x 2 13x 36 0 - A Deep Dive into Pattern Recognition and Mathematical Reasoning
This article explores the seemingly cryptic sequence "x 2 13x 36 0". We will delve into various methods of pattern recognition, mathematical reasoning, and problem-solving strategies to uncover the underlying logic and potential solutions. Understanding this sequence requires careful observation, logical deduction, and a willingness to consider multiple possibilities. This seemingly simple sequence offers a rich opportunity to explore fundamental mathematical concepts.
Understanding the Problem: What are we looking for?
The sequence "x 2 13x 36 0" presents a puzzle. The presence of "x" suggests a variable or an unknown quantity, requiring us to decipher its value or its role within the sequence. We need to identify the relationship between the elements (x, 2, 13x, 36, 0). Is there a consistent arithmetic progression, geometric progression, or a more complex pattern at play? Perhaps the sequence follows a recursive rule or involves a combination of different operations. The ultimate goal is to understand the principles governing the sequence and potentially predict future elements or find the value of 'x'.
Methods for Pattern Recognition: Exploring Different Avenues
Several approaches can help us decode this sequence:
-
Arithmetic Progression: We check for a constant difference between consecutive terms. However, the presence of 'x' immediately complicates this approach. The difference between 2 and 13x is not easily determined without knowing the value of 'x'. Similarly, the difference between 13x and 36 and between 36 and 0 is not immediately apparent.
-
Geometric Progression: We look for a constant ratio between consecutive terms. Again, the presence of 'x' makes this challenging. A constant ratio would imply that 2/x = 13x/36 = 36/0. This is impossible because division by zero is undefined.
-
Polynomial Relationships: We might consider if the terms are generated by a polynomial equation. A polynomial of degree higher than one could potentially account for the seemingly irregular sequence. However, finding a suitable polynomial to fit this sequence would require multiple equations, potentially leading to multiple solutions or no solution at all.
-
Algebraic Manipulation: Since 'x' is present, algebraic methods are crucial. We can explore relationships between the terms, setting up equations to try and solve for 'x'. We can look for factors or common multiples that might reveal a hidden pattern.
-
Combinatorial Methods: Certain sequences are governed by combinatorial principles, like permutations or combinations. However, this sequence doesn't appear to immediately relate to such concepts.
-
Modular Arithmetic: The sequence might exhibit patterns when considered modulo some integer. Modular arithmetic considers the remainders after division. We can investigate if reducing each term modulo a chosen integer reveals a consistent pattern. This might be particularly relevant if the numbers have some relation to prime numbers or other specific mathematical structures.
Algebraic Approaches: Solving for 'x'
Let's try several algebraic approaches, focusing on identifying potential relationships between the terms. Since we have a variable 'x', finding an equation or a set of equations involving 'x' is crucial.
Approach 1: Looking for Differences
Let's examine the differences between consecutive terms:
- 13x - 2
- 36 - 13x
- 0 - 36 = -36
We don't immediately see a clear relationship. However, we could attempt to set up equations based on the differences. For example, we could explore if 13x - 2 = k (some constant) and 36 - 13x = m (another constant), which would then require solving a system of two equations with two unknowns. This approach might not yield a unique solution but could still provide insights into potential relationships.
Approach 2: Exploring Ratios
While a geometric progression is unlikely due to the division by zero problem, we can still explore ratios between certain terms. However, this approach, like the difference approach, yields complex expressions with 'x' which would require further manipulation or solving of equations.
Approach 3: Considering the Position of the Terms
We can label each element with its position in the sequence:
- Position 1: x
- Position 2: 2
- Position 3: 13x
- Position 4: 36
- Position 5: 0
Exploring relationships based on position might reveal a pattern. Perhaps the terms are generated by a function of the position. This approach might involve polynomial fitting or other functional relationships.
Advanced Techniques: When Simple Approaches Fail
If the simpler methods prove fruitless, we might need to explore more sophisticated techniques:
-
Numerical Analysis: This branch of mathematics involves approximating solutions to numerical problems. If an analytical solution is elusive, numerical methods could provide approximate values for 'x'.
-
Computer Programming: A computer program could be used to test different patterns and relationships within the sequence, potentially identifying hidden structures or offering solutions that would be cumbersome to perform manually.
-
Pattern Recognition Algorithms: Specialized algorithms, used in machine learning and artificial intelligence, are designed to identify patterns in data. Such algorithms could be applied to this sequence to potentially identify underlying relationships not readily apparent to human observation.
The Importance of Context: Missing Information
It's crucial to acknowledge that the sequence "x 2 13x 36 0", without additional context, might not have a unique or definitive solution. More information is needed to fully understand its meaning and purpose. Where did this sequence come from? Is there a problem statement, a diagram, or additional instructions associated with it? Knowing the source could shed significant light on the intended pattern or meaning of the sequence.
Conclusion: A Journey into Mathematical Problem Solving
Decoding the sequence "x 2 13x 36 0" highlights the importance of systematic problem-solving and a multi-faceted approach to pattern recognition. While straightforward arithmetic or geometric progressions might not immediately apply, algebraic manipulation, and exploring various mathematical relationships remain valuable tools. The challenge underscores the fact that some mathematical puzzles require creativity, persistence, and the willingness to consider different approaches. Without further context, multiple solutions or no solution at all remain possibilities. The exploration, however, provides a valuable learning experience in mathematical reasoning and problem-solving techniques. The pursuit of understanding the underlying pattern fosters critical thinking and enhances our ability to tackle complex problems in diverse areas, beyond the realm of pure mathematics. The journey itself, even without a definitive answer, contributes significantly to strengthening analytical skills.
Latest Posts
Latest Posts
-
What Is Mg In Physics
Sep 16, 2025
-
Use Isolationism In A Sentence
Sep 16, 2025
-
The Monk From Canterbury Tales
Sep 16, 2025
-
Convert Fl Oz To Liter
Sep 16, 2025
-
What Is Church Of Christ
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 13x 36 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.