Whats 5 Percent Of 40
scising
Sep 15, 2025 · 5 min read
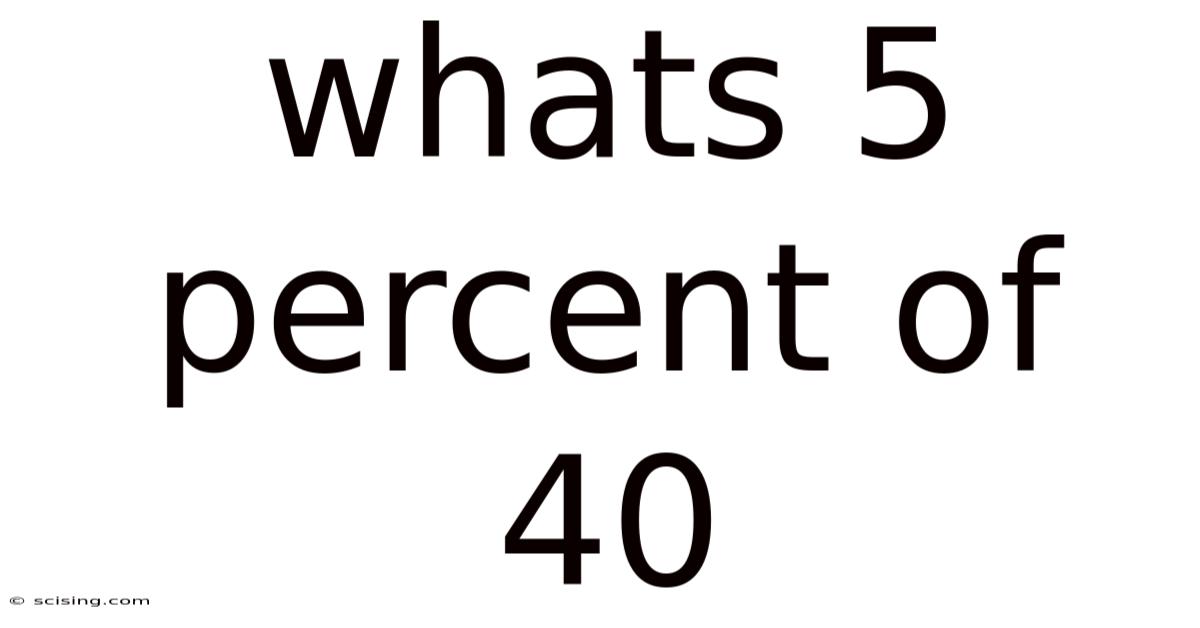
Table of Contents
What's 5 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 5 percent of 40 might seem like a simple calculation, easily solvable with a quick calculator search. But this seemingly basic problem opens a door to understanding a fundamental concept in mathematics and its widespread applications in everyday life, from calculating sales tax and discounts to understanding financial statements and statistical analyses. This article will not only answer the question "What's 5 percent of 40?" but will also explore the underlying principles of percentages, different methods for calculating them, and real-world examples demonstrating their significance.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 5 percent (written as 5%) means 5 out of every 100, or 5/100. This fraction can be simplified to 1/20. Understanding this foundational concept is key to tackling percentage problems.
Method 1: Using the Decimal Equivalent
The most straightforward way to calculate 5 percent of 40 is to convert the percentage to its decimal equivalent. To do this, we divide the percentage by 100. In this case:
5% / 100 = 0.05
Now, we simply multiply this decimal by the number we're finding the percentage of (40):
0.05 * 40 = 2
Therefore, 5 percent of 40 is 2.
Method 2: Using Fractions
As mentioned earlier, 5% can be expressed as the fraction 5/100, which simplifies to 1/20. Using this fraction, we can calculate 5 percent of 40 as follows:
(1/20) * 40 = 40/20 = 2
Again, we arrive at the answer: 5 percent of 40 is 2. This method highlights the interconnectedness between fractions, decimals, and percentages.
Method 3: Proportion Method
The proportion method offers a more visual approach to solving percentage problems. We set up a proportion, equating the ratio of the percentage to 100 with the ratio of the unknown value (x) to the total value (40):
5/100 = x/40
To solve for x, we cross-multiply:
100x = 5 * 40 100x = 200 x = 200/100 x = 2
This method reinforces the concept of proportional relationships, a vital concept in many areas of mathematics and science.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life. Here are some examples:
-
Sales and Discounts: Retail stores frequently offer discounts like "20% off." Understanding percentages allows consumers to quickly calculate the actual price reduction. For instance, a 20% discount on a $50 item would be 0.20 * $50 = $10, resulting in a final price of $40.
-
Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages. Knowing how to calculate these percentages is crucial for budgeting and financial planning. For example, a 6% sales tax on a $100 purchase would be 0.06 * $100 = $6.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is essential for making informed financial decisions. For example, a 5% interest rate on a $1000 loan would mean an annual interest payment of $50.
-
Tips and Gratuities: Calculating tips in restaurants and other service industries often involves percentages. A common tip is 15% or 20% of the bill.
-
Statistics and Data Analysis: Percentages are fundamental to interpreting and presenting statistical data. For example, expressing survey results as percentages helps to easily compare different groups or demographics.
Beyond the Basics: Advanced Percentage Calculations
While calculating 5 percent of 40 is a straightforward example, more complex percentage problems often arise. Here are some scenarios requiring a slightly more advanced understanding:
-
Calculating the Percentage Increase or Decrease: This involves determining the percentage change between two values. For example, if a stock price rises from $10 to $12, the percentage increase is calculated as: [(12-10)/10] * 100% = 20%.
-
Finding the Original Value: Sometimes, you know the percentage and the resulting value after a percentage increase or decrease, and you need to find the original value. This requires working backward using the percentage formula.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires understanding exponential growth and is crucial for long-term financial planning.
Frequently Asked Questions (FAQs)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include incorrectly converting percentages to decimals, performing incorrect order of operations in calculations, and misinterpreting the context of the problem. Careful attention to detail and a clear understanding of the underlying concepts are key to avoiding these errors.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online calculators are available for calculating percentages. These tools can be helpful for quick calculations, but understanding the underlying principles remains important.
Q: How can I improve my skills in calculating percentages?
A: Practice is essential. Start with simple problems and gradually progress to more complex ones. Understanding the different methods for calculating percentages (decimal, fraction, proportion) will enhance your problem-solving skills.
Conclusion: The Power of Understanding Percentages
The seemingly simple question "What's 5 percent of 40?" provides a launching point for a deeper exploration into the world of percentages. Mastering percentage calculations is not just about finding the answer to a specific problem; it's about gaining a fundamental understanding of a concept that underpins numerous aspects of our daily lives, from personal finance to professional endeavors. By grasping the different methods and their applications, you equip yourself with a valuable tool for navigating the complexities of the numerical world and making informed decisions in various contexts. Remember that while calculators can provide quick answers, a thorough understanding of the underlying principles ensures you'll be able to tackle even the most challenging percentage problems with confidence.
Latest Posts
Latest Posts
-
Is 0 A Finite Number
Sep 15, 2025
-
Is Earth Bigger Than Mars
Sep 15, 2025
-
Do It Snow In Jamaica
Sep 15, 2025
-
Food Web In The Desert
Sep 15, 2025
-
How To Get Expected Value
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.