Whats 30 Percent Of 500
scising
Sep 05, 2025 · 5 min read
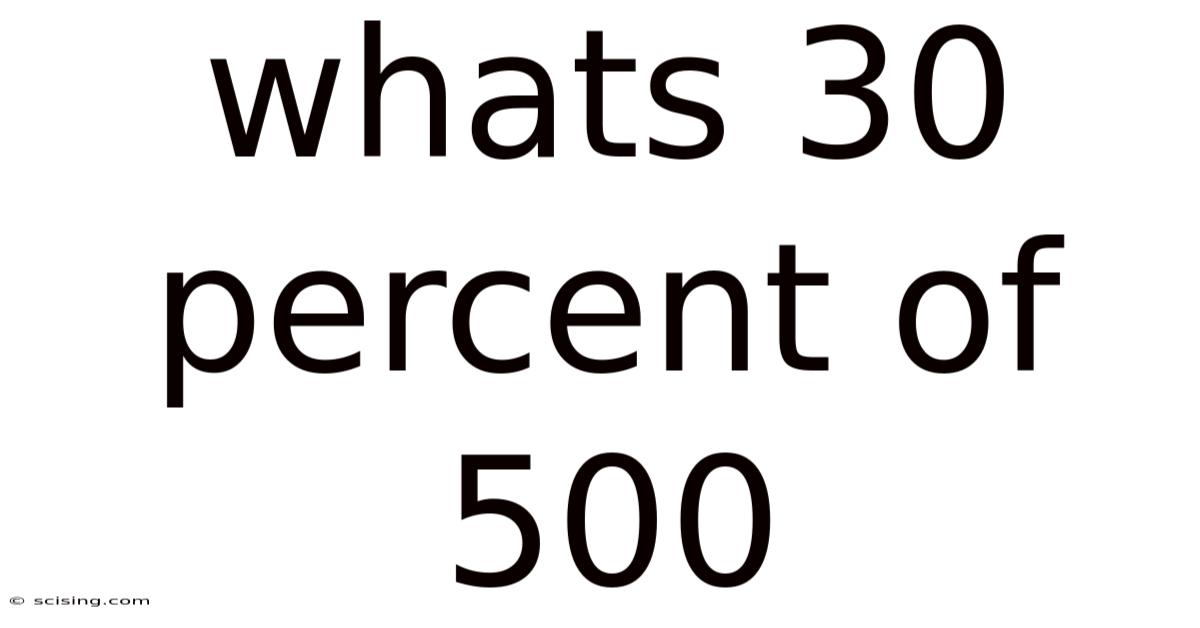
Table of Contents
What's 30 Percent of 500? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 500 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a world of practical applications in various fields, from everyday budgeting to complex financial modeling. This article will not only answer the question "What's 30 percent of 500?" but also explore the methods for calculating percentages, their real-world uses, and even delve into some related mathematical concepts.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred." So, 30% means 30 out of 100, or 30/100, which simplifies to 3/10. Understanding this fundamental concept is crucial for tackling percentage calculations.
Method 1: Using the Decimal Equivalent
The most straightforward method to calculate 30% of 500 involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. In this case:
30% ÷ 100 = 0.30
Now, multiply the decimal equivalent by the number you're finding the percentage of:
0.30 × 500 = 150
Therefore, 30% of 500 is 150.
Method 2: Using Fractions
As mentioned earlier, 30% can be expressed as the fraction 30/100. We can then use this fraction to calculate 30% of 500:
(30/100) × 500 = 150
This method highlights the direct relationship between percentages and fractions, reinforcing the fundamental concept. The calculation simplifies because 500 divided by 100 is 5, leaving us with 30 × 5 = 150.
Method 3: The Proportion Method
This method is particularly useful for solving more complex percentage problems. We set up a proportion:
x/500 = 30/100
Where 'x' represents the unknown value (30% of 500). To solve for 'x', we cross-multiply:
100x = 30 × 500
100x = 15000
x = 15000/100
x = 150
Again, we arrive at the answer: 30% of 500 is 150.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Financial Calculations: Calculating interest on loans, discounts on purchases, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding that a 10% discount on a $500 item saves you $50 requires a basic understanding of percentages.
-
Data Analysis and Statistics: Percentages are fundamental to representing and interpreting data. They're used to express proportions, rates, and changes in various statistical analyses, allowing for easy comparison and interpretation of data across different scales. For instance, understanding that 30% of a survey population prefers a particular brand helps gauge market share.
-
Scientific and Engineering Calculations: Percentages play a crucial role in various scientific and engineering applications. For instance, determining the efficiency of a machine or expressing the concentration of a chemical solution involves using percentage calculations.
-
Everyday Life: From calculating tips in restaurants to understanding sale prices in stores, percentages are embedded in our daily lives. Being able to quickly estimate percentages can save time and money.
Beyond the Basics: Working with More Complex Percentages
While calculating 30% of 500 is relatively simple, the same principles apply to more complex percentage calculations. Let's consider some variations:
-
Finding the original amount: If you know that 30% of a number is 150, you can work backward to find the original number. This involves using the formula: Original Number = (Percentage Amount) / (Percentage/100). In this case, 150 / (30/100) = 500.
-
Calculating percentage increase or decrease: Suppose a value increases from 500 to 650. To find the percentage increase, we first calculate the difference (650 - 500 = 150), then divide the difference by the original value (150/500 = 0.3), and finally multiply by 100 to express it as a percentage (0.3 × 100 = 30%). Therefore, there's a 30% increase.
-
Calculating percentages of percentages: These calculations involve applying percentages sequentially. For example, finding 10% of 30% of 500 would involve first finding 30% of 500 (150), and then finding 10% of 150 (15).
Percentage Calculations in Different Contexts
The method for calculating percentages remains consistent, but the context might influence the interpretation and application. Consider these examples:
-
Sales Tax: If the sales tax is 6%, and you buy an item costing 500, the tax amount would be 6% of 500, which is 30. The total cost would then be 500 + 30 = 530.
-
Discounts: A 20% discount on a 500 item results in a discount of 20% of 500, which is 100. The final price after the discount would be 500 - 100 = 400.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage of a number that is not a whole number?
A: The same methods apply. You would simply multiply the decimal equivalent of the percentage by the number, regardless of whether it's a whole number or a decimal.
Q: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, numerous online calculators are available to assist with percentage calculations, from simple percentage-of calculations to more complex percentage change and interest calculations.
Q: How can I improve my skills in calculating percentages quickly and efficiently?
A: Practice is key! Work through various problems, starting with simple ones and gradually increasing the complexity. Memorizing common percentage equivalents (e.g., 10% = 0.1, 25% = 0.25, etc.) can also improve your speed.
Conclusion
Calculating 30% of 500, while seemingly trivial, provides a gateway to understanding the broader application of percentages in various contexts. Mastering percentage calculations is a valuable skill that extends beyond the classroom, impacting various aspects of our personal and professional lives. Whether you're managing finances, analyzing data, or tackling complex problems in diverse fields, understanding percentages is a fundamental skill that unlocks opportunities and facilitates informed decision-making. Remember the three methods discussed – using decimal equivalents, fractions, and proportions – and choose the one that feels most intuitive and effective for you. With practice, you'll be able to tackle even the most complex percentage problems with confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.