Whats 30 Percent Of 40
scising
Sep 04, 2025 · 5 min read
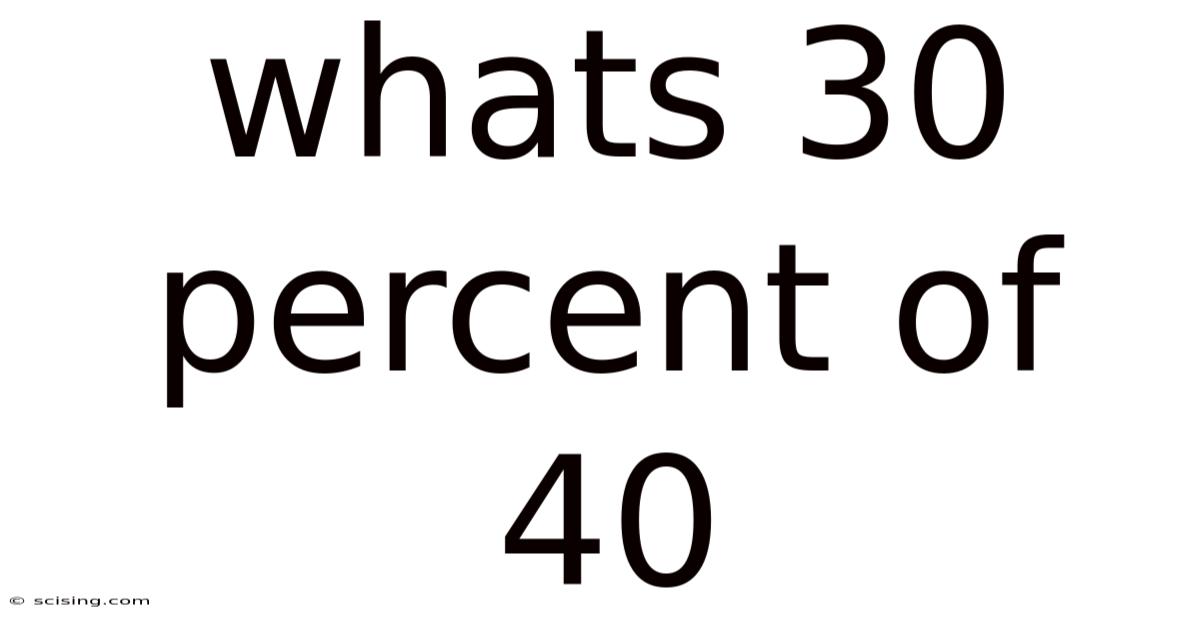
Table of Contents
What's 30 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 40 might seem like a simple calculation, and it is! But this seemingly straightforward question opens a door to understanding a fundamental mathematical concept with far-reaching applications in everyday life, from calculating discounts to understanding statistics and financial concepts. This article will not only answer the question "What's 30 percent of 40?" but also explore the underlying principles of percentages, different methods of calculation, and real-world examples of their use.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ("per cent" in Latin). So, 30 percent means 30 out of 100, or 30/100, which can be simplified to 3/10. This fraction represents a portion or proportion of a whole. Understanding this fundamental relationship is key to mastering percentage calculations.
Method 1: Using the Decimal Equivalent
The most straightforward method to calculate 30 percent of 40 is to convert the percentage to its decimal equivalent and then multiply. To convert a percentage to a decimal, simply divide the percentage by 100. Therefore:
30% = 30 ÷ 100 = 0.3
Now, multiply the decimal equivalent by the number you want to find the percentage of:
0.3 x 40 = 12
Therefore, 30 percent of 40 is 12.
Method 2: Using Fractions
As mentioned earlier, 30% can also be represented as the fraction 30/100, which simplifies to 3/10. We can use this fraction to calculate 30% of 40:
(3/10) x 40 = (3 x 40) / 10 = 120 / 10 = 12
Again, we arrive at the answer: 30 percent of 40 is 12. This method is particularly useful when dealing with simpler percentages that have easily reducible fractions.
Method 3: The Proportion Method
This method uses the concept of proportions to solve for the unknown value. We can set up a proportion like this:
30/100 = x/40
Where 'x' represents 30% of 40. To solve for x, we can cross-multiply:
30 x 40 = 100x
1200 = 100x
x = 1200 / 100
x = 12
So once again, 30 percent of 40 is 12. This method is helpful in understanding the underlying relationship between the percentage, the whole, and the part.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in various aspects of daily life and professional settings. Here are some examples:
-
Sales and Discounts: Imagine a store offering a 30% discount on a $40 item. Using the methods described above, you can quickly determine that the discount is $12, and the final price would be $28 ($40 - $12).
-
Taxes: Calculating sales tax or income tax involves understanding and applying percentages. If the sales tax in your area is 6%, you can easily calculate the tax amount on a purchase.
-
Tips and Gratuities: When dining out, calculating a tip (e.g., 15% or 20% of the bill) requires percentage calculations.
-
Financial Investments: Understanding interest rates (which are expressed as percentages) is vital for managing personal finances and making investment decisions. Compound interest, a crucial concept in finance, relies heavily on percentage calculations.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions, probabilities, and changes in data. For instance, understanding the percentage change in a company's stock price over time requires percentage calculations.
-
Scientific Research: Many scientific studies involve collecting and analyzing data, and percentages are frequently used to express the results and draw conclusions.
Beyond the Basics: More Complex Percentage Problems
While finding 30% of 40 is relatively simple, percentage calculations can become more complex. Consider scenarios where you need to:
-
Calculate the percentage increase or decrease: This involves finding the difference between two numbers and expressing it as a percentage of the original number.
-
Find the original number given a percentage and the resulting value: This often involves working backwards using the percentage and the final result to determine the initial value.
-
Solve problems involving multiple percentages: This might involve calculating a series of discounts or applying multiple taxes.
Mastering these more advanced percentage calculations requires a solid understanding of the foundational concepts explored in this article. Practice is key to developing proficiency.
Frequently Asked Questions (FAQs)
Q: What if I need to calculate a different percentage of 40, say 15%?
A: You would use the same methods described above, substituting 15% (or 0.15 as a decimal and 15/100 as a fraction) for 30%. 15% of 40 is (0.15 x 40) = 6.
Q: How can I calculate percentages quickly without a calculator?
A: For some percentages, mental math tricks can be helpful. For example, 10% of a number is simply the number divided by 10. 5% is half of 10%, and so on. Practicing mental math techniques can significantly improve your speed and accuracy in calculating percentages.
Q: Are there online calculators or tools that can help with percentage calculations?
A: Yes, many online calculators are available specifically designed for percentage calculations. These can be particularly helpful for more complex problems. However, understanding the underlying principles remains essential.
Q: Why is it important to understand percentages?
A: Understanding percentages is crucial for everyday life, personal finance, and many professional fields. It's a fundamental mathematical skill that enables you to interpret data, make informed decisions, and solve problems in a variety of contexts.
Conclusion: Mastering the Power of Percentages
While the answer to "What's 30 percent of 40?" is simply 12, the journey to arrive at this answer has unveiled the broader significance of percentages. From simple discounts to complex financial models, percentages are an indispensable tool. This article has equipped you not only with the methods to calculate percentages but also with a deeper understanding of their application in various contexts. By mastering this fundamental mathematical skill, you empower yourself to navigate the numerical world with confidence and competence. Continue practicing and exploring the various applications of percentages – you'll be surprised by how often this seemingly simple concept comes into play in your daily life.
Latest Posts
Latest Posts
-
What Is A Business Domain
Sep 04, 2025
-
Is Hcl An Ionic Compound
Sep 04, 2025
-
What Is A Parametric Function
Sep 04, 2025
-
22 Inches How Many Feet
Sep 04, 2025
-
Journey To The West Synopsis
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.