Whats 25 Percent Of 1000
scising
Sep 12, 2025 · 5 min read
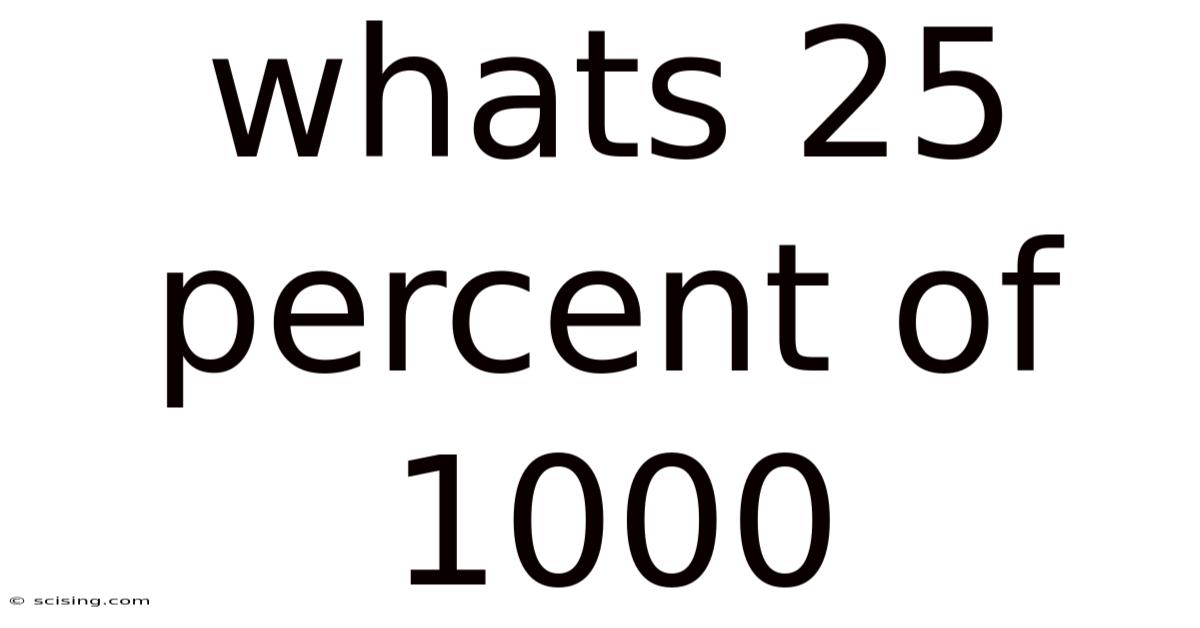
Table of Contents
What's 25 Percent of 1000? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 1000 is a seemingly simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This article will not only answer that question directly but will also explore the broader meaning of percentages, different methods for calculating them, and their widespread applications in various fields. We'll delve into the theory, show you multiple ways to solve the problem, and even look at some real-world examples to solidify your understanding. By the end, you’ll be confident in calculating percentages and applying this knowledge to various scenarios.
Understanding Percentages: The Basics
A percentage is simply a fraction where the denominator is always 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." So, 25 percent (often written as 25%) means 25 out of 100, or 25/100. This can be represented as a decimal (0.25) or a fraction (1/4). Understanding these different representations is crucial for efficient percentage calculations.
Calculating 25% of 1000: The Simple Approach
The most straightforward way to find 25% of 1000 is to convert the percentage to a decimal and multiply:
- Convert the percentage to a decimal: 25% = 0.25 (divide the percentage by 100)
- Multiply the decimal by the number: 0.25 * 1000 = 250
Therefore, 25% of 1000 is 250.
Alternative Methods: Exploring Different Approaches
While the above method is efficient, let's explore other approaches to reinforce our understanding and demonstrate the flexibility of percentage calculations.
Method 2: Using Fractions
Since 25% is equivalent to 1/4, we can use this fraction to calculate:
- Represent the percentage as a fraction: 25% = 1/4
- Multiply the fraction by the number: (1/4) * 1000 = 1000/4 = 250
This method confirms our previous result: 25% of 1000 is 250.
Method 3: Proportion Method
This method utilizes the concept of proportions, setting up an equation to solve for the unknown value:
- Set up a proportion: 25/100 = x/1000 (where x represents 25% of 1000)
- Cross-multiply: 25 * 1000 = 100 * x
- Solve for x: 25000 = 100x => x = 25000/100 = 250
Again, we arrive at the same answer: 25% of 1000 is 250.
Beyond the Basics: Understanding the Practical Applications
The ability to calculate percentages isn't just an academic exercise; it's a vital skill with numerous real-world applications. Let's explore some examples:
1. Sales and Discounts:
Imagine a store offering a 25% discount on a $1000 item. Using our knowledge, we know the discount amount is $250, making the final price $750. This is a common scenario in retail, requiring an understanding of percentage calculations to determine savings and final costs.
2. Taxes and Interest:
Calculating sales tax or interest on loans often involves percentages. If a 5% sales tax is applied to a $1000 purchase, the tax amount would be $50 (5% of 1000). Similarly, understanding interest calculations is essential for managing personal finances and investments.
3. Statistics and Data Analysis:
Percentages are fundamental in statistics. Representing data as percentages helps to visualize proportions and trends within datasets. For example, if a survey shows that 25% of 1000 respondents prefer a particular product, it represents 250 respondents. This information can be crucial for market research and decision-making.
4. Profit Margins and Financial Analysis:
Businesses use percentage calculations to determine profit margins, analyzing the profitability of their products and services. If a company's profit is 25% of its $1000 revenue, its profit would be $250. This is a key indicator of financial health and efficiency.
5. Tip Calculation:
Calculating tips at restaurants often involves percentages. A 25% tip on a $1000 bill would be $250. This simple calculation ensures fair compensation for service providers.
Advanced Percentage Calculations: Tackling More Complex Scenarios
While 25% of 1000 is a straightforward calculation, let’s briefly touch upon more complex scenarios that involve percentages:
Calculating the Percentage Increase or Decrease:
Suppose a value increases from 1000 to 1250. To calculate the percentage increase:
- Find the difference: 1250 - 1000 = 250
- Divide the difference by the original value: 250 / 1000 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
Therefore, there is a 25% increase. A similar approach is used to calculate percentage decreases.
Finding the Original Value from a Percentage and Result:
Imagine knowing that 25% of an unknown value is 250. To find the original value:
- Convert the percentage to a decimal: 25% = 0.25
- Divide the result by the decimal: 250 / 0.25 = 1000
This confirms our original value was 1000.
Frequently Asked Questions (FAQ)
Q1: What are some common mistakes people make when calculating percentages?
- Incorrect decimal conversion: Failing to accurately convert percentages to decimals is a common error. Remember to divide the percentage by 100.
- Mixing up the order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving percentages.
- Incorrectly applying percentage increases/decreases: Carefully consider whether you're calculating an increase or decrease and use the correct formula.
Q2: Are there any online tools or calculators for percentage calculations?
Yes, numerous online percentage calculators are readily available, offering assistance with various percentage-related calculations. These tools can be particularly helpful for more complex calculations.
Q3: How can I improve my skills in calculating percentages?
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use different methods: Familiarize yourself with multiple approaches (decimal, fraction, proportion) to reinforce your understanding.
- Apply it to real-world scenarios: Relate percentage calculations to everyday situations to solidify your practical skills.
Conclusion: Mastering Percentages for Real-World Success
Calculating 25% of 1000, while seemingly simple, provides a strong foundation for understanding percentages and their applications. We’ve explored various methods, highlighted real-world examples, and touched upon more advanced concepts. Mastering percentage calculations is a crucial skill, empowering you to navigate various aspects of daily life, from personal finance to professional settings. By understanding the underlying principles and practicing regularly, you can confidently tackle percentage problems and apply this knowledge to solve real-world challenges. Remember that consistent practice is key to mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Colours That Rhyme With Blue
Sep 12, 2025
-
Lady Jane Grey Last Words
Sep 12, 2025
-
What Is The Molecular Compound
Sep 12, 2025
-
The Nightingale And The Rose
Sep 12, 2025
-
Secondary Consumers In The Desert
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.