What Is Half Of 3.5
scising
Sep 23, 2025 · 4 min read
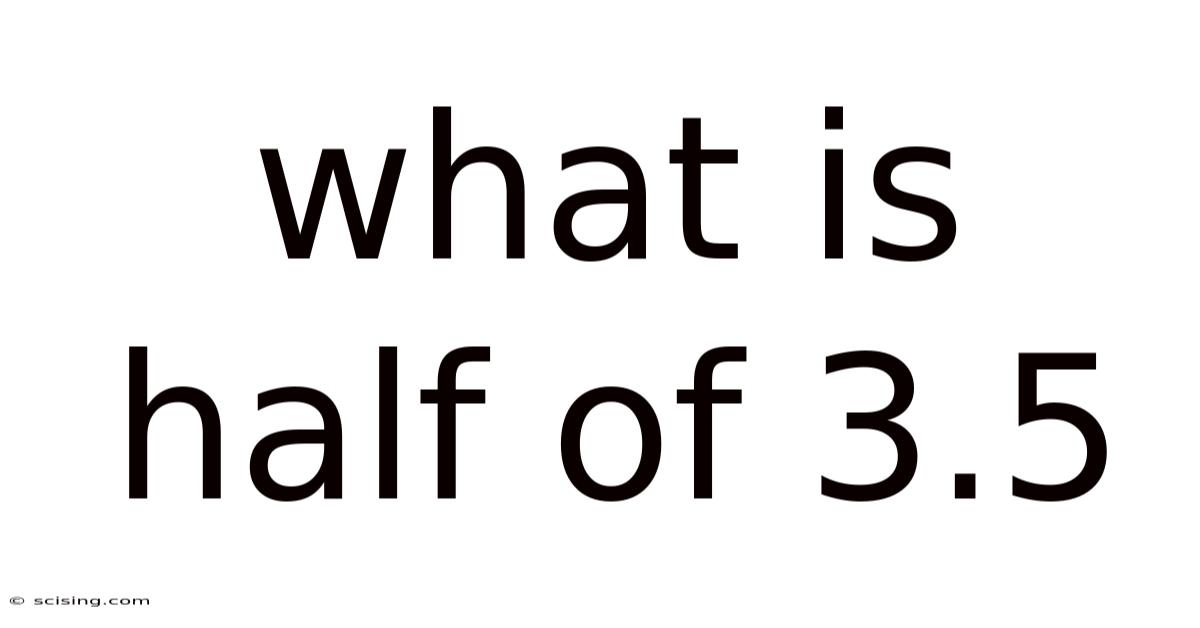
Table of Contents
What is Half of 3.5? A Deep Dive into Fractions, Decimals, and Division
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life and advanced calculations. This article explores the seemingly simple question, "What is half of 3.5?", delving into the various methods for solving it, the underlying mathematical principles, and expanding upon the broader context of fractions and decimals. We'll unpack the process, providing a comprehensive understanding accessible to all, regardless of mathematical background.
Understanding the Problem: Half, Fractions, and Decimals
The question, "What is half of 3.5?", essentially asks us to calculate half of 3.5, or 3.5 divided by 2. This involves understanding two key mathematical concepts:
-
Fractions: A fraction represents a part of a whole. Half, represented as ½ or 0.5, signifies one of two equal parts.
-
Decimals: Decimals are another way to represent fractions, using a base-ten system. The number 3.5 represents three whole units and five-tenths of a unit.
Method 1: Division
The most straightforward method is to divide 3.5 by 2:
3.5 ÷ 2 = 1.75
Therefore, half of 3.5 is 1.75.
Method 2: Converting to Fractions
We can convert the decimal 3.5 into a fraction and then find half:
-
Convert 3.5 to a fraction: 3.5 can be written as 3 5/10, which simplifies to 3 ½ or 7/2.
-
Find half of the fraction: (7/2) ÷ 2 = 7/4
-
Convert the fraction back to a decimal: 7/4 = 1.75
This method reinforces the relationship between fractions and decimals, illustrating their interchangeability in mathematical operations.
Method 3: Visual Representation
Imagine a number line representing the value 3.5. To find half of it, we can visually divide the line into two equal parts. The midpoint would fall precisely at 1.75. This visual approach helps build an intuitive understanding of the concept of halving. The visualization is incredibly useful when working with smaller values or when introducing this concept to children.
Expanding the Concept: Beyond Halving 3.5
While the core question focuses on 3.5, understanding the principles allows us to extend this to other numbers. Let's explore some related concepts:
-
Finding a third of a number: To find one-third of a number, we divide it by 3. For example, one-third of 3.5 is approximately 1.1667.
-
Finding other fractions of a number: Similar principles apply for any fraction. To find a fraction x/y of a number n, we calculate (x/y) * n.
-
Working with larger numbers: The methods described above apply equally to larger numbers. Finding half of 100, for instance, involves dividing 100 by 2 to get 50.
-
Working with different bases: Although we primarily use base-10 (decimal) in this example, the concept of halving applies across different number systems.
Real-World Applications of Finding Half
The seemingly simple act of finding half has countless real-world applications:
-
Sharing: Dividing resources or tasks equally among two people. For example, splitting a bill at a restaurant.
-
Measurement: Converting units, such as halving a recipe or determining the midpoint of a distance.
-
Cooking: Adjusting recipe sizes to accommodate a smaller number of servings.
-
Construction: Calculating dimensions and materials for projects.
-
Finance: Determining percentages and splitting costs or profits.
-
Programming: In computer science, the process of halving values (often done recursively) is fundamental to algorithms like binary search.
-
Data Analysis: Calculations involving proportions and averages frequently involve finding fractions of larger data sets.
Mathematical Principles at Play
The process of finding half of 3.5 illustrates several core mathematical principles:
-
Division: The fundamental operation used to find a fraction of a number.
-
Fractions and Decimals: The ability to represent numbers in different formats and seamlessly switch between them.
-
Equivalence: Demonstrates how fractions and decimals can represent the same value (e.g., 1.75 and 7/4).
-
Proportions: Understanding the relationship between parts and wholes.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to find half of 3.5? A: Absolutely! Calculators provide a quick and accurate way to perform the division.
-
Q: Is there a difference between dividing 3.5 by 2 and multiplying 3.5 by 0.5? A: No, both calculations yield the same result (1.75). Multiplying by 0.5 is simply another way of expressing division by 2.
-
Q: What if I need to find half of a larger decimal number, like 37.5? A: The same principles apply; simply divide 37.5 by 2. The answer would be 18.75.
-
Q: How do I explain this concept to a child? A: Use visual aids, like dividing a pizza or a group of objects into two equal parts.
Conclusion: Mastering the Fundamentals
Finding half of 3.5, while seemingly simple, provides a gateway to understanding fundamental mathematical concepts, including division, fractions, decimals, and their real-world applications. Mastering these principles builds a solid foundation for more advanced mathematical concepts and problem-solving in various fields. The ability to quickly and accurately calculate fractions of numbers is a highly valuable skill with applications spanning across numerous aspects of daily life and various professional domains. Remember, practice makes perfect; the more you work with these concepts, the more intuitive and effortless they become. So, next time you encounter a problem involving fractions, approach it with confidence, knowing the power and versatility of these fundamental mathematical tools.
Latest Posts
Latest Posts
-
How Heavy Is An Ounce
Sep 23, 2025
-
What Is An Electron Group
Sep 23, 2025
-
Food Chain With A Lion
Sep 23, 2025
-
Seven Commandments In Animal Farm
Sep 23, 2025
-
Radioactive Elements On Periodic Table
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.