What Is 80 Of 180
scising
Sep 08, 2025 · 5 min read
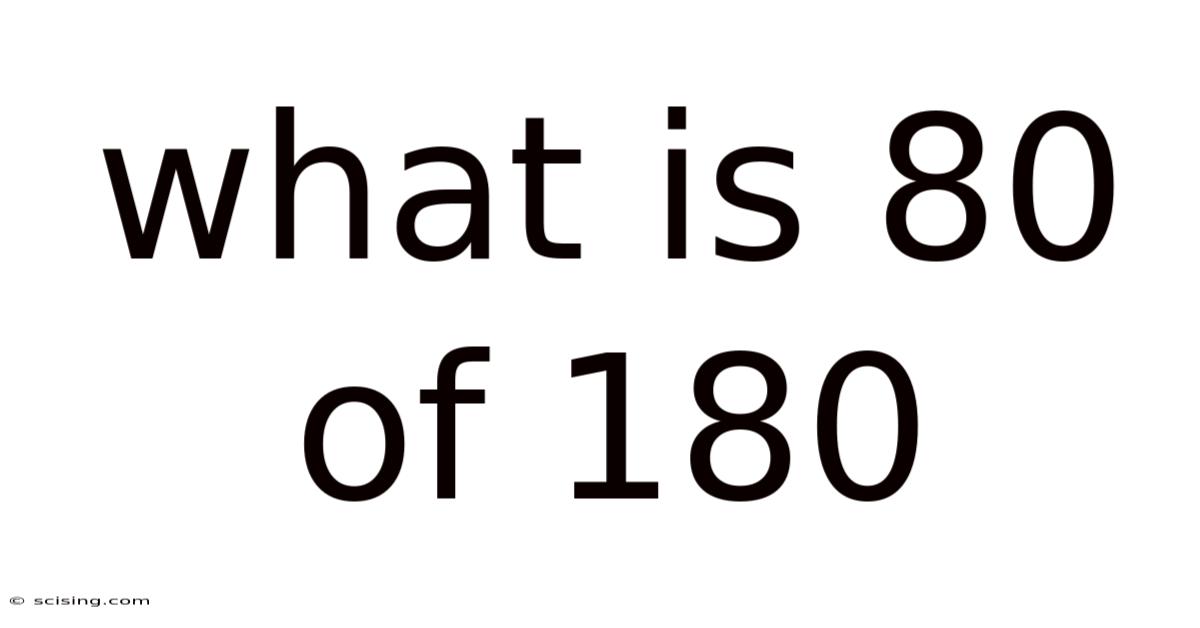
Table of Contents
What is 80% of 180? A Deep Dive into Percentages and Their Applications
Finding 80% of 180 might seem like a simple arithmetic problem, but it opens a door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer the question directly but also delve into the underlying principles of percentages, explore different methods for calculation, and illustrate its relevance in real-world scenarios. We'll cover everything from basic arithmetic to more advanced percentage-related problems, making this a comprehensive guide for anyone wanting to grasp this important concept.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred." Therefore, 80% means 80 out of 100, or 80/100. This can be simplified to 4/5. Understanding this fundamental relationship is key to solving any percentage problem.
Method 1: The Direct Calculation Approach
The most straightforward method to find 80% of 180 involves converting the percentage to a decimal and then multiplying it by the given number.
- Step 1: Convert the percentage to a decimal: To convert 80% to a decimal, divide it by 100: 80/100 = 0.8
- Step 2: Multiply the decimal by the number: Multiply 0.8 by 180: 0.8 * 180 = 144
Therefore, 80% of 180 is 144.
Method 2: The Fraction Approach
As mentioned earlier, 80% can be represented as the fraction 80/100 or its simplified form, 4/5. This approach uses this fractional representation for calculation.
- Step 1: Represent the percentage as a fraction: 80% = 80/100 = 4/5
- Step 2: Multiply the fraction by the number: Multiply 4/5 by 180: (4/5) * 180 = (4 * 180) / 5 = 720 / 5 = 144
This method again confirms that 80% of 180 is 144.
Method 3: Using Proportions
Proportions offer another effective way to solve percentage problems. This method sets up a ratio to find the unknown value.
- Step 1: Set up a proportion: We can set up the proportion as follows: x/180 = 80/100, where 'x' represents the unknown value (80% of 180).
- Step 2: Cross-multiply: Cross-multiplying gives us 100x = 80 * 180 = 14400
- Step 3: Solve for x: Divide both sides by 100: x = 14400 / 100 = 144
This reinforces the answer: 80% of 180 is 144.
Real-World Applications of Percentages
The concept of finding a percentage of a number is incredibly versatile and applies to numerous real-life situations:
- Sales and Discounts: Stores frequently advertise discounts as percentages. For example, a 20% discount on a $100 item means you save 20% of $100, which is $20, resulting in a final price of $80.
- Taxes: Sales tax is calculated as a percentage of the purchase price. If the sales tax is 6%, and you buy an item for $50, you'll pay an additional 6% of $50, which is $3, making the total cost $53.
- Interest Rates: Interest on loans or savings accounts is expressed as a percentage. Understanding percentage calculations is crucial for comprehending the cost of borrowing or the returns on your savings.
- Grade Calculations: In many educational systems, grades are expressed as percentages. For instance, a score of 85 out of 100 translates to an 85% grade.
- Statistics and Data Analysis: Percentages are fundamental to representing and analyzing data. They help in visualizing proportions and trends within datasets. For example, understanding voter turnout percentages is essential for political analysis.
- Tip Calculations: Restaurants often recommend tipping a certain percentage of the bill, which requires calculating the percentage of the total amount. A 15% tip on a $75 bill is 15% of $75 = $11.25.
Expanding on Percentage Calculations: More Complex Scenarios
While finding 80% of 180 is a relatively straightforward calculation, let's explore some more complex scenarios involving percentages:
- Finding the original value: Imagine you bought an item on sale for $90, which was a 10% discount. To find the original price, you would need to solve the equation: 0.9x = 90, where 'x' is the original price. Solving for x gives you x = 100. The original price was $100.
- Calculating percentage increase or decrease: Suppose a company's revenue increased from $100,000 to $120,000. To calculate the percentage increase, first find the difference ($20,000), then divide it by the original amount ($100,000), and finally multiply by 100%: ($20,000 / $100,000) * 100% = 20%. The revenue increased by 20%.
- Compound Interest: Compound interest calculations involve applying interest to both the principal amount and accumulated interest from previous periods. This requires multiple percentage calculations, making it a more advanced application.
- Percentage Points vs. Percentage Change: It is crucial to differentiate between percentage points and percentage change. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage that isn't a whole number, such as 37.5%?
A: The same principles apply. Convert 37.5% to a decimal (0.375) and multiply it by the given number.
-
Q: Are there any shortcuts for calculating percentages mentally?
A: For certain percentages, mental shortcuts exist. For example, 10% is simply moving the decimal point one place to the left. 5% is half of 10%. These shortcuts can make estimations quicker.
-
Q: How can I improve my understanding of percentages?
A: Practice is key! Solve various percentage problems of increasing complexity. Online resources, workbooks, and educational videos can provide further assistance.
-
Q: Can I use a calculator for percentage calculations?
A: Absolutely! Calculators are valuable tools for quick and accurate percentage calculations, especially for more complex problems. Many calculators have a percentage key (%) that simplifies the process.
Conclusion
Finding 80% of 180, which equals 144, is a basic yet crucial percentage calculation. This article has explored various methods for calculating percentages and highlighted their relevance across numerous real-world applications. Mastering percentage calculations is an essential skill for anyone navigating financial transactions, data analysis, or various academic disciplines. By understanding the fundamental concepts and practicing different approaches, you can confidently tackle percentage problems of any complexity. Remember, consistent practice and exploration of diverse applications will strengthen your understanding and improve your problem-solving abilities in this vital area of mathematics.
Latest Posts
Latest Posts
-
Hindu God With 6 Arms
Sep 08, 2025
-
What Equals 108 In Multiplication
Sep 08, 2025
-
Gunpowder Empires Ap World History
Sep 08, 2025
-
Power Dissipated By Resistor Formula
Sep 08, 2025
-
Molecular Mass Of Aluminum Oxide
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.