What Is 80 Of 15
scising
Sep 23, 2025 · 5 min read
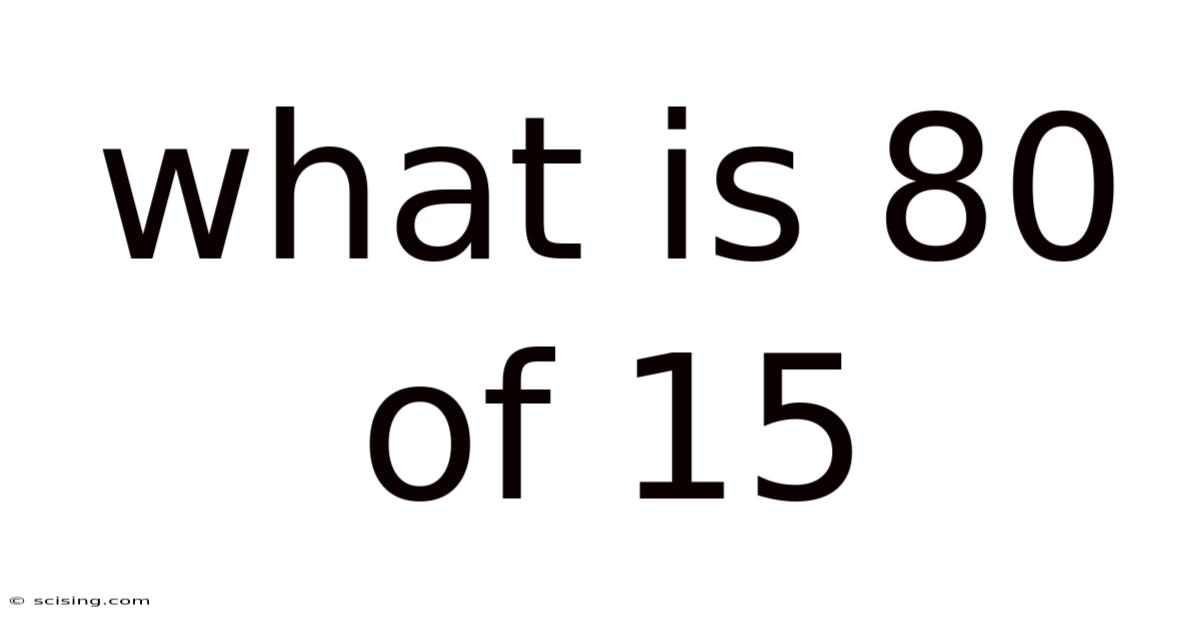
Table of Contents
What is 80% of 15? A Deep Dive into Percentages and Their Applications
Finding 80% of 15 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages opens doors to a wide range of applications in various fields. This article will not only provide the answer but also delve into the methods for calculating percentages, explore different approaches, and discuss real-world examples where this type of calculation proves invaluable. By the end, you'll not only know what 80% of 15 is but also possess a solid understanding of percentage calculations and their practical significance.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." We use the symbol "%" to represent percentages. Therefore, 80% can be written as 80/100, or its simplified fraction, 4/5. This represents 80 parts out of a total of 100 parts. Understanding this fundamental concept is crucial for any percentage calculation.
Method 1: Using Decimal Conversion
The most straightforward method for calculating 80% of 15 involves converting the percentage to a decimal. To do this, we divide the percentage by 100.
-
Step 1: Convert the percentage to a decimal: 80% / 100 = 0.80
-
Step 2: Multiply the decimal by the number: 0.80 * 15 = 12
Therefore, 80% of 15 is 12.
Method 2: Using Fractions
As mentioned earlier, 80% can also be expressed as the fraction 4/5. This provides an alternative method for calculation:
-
Step 1: Express the percentage as a fraction: 80% = 80/100 = 4/5
-
Step 2: Multiply the fraction by the number: (4/5) * 15
-
Step 3: Simplify the calculation: (4 * 15) / 5 = 60 / 5 = 12
Again, the result is 12. This method highlights the interchangeable nature of percentages, decimals, and fractions.
Method 3: Proportion Method
The proportion method offers a more visual approach to understanding percentage calculations. We can set up a proportion:
-
Step 1: Set up the proportion: 80/100 = x/15 (where 'x' represents the unknown value we're trying to find)
-
Step 2: Cross-multiply: 80 * 15 = 100 * x
-
Step 3: Solve for x: 1200 = 100x => x = 1200 / 100 = 12
This method demonstrates the relationship between the percentage and the whole number.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a crucial skill with numerous real-world applications across various fields:
-
Finance: Calculating interest on loans, savings accounts, or investments. Determining discounts on purchases, calculating taxes, understanding profit margins, and analyzing financial statements all rely heavily on percentage calculations. For example, if a store offers an 80% discount on an item originally priced at $15, the discounted price would be $15 - $12 = $3.
-
Science: Expressing experimental results, analyzing data, and representing proportions in scientific studies. For instance, a scientist might report that 80% of a sample exhibited a certain characteristic.
-
Statistics: Calculating percentages is fundamental to interpreting statistical data, such as in opinion polls, surveys, or demographic studies. Understanding percentages allows us to draw meaningful conclusions from large datasets.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, determining the percentage of completion of a task, or figuring out the portion of a recipe are all common scenarios where percentage calculations are essential.
Further Exploration: Beyond the Basics
While calculating 80% of 15 provides a foundation, expanding your understanding of percentages allows you to tackle more complex problems. Here are some areas to explore further:
-
Calculating percentage increase or decrease: This involves determining the percentage change between two values. For example, if a price increases from $10 to $15, the percentage increase is calculated as: [(15-10)/10] * 100% = 50%.
-
Finding the original value: If you know the percentage and the resulting value, you can work backward to determine the original value. For instance, if 80% of a number is 12, the original number is 12 / 0.80 = 15.
-
Compound percentages: These involve applying a percentage repeatedly over time, commonly seen in compound interest calculations.
-
Working with more than one percentage: Problems involving multiple percentages, such as successive discounts, require a step-by-step approach or a combination of the methods discussed earlier.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
- A: The decimal conversion method is generally the most straightforward for simple calculations.
-
Q: How do I calculate a percentage of a number mentally?
- A: Mental calculations often involve simplifying the percentage. For example, 80% is easily halved to 40%, then halved again to 20%, providing a stepwise approach to finding the answer.
-
Q: Are there any online calculators or tools available for percentage calculations?
- A: Numerous online percentage calculators are readily available; these can be helpful for quick calculations or complex scenarios.
-
Q: What if I need to calculate a percentage of a number that is not a whole number?
- A: The methods outlined above work equally well with decimals. Simply multiply the decimal form of the percentage by the decimal number.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key. Try working through various percentage problems of increasing complexity, and utilize different methods to solidify your understanding.
Conclusion: Mastering the Art of Percentage Calculation
Knowing how to calculate 80% of 15, and understanding the broader concept of percentage calculation, is an invaluable skill applicable across various aspects of life. By mastering these techniques, you equip yourself with a tool for making informed decisions, analyzing data effectively, and solving problems with confidence. Remember that understanding the fundamental principles, practicing different methods, and exploring real-world applications are crucial steps towards becoming proficient in percentage calculations. The seemingly simple calculation of finding 80% of 15 opens a door to a much wider world of mathematical understanding and practical application. This knowledge is more than just a mathematical skill; it's a powerful tool for navigating the complexities of the world around us.
Latest Posts
Latest Posts
-
How Much Is 600 Milliliters
Sep 23, 2025
-
Barar And Abdollahi Cell Model
Sep 23, 2025
-
How Much Is 3 L
Sep 23, 2025
-
Salir In The Present Tense
Sep 23, 2025
-
4 000 Pounds To Tons
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.