What Is 45 Of 40
scising
Sep 20, 2025 · 5 min read
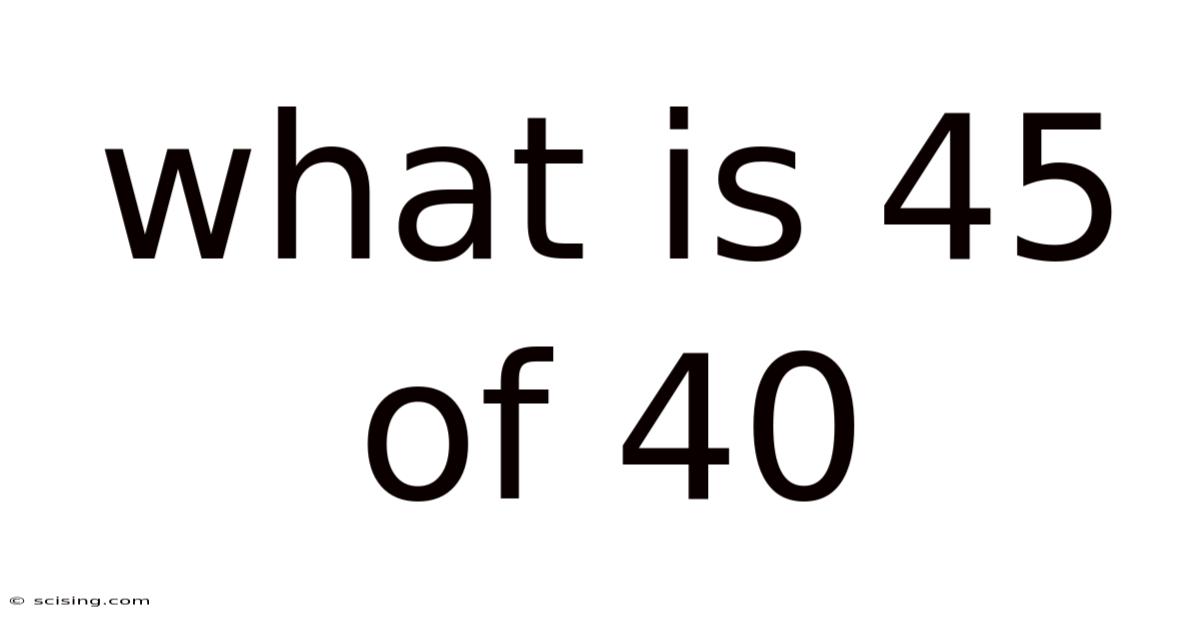
Table of Contents
What is 45% of 40? A Deep Dive into Percentages and Their Applications
This article will comprehensively explore the question, "What is 45% of 40?", going beyond a simple numerical answer to delve into the underlying principles of percentage calculations, their real-world applications, and common misconceptions. Understanding percentages is a fundamental skill applicable across various fields, from finance and business to science and everyday life. We'll break down the calculation step-by-step, offer alternative approaches, and explore the broader context of percentage applications.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (from the Latin "per centum"). Therefore, 45% means 45 out of 100, or 45/100. This fractional representation is key to understanding how percentage calculations work.
Calculating 45% of 40: Step-by-Step
The most straightforward way to calculate 45% of 40 is to follow these steps:
-
Convert the percentage to a decimal: Divide the percentage by 100. 45% ÷ 100 = 0.45
-
Multiply the decimal by the number: Multiply the decimal obtained in step 1 by the number you want to find the percentage of (40 in this case). 0.45 x 40 = 18
Therefore, 45% of 40 is 18.
Alternative Methods: Different Approaches, Same Result
While the above method is the most common, there are other ways to calculate percentages, each offering different perspectives and advantages depending on the context:
-
Using Fractions: We know that 45% is equivalent to 45/100. We can rewrite the problem as (45/100) x 40. This simplifies to (9/20) x 40, which further simplifies to 9 x 2 = 18. This method emphasizes the fractional nature of percentages.
-
Proportion Method: Set up a proportion: 45/100 = x/40. Cross-multiply to solve for x: 100x = 45 x 40. Solving for x gives x = (45 x 40) / 100 = 18. This method is useful for understanding the proportional relationship between percentages and quantities.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 45%, then the multiplication sign, then 40, and press the equals sign (=). The calculator will directly provide the answer: 18. This method is efficient for quick calculations.
Real-World Applications: Where Percentages Matter
Percentages are ubiquitous, appearing in numerous contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investment all rely heavily on percentage calculations. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase necessitates a firm grasp of percentages.
-
Business: Analyzing market share, sales growth, cost reductions, and various key performance indicators (KPIs) often involves percentage calculations. Businesses use percentages to track progress, identify trends, and make informed decisions.
-
Science: Percentages are used extensively in expressing concentrations (e.g., a 10% saline solution), statistical analysis (e.g., confidence intervals), and experimental results (e.g., percentage error). Accurate percentage calculations are crucial for scientific rigor.
-
Everyday Life: We encounter percentages daily – tipping in restaurants (e.g., a 15% tip), calculating sales tax, understanding nutritional information on food labels (e.g., percentage of daily value), and interpreting statistical data in news reports.
Common Misconceptions about Percentages
While seemingly straightforward, percentages can sometimes lead to confusion. Here are some common misconceptions:
-
Adding Percentages Directly: You cannot simply add percentages together unless they are applied to the same base. For example, a 10% increase followed by a 10% decrease does not result in a net change of 0%. The second 10% decrease is calculated on the new, increased value.
-
Misunderstanding Percentage Changes: A percentage increase or decrease is always relative to the original value. A 10% increase from 100 is 110, but a 10% decrease from 110 is only 99, not 100.
-
Ignoring the Base: The base value (the number you are calculating the percentage of) is critical. 45% of 40 is different from 45% of 100 or 45% of any other number.
Advanced Percentage Calculations: Extending Your Knowledge
Beyond the basic calculation of "45% of 40," understanding percentages involves more complex scenarios:
-
Calculating Percentage Increase/Decrease: Determining the percentage change between two values involves finding the difference between the two values, dividing that difference by the original value, and multiplying by 100%.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value using algebraic equations.
-
Compounding Percentages: When percentages are applied repeatedly (e.g., compound interest), the calculations become more intricate, requiring an understanding of exponential growth.
-
Weighted Averages and Percentages: In situations with different weights or proportions, weighted averages are used, where each value contributes differently to the overall percentage.
Frequently Asked Questions (FAQ)
-
What if I need to calculate a different percentage of 40? The same methods apply. Simply replace 45% with the desired percentage and follow the steps outlined above.
-
How can I improve my percentage calculation skills? Practice is key. Try solving various percentage problems, using different methods, and checking your answers. Online resources and practice worksheets can be helpful.
-
Are there any online tools to help calculate percentages? Yes, numerous online percentage calculators are available that can instantly compute percentages for you. However, understanding the underlying principles remains crucial.
-
What are some real-world examples of percentage problems I might encounter? Calculating sales tax, discounts at stores, figuring out tips at restaurants, or interpreting statistical data in the news are all common examples.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "What is 45% of 40?" opens a door to a vast world of mathematical applications. Understanding percentages is a fundamental skill crucial for success in various aspects of life. By mastering the different methods of calculating percentages and appreciating their diverse applications, you equip yourself with a powerful tool for navigating the quantitative challenges we encounter daily, whether in personal finances, professional pursuits, or simply understanding the world around us. Remember to practice regularly, explore different approaches, and avoid common misconceptions to solidify your understanding and enhance your problem-solving abilities. The seemingly simple calculation of 45% of 40 serves as a springboard to a deeper understanding of percentages and their vital role in our lives.
Latest Posts
Latest Posts
-
Book A Farewell To Arms
Sep 20, 2025
-
Joan Of Arc Fun Facts
Sep 20, 2025
-
William The Conqueror Family Tree
Sep 20, 2025
-
Speaking Outline For Informative Speech
Sep 20, 2025
-
Tallest Bridge In The China
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 45 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.