What Is 32 Of 50
scising
Sep 13, 2025 · 5 min read
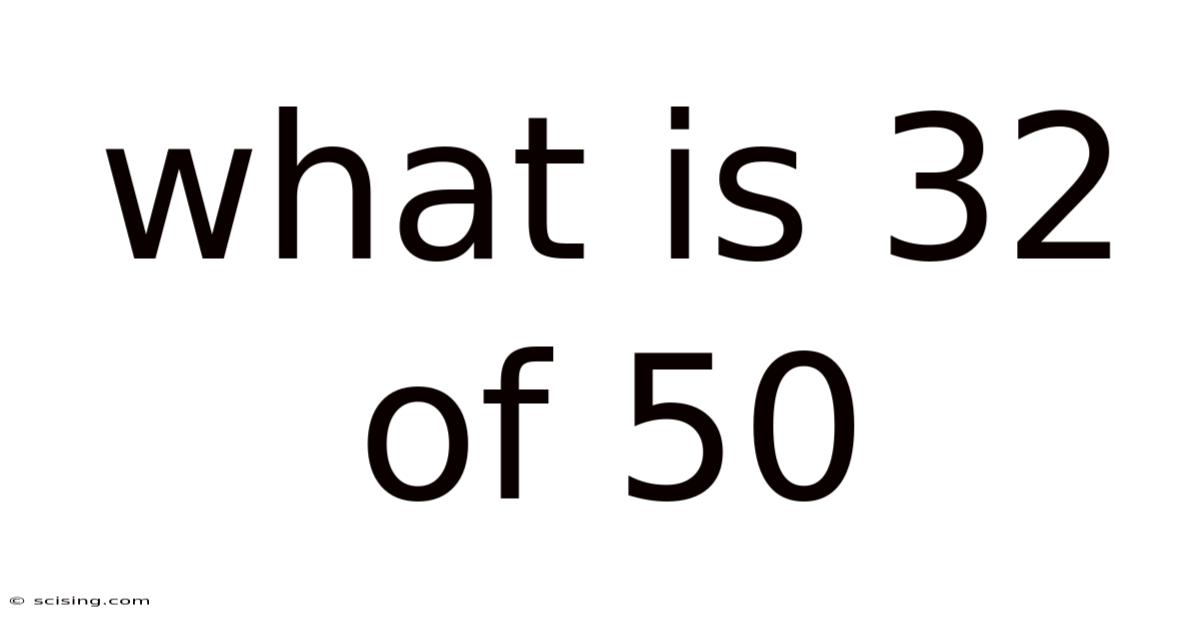
Table of Contents
What is 32 out of 50? Understanding Fractions, Percentages, and Ratios
"What is 32 out of 50?" This seemingly simple question opens a door to a world of mathematical concepts, including fractions, percentages, and ratios. Understanding how to solve this, and similar problems, is fundamental to various aspects of life, from calculating grades to understanding financial data. This comprehensive guide will not only answer the question but also equip you with the skills and knowledge to tackle similar problems with confidence.
Understanding the Core Concepts
Before diving into the calculation, let's clarify the three key mathematical concepts involved: fractions, percentages, and ratios.
-
Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). In our case, "32 out of 50" is represented as the fraction 32/50. The numerator (32) represents the part, and the denominator (50) represents the whole.
-
Percentages: A percentage is a fraction expressed as a number out of 100. It's often denoted with the symbol "%". Percentages are useful for comparing proportions and making comparisons easier to understand. Converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100.
-
Ratios: A ratio compares two or more quantities. It can be expressed in different ways: using the colon (e.g., 32:50), using the word "to" (e.g., 32 to 50), or as a fraction (e.g., 32/50). In this context, the ratio shows the relationship between the part (32) and the whole (50).
Calculating 32 out of 50: Step-by-Step
Now, let's tackle the central question: what is 32 out of 50? We can approach this using different methods:
1. Expressing it as a Fraction:
The most straightforward representation is the fraction 32/50. This accurately reflects the part (32) out of the whole (50). However, this fraction can be simplified.
Simplifying the Fraction:
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 32 and 50 is 2. Divide both the numerator and denominator by the GCD:
32 ÷ 2 = 16 50 ÷ 2 = 25
Therefore, the simplified fraction is 16/25. This is an equivalent fraction to 32/50, meaning they represent the same proportion.
2. Converting to a Percentage:
To convert the fraction 32/50 (or its simplified form 16/25) to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by a number that will result in a denominator of 100.
Since 25 x 4 = 100, we multiply both the numerator and denominator of 16/25 by 4:
16 x 4 = 64 25 x 4 = 100
This gives us the equivalent fraction 64/100, which is equal to 64%. Therefore, 32 out of 50 is 64%.
Alternatively, you can use the following formula:
Percentage = (Part / Whole) x 100
In this case:
Percentage = (32 / 50) x 100 = 0.64 x 100 = 64%
3. Expressing it as a Decimal:
To express 32 out of 50 as a decimal, simply divide the numerator (32) by the denominator (50):
32 ÷ 50 = 0.64
This decimal, 0.64, is equivalent to 64%.
Real-World Applications
Understanding how to calculate proportions, as demonstrated with "32 out of 50," has numerous practical applications:
-
Calculating Grades: If you answered 32 questions correctly out of 50 on a test, your score would be 64%.
-
Financial Analysis: In finance, understanding ratios and percentages is crucial for analyzing financial statements, calculating returns on investments, and assessing risk.
-
Data Interpretation: Many statistical analyses involve calculating proportions and percentages from data sets. Understanding these concepts is crucial for interpreting and making sense of the data.
-
Recipe Scaling: If a recipe calls for 32 grams of flour for 50 cookies, you can use this proportion to scale the recipe up or down.
-
Probability: In probability calculations, you often express the likelihood of an event as a fraction or percentage.
Further Exploration: Working with Different Proportions
The methods outlined above can be applied to any similar problem. For instance, let's consider a slightly different scenario:
Example: What is 18 out of 30?
-
Fraction: 18/30. Simplified, this is 3/5.
-
Percentage: To convert 3/5 to a percentage, multiply both numerator and denominator by 20 (since 5 x 20 = 100): (3 x 20) / (5 x 20) = 60/100 = 60%. Alternatively, (18/30) x 100 = 60%.
-
Decimal: 18 ÷ 30 = 0.6
This example reinforces the versatility of the methods described earlier. You can adapt these techniques to calculate proportions in various contexts.
Frequently Asked Questions (FAQ)
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and compare. A simplified fraction represents the same proportion as the original fraction but in its most concise form.
Q: Can I use a calculator for these calculations?
A: Yes, calculators can significantly speed up the process of converting fractions to percentages or decimals.
Q: What if I have a more complex fraction?
A: The same principles apply. You can simplify the fraction and then convert it to a percentage or decimal using the methods described above. If the fraction has a very large denominator, a calculator will be particularly helpful.
Q: Are there any online tools that can help with these calculations?
A: Yes, many online calculators are available to perform fraction, percentage, and ratio calculations.
Conclusion
This article has thoroughly explored the question "What is 32 out of 50?" demonstrating how to represent this proportion as a fraction, percentage, and decimal. By understanding fractions, percentages, and ratios, you gain essential skills applicable to various aspects of life. Remember that the key lies in understanding the underlying concepts and applying the appropriate methods to solve the problem at hand. Practice makes perfect, so try working through different examples to strengthen your understanding and build confidence in your ability to handle similar calculations. Mastering these concepts will enhance your mathematical skills and improve your problem-solving abilities across various disciplines.
Latest Posts
Latest Posts
-
Quadratic Function Minimum And Maximum
Sep 13, 2025
-
What Is 15 In Percentage
Sep 13, 2025
-
Forms Of Studiere In German
Sep 13, 2025
-
Is 11 A Rational Number
Sep 13, 2025
-
Differences Between Mesopotamia And Egypt
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 32 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.