What Is 25 Of 8
scising
Sep 19, 2025 · 5 min read
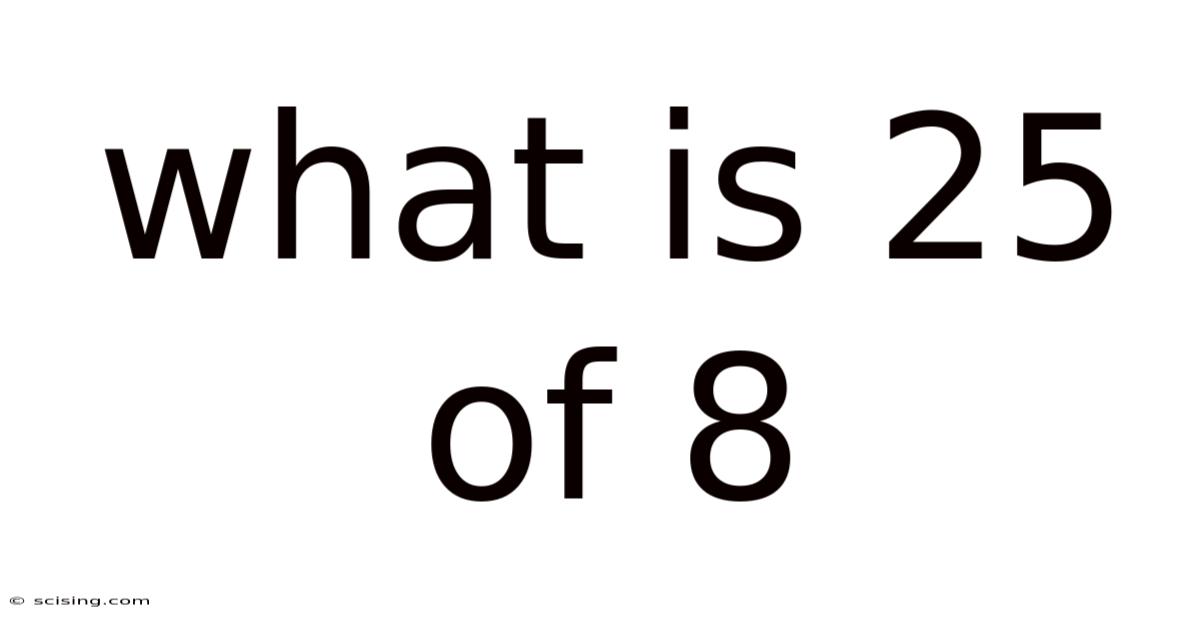
Table of Contents
What is 25% of 8? A Deep Dive into Percentages and Their Applications
This article will comprehensively explore the question: "What is 25% of 8?" We'll not only solve this specific problem but also delve into the broader understanding of percentages, their calculation methods, and their wide-ranging applications in various fields. Understanding percentages is a fundamental skill applicable in everyday life, from calculating discounts to understanding financial reports and analyzing statistical data.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 25% literally means 25 out of 100, or 25/100. This fraction can be simplified to 1/4.
Percentages are used extensively to represent proportions, ratios, and rates of change. They provide a standardized way to compare different quantities, making it easier to understand and interpret data. For example, a 10% increase in sales is easily understood and comparable to a 5% increase, regardless of the original sales figures.
Calculating 25% of 8: Three Different Methods
There are several ways to calculate 25% of 8. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As mentioned earlier, 25% is equivalent to the fraction 1/4. To find 25% of 8, we simply multiply 8 by 1/4:
8 x (1/4) = 8/4 = 2
Therefore, 25% of 8 is 2.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100:
25% ÷ 100 = 0.25
Now, multiply this decimal by 8:
0.25 x 8 = 2
Again, we arrive at the answer: 25% of 8 is 2.
Method 3: Using Proportions
This method involves setting up a proportion. We know that 25% is 25 out of 100. We can set up the following proportion:
25/100 = x/8
To solve for x (which represents 25% of 8), we cross-multiply:
25 * 8 = 100 * x
200 = 100x
x = 200/100 = 2
Once more, we find that 25% of 8 is 2.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a crucial skill with numerous real-world applications:
-
Shopping and Discounts: Calculating discounts on sale items is a common application. If a shirt is priced at $20 and is on sale for 25% off, you can quickly determine the discount amount ($5) and the final price ($15).
-
Finance and Investments: Understanding interest rates, returns on investments, and loan calculations all rely heavily on percentage calculations. For example, calculating compound interest requires repeated percentage calculations.
-
Taxes and Tax Rates: Tax calculations involve determining a percentage of income or the value of goods and services. Understanding tax brackets and calculating tax owed necessitates proficiency in percentage calculations.
-
Statistics and Data Analysis: Percentages are essential for presenting and interpreting statistical data. For example, expressing survey results as percentages allows for easy comparison and understanding of trends.
-
Science and Engineering: Percentage calculations are used in many scientific and engineering applications, such as calculating efficiency, error rates, and concentrations of solutions.
-
Everyday Life: From calculating tips in restaurants to understanding nutritional information on food labels, percentages are interwoven into our daily routines.
Expanding the Understanding: Beyond 25% of 8
While we've focused on calculating 25% of 8, let's broaden our scope. Consider the following related concepts:
-
Calculating x% of y: The general formula for calculating x% of y is: (x/100) * y. This formula allows you to calculate the percentage of any number.
-
Finding the Percentage One Number Represents of Another: Suppose you sold 2 items out of 8. To find the percentage of items sold, you'd divide the number sold (2) by the total number (8) and multiply by 100: (2/8) * 100 = 25%.
-
Percentage Increase and Decrease: These calculations are crucial for understanding growth or decline in various aspects of life. A percentage increase is calculated as [(New Value - Old Value) / Old Value] * 100, while a percentage decrease is calculated as [(Old Value - New Value) / Old Value] * 100.
-
Working Backwards from a Percentage: Sometimes you know the percentage and the resulting value, and you need to find the original value. For example, if 25% of a number is 2, you can set up an equation: 0.25x = 2. Solving for x, we find x = 8.
Frequently Asked Questions (FAQs)
Q: What is the easiest method to calculate percentages?
A: The easiest method often depends on personal preference and the specific numbers involved. Using the fraction equivalent can be simple for common percentages like 25%, 50%, and 75%. Converting to decimals is generally straightforward for most percentages. The proportion method is helpful for understanding the underlying concept and can be applied to various percentage problems.
Q: Are there any online calculators for percentages?
A: Yes, many online calculators are available that can quickly compute percentages. These are useful for checking your calculations or for complex percentage problems. However, understanding the underlying concepts remains crucial for problem-solving and real-world application.
Q: How can I improve my skills in calculating percentages?
A: Practice is key! Start with simple problems and gradually increase the complexity. Use different methods to solve the same problem to reinforce your understanding. Look for opportunities to apply percentage calculations in real-life situations. Online resources and educational materials can provide further support and practice exercises.
Q: What if the percentage is not a whole number, such as 12.5%?
A: The same methods apply. You can convert 12.5% to a decimal (0.125) or a fraction (1/8) and proceed with the calculations as described earlier.
Conclusion
Calculating 25% of 8, as we've demonstrated, is a straightforward process with multiple approaches. However, the significance of understanding percentages extends far beyond this single calculation. Percentages are an integral part of numerous aspects of life, from personal finance to professional fields. Mastering percentage calculations equips you with a powerful tool for problem-solving, analysis, and informed decision-making in various contexts. The key is to practice consistently and explore different methods to solidify your understanding and build confidence in applying these skills. The more you engage with percentage calculations, the more intuitive and effortless they will become.
Latest Posts
Latest Posts
-
1 Pint To Fluid Ounces
Sep 19, 2025
-
Use Anecdote In A Sentence
Sep 19, 2025
-
Cades Cove Primitive Baptist Church
Sep 19, 2025
-
La Bourse Ou La Vie
Sep 19, 2025
-
Map Of United States Deserts
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.