What Is 25 Of 100.00
scising
Sep 11, 2025 · 5 min read
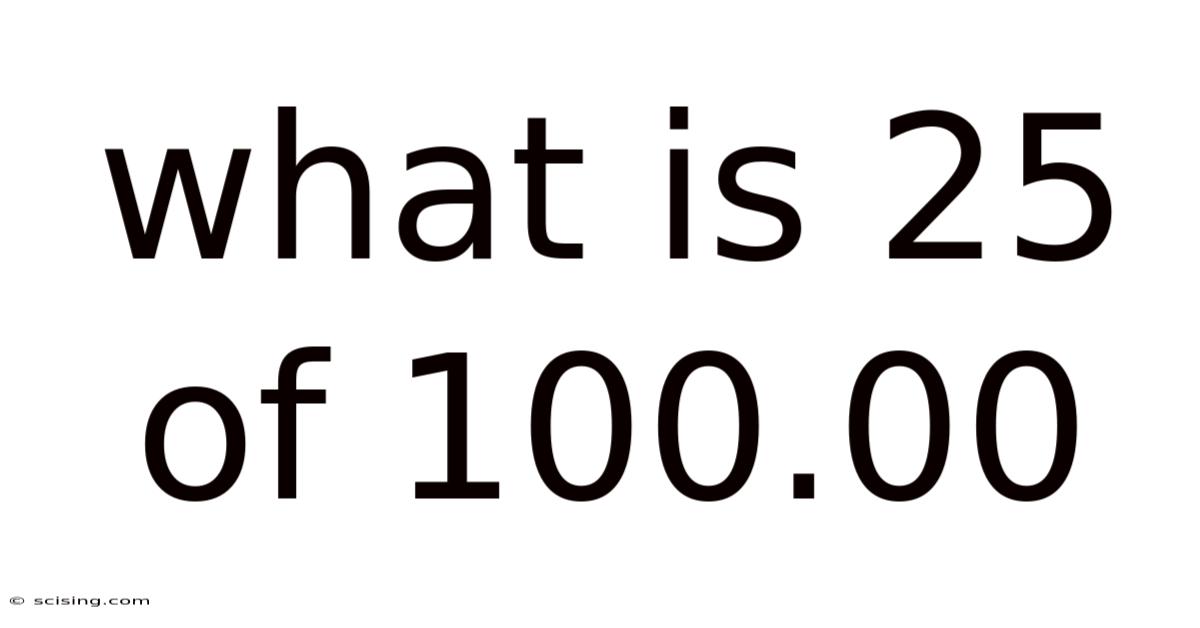
Table of Contents
What is 25 of 100.00? Understanding Percentages and Their Applications
This article delves into the seemingly simple question: "What is 25 of 100.00?" While the answer might appear obvious at first glance, exploring this question unlocks a deeper understanding of percentages, their practical applications, and their significance in various fields. We'll move beyond the basic calculation to explore the underlying mathematical principles and demonstrate how percentage calculations are used in everyday life, from finance and shopping to science and statistics.
Understanding Percentages: A Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, or 25/100. This fundamental concept forms the bedrock of numerous calculations and analyses across diverse disciplines.
Calculating 25 of 100.00: The Simple Approach
The simplest way to determine 25 of 100.00 is to recognize that 25% of 100.00 is equivalent to multiplying 100.00 by 0.25 (the decimal equivalent of 25%).
100.00 x 0.25 = 25.00
Therefore, 25 of 100.00 is 25.00.
This calculation is straightforward and easily performed using a calculator or even mental arithmetic. However, understanding the underlying principles provides a more robust grasp of percentage calculations.
Beyond the Basic Calculation: Exploring Percentage Methods
While the direct multiplication method is efficient, let's explore alternative approaches to solve this problem, enhancing our understanding of percentage calculations:
-
Fraction Method: We can express 25% as a fraction: 25/100. Then, we can multiply this fraction by 100.00:
(25/100) x 100.00 = 25.00
This method highlights the direct relationship between fractions and percentages.
-
Ratio Method: We can set up a proportion:
25/100 = x/100.00
Solving for x, we get:
x = (25/100) x 100.00 = 25.00
This approach demonstrates the proportional relationship between the percentage and the whole value.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Let's examine some examples:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentage calculations. Understanding compound interest, for instance, requires a thorough grasp of percentage growth over time. Determining tax amounts, discounts, and profit margins also involve percentage computations. For example, a 10% discount on a $100 item means a reduction of $10 (10% of $100).
-
Shopping: Sales, discounts, and value-added taxes (VAT) are all expressed as percentages. Being able to quickly calculate these percentages allows consumers to make informed purchasing decisions. Comparing prices and identifying the best deals often requires deft manipulation of percentages.
-
Science and Statistics: Percentages are extensively used in scientific research and statistical analysis. Data representation, error analysis, and hypothesis testing often involve calculating and interpreting percentages. For example, expressing experimental results as percentages helps in comparing different experimental groups or conditions. Statistical significance is often determined based on percentage changes or differences.
-
Everyday Life: Percentages are pervasive in daily life. Understanding tip calculations in restaurants, figuring out the percentage of ingredients in recipes, or calculating the percentage of completion of a task all involve percentage calculations. Even determining the percentage of votes a candidate receives in an election utilizes percentage calculations.
Advanced Percentage Calculations: Beyond the Basics
While the example of 25 of 100.00 is relatively simple, percentage calculations can become more complex. Consider these scenarios:
-
Calculating Percentage Increase or Decrease: Determining the percentage change between two values requires understanding the concept of percentage difference. For example, if a stock price increases from $50 to $60, the percentage increase is calculated as follows:
((60-50)/50) x 100% = 20%
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, you can work backward to determine the original value. For example, if a price of $75 represents a 25% increase from the original price, the original price can be calculated as:
$75 / 1.25 = $60
-
Calculating Multiple Percentages: Sometimes, we need to apply multiple percentages successively. For instance, calculating the final price after a 10% discount followed by a 5% sales tax requires sequential percentage calculations.
-
Percentage of a Percentage: This involves finding a percentage of a percentage, which requires careful calculation. For instance, if 20% of a population represents 10% of the total workforce, it's important to differentiate between these two different percentages and their relation to the whole.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method is often direct multiplication. Convert the percentage to a decimal (divide by 100) and multiply it by the number you're finding the percentage of.
Q: How can I improve my percentage calculation skills?
A: Practice is key. Work through various examples, starting with simple calculations and gradually progressing to more complex ones. Understanding the underlying mathematical principles is also vital.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online calculators and tools are readily available to assist with various percentage calculations. These tools can be helpful for quick calculations and verification of results.
Q: Why are percentages important?
A: Percentages provide a standardized and readily understandable way to represent proportions and ratios. Their use simplifies comparisons and analyses across different datasets and contexts. They are essential tools for making informed decisions in various fields.
Q: What are some common mistakes to avoid when calculating percentages?
A: Some common mistakes include incorrect decimal conversion, misinterpreting percentage increase/decrease, and failing to account for multiple percentage applications. Careful attention to detail and a solid understanding of the underlying concepts are crucial to avoid these errors.
Conclusion: Mastering the Power of Percentages
Understanding "what is 25 of 100.00" extends far beyond a simple arithmetic calculation. It opens the door to a deeper appreciation of percentages, their versatility, and their pervasive role in various aspects of life. By mastering the principles of percentage calculations, we equip ourselves with valuable tools for navigating the quantitative aspects of the world around us – from managing personal finances to comprehending complex scientific data. The seemingly simple calculation of 25% of 100.00 serves as a springboard to unlocking a wealth of quantitative literacy, empowering us to approach numerical challenges with greater confidence and skill.
Latest Posts
Latest Posts
-
State With The Longest Name
Sep 11, 2025
-
St Nicholas Serbian Orthodox Church
Sep 11, 2025
-
Examples Of K Selected Species
Sep 11, 2025
-
What Is Physical Features Mean
Sep 11, 2025
-
What Is 80 Of 70
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 100.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.