What Is 24 Of 60
scising
Sep 13, 2025 · 5 min read
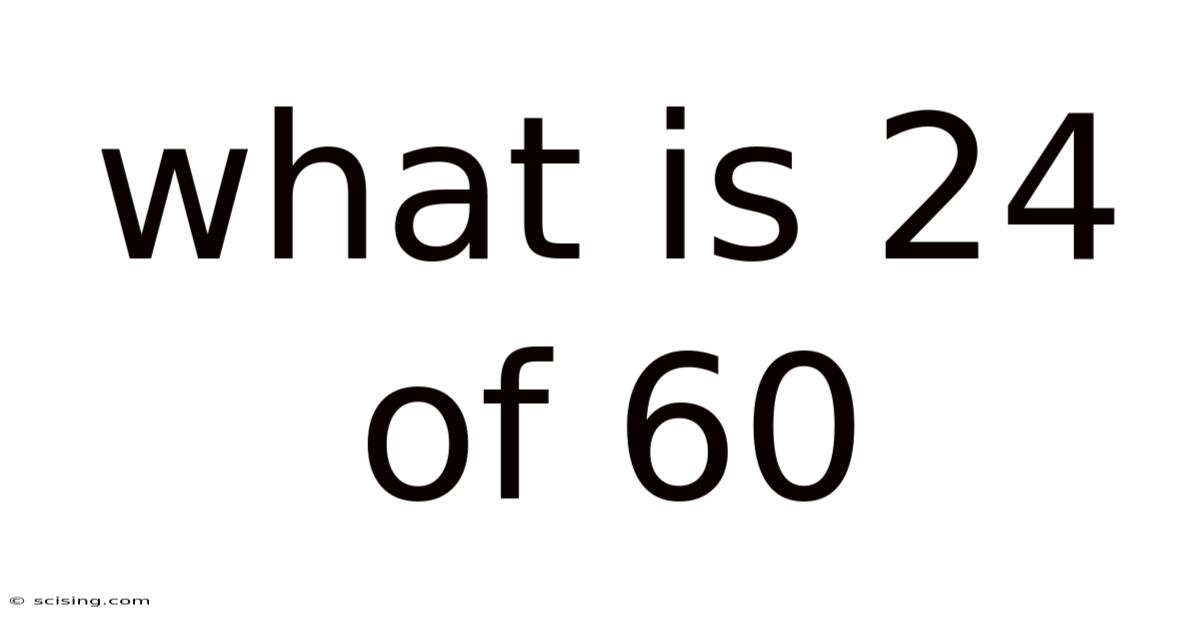
Table of Contents
What is 24 of 60? Unveiling the World of Fractions, Percentages, and Ratios
What is 24 out of 60? This seemingly simple question opens a door to a world of mathematical concepts vital for everyday life, from calculating discounts to understanding statistics. This article will explore various ways to interpret and solve this problem, delving into the fundamental principles of fractions, percentages, and ratios, providing a comprehensive understanding for learners of all levels.
Introduction: Understanding the Core Concepts
The phrase "24 of 60" represents a part-to-whole relationship. It signifies that 24 is a portion of a larger whole, 60. We can express this relationship in several ways: as a fraction, a percentage, or a ratio. Each representation offers a unique perspective and has practical applications. Understanding these different representations is crucial for effective problem-solving and interpreting data in various contexts. We'll examine each representation in detail, revealing the mathematical processes involved and highlighting their real-world significance.
1. Expressing "24 of 60" as a Fraction
A fraction represents a part of a whole. In this case, 24 is the part and 60 is the whole. Therefore, we can express "24 of 60" as the fraction 24/60.
-
Simplifying the Fraction: Fractions are often simplified to their lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (24) and the denominator (60) and dividing both by it. The GCD of 24 and 60 is 12.
24 ÷ 12 = 2 60 ÷ 12 = 5
Therefore, the simplified fraction is 2/5. This means that 24 out of 60 is equivalent to 2 parts out of every 5 parts.
-
Understanding the Significance of Simplification: Simplifying fractions makes them easier to understand and compare. The simplified fraction 2/5 provides a more concise and manageable representation of the relationship between 24 and 60.
2. Converting "24 of 60" to a Percentage
A percentage represents a fraction out of 100. To convert the fraction 24/60 (or its simplified form, 2/5) to a percentage, we need to find an equivalent fraction with a denominator of 100.
-
Method 1: Using the Simplified Fraction:
We can set up a proportion:
2/5 = x/100
Cross-multiplying, we get:
5x = 200
Dividing both sides by 5, we find:
x = 40
Therefore, 24/60 is equal to 40%.
-
Method 2: Using the Original Fraction:
We can directly convert 24/60 to a percentage by dividing 24 by 60 and multiplying the result by 100:
(24/60) * 100 = 40%
-
Interpreting the Percentage: 40% signifies that 24 represents 40 out of every 100 parts of the whole (60). This representation is widely used in various applications, including calculating discounts, expressing probabilities, and representing data in graphs and charts.
3. Expressing "24 of 60" as a Ratio
A ratio compares two quantities. In this case, we can express the relationship between 24 and 60 as the ratio 24:60. Like fractions, ratios can be simplified by dividing both parts by their GCD (12).
24 ÷ 12 = 2 60 ÷ 12 = 5
The simplified ratio is 2:5. This means that for every 2 parts of one quantity, there are 5 parts of the other.
- Applications of Ratios: Ratios are frequently used in various fields, including cooking (e.g., mixing ingredients), scaling drawings, and comparing different quantities. The simplified ratio 2:5 provides a concise and easily understandable comparison between 24 and 60.
4. Real-World Applications and Examples
Understanding fractions, percentages, and ratios is crucial for navigating various aspects of daily life. Here are some examples illustrating the practical applications of understanding "24 of 60":
- Test Scores: If you answered 24 questions correctly out of 60 on a test, your score is 40%.
- Sales and Discounts: A store offers a 40% discount on an item. If the original price is $60, the discount amount is $24.
- Surveys and Statistics: If 24 out of 60 respondents answered "yes" to a survey question, 40% of respondents answered "yes".
- Ingredient Ratios: A recipe calls for a 2:5 ratio of sugar to flour. If you use 24 units of sugar, you should use 60 units of flour.
5. Expanding the Understanding: Further Mathematical Concepts
The simple question "What is 24 of 60?" opens doors to several interconnected mathematical concepts:
- Proportions: We used proportions to convert the fraction to a percentage. Understanding proportions is fundamental for solving problems involving similar triangles, scaling, and other mathematical applications.
- Decimals: The fraction 2/5 can be expressed as a decimal: 0.4. Decimals provide another way to represent parts of a whole, often used in financial calculations and scientific measurements.
- Probability: The fraction 2/5 or 40% can represent the probability of a certain event occurring. Understanding probability is crucial in various fields, including statistics, risk assessment, and game theory.
6. Frequently Asked Questions (FAQs)
-
Q: What is the simplest way to calculate the percentage? A: The easiest way is to divide the part by the whole and then multiply by 100: (24/60) * 100 = 40%.
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in further calculations. It provides a more concise representation of the relationship between the numerator and denominator.
-
Q: Are fractions, percentages, and ratios always interchangeable? A: Yes, they all represent the same part-to-whole relationship, but each offers a different way of expressing it. The choice of which to use often depends on the context and the desired level of precision.
-
Q: Can I use a calculator to solve this problem? A: Absolutely! A calculator can simplify the calculations involved in converting fractions to percentages or decimals. However, understanding the underlying mathematical concepts is crucial for applying these methods effectively in different situations.
7. Conclusion: Mastering the Fundamentals
The question "What is 24 of 60?" might seem straightforward, but it serves as a gateway to understanding fundamental mathematical concepts: fractions, percentages, and ratios. Mastering these concepts is not just about performing calculations; it's about developing a deeper understanding of how to represent and interpret quantitative information in the real world. This ability is vital for making informed decisions, analyzing data, and successfully navigating various aspects of life, from personal finance to scientific research. The ability to effortlessly translate between fractions, percentages, and ratios demonstrates a strong foundation in numerical literacy, a skillset invaluable in numerous fields. By understanding the underlying principles, you empower yourself to tackle more complex mathematical problems with confidence and clarity.
Latest Posts
Latest Posts
-
Analogy For A Cell Membrane
Sep 13, 2025
-
What Are Spanish Indefinite Articles
Sep 13, 2025
-
Is A 3 3 Gpa Good
Sep 13, 2025
-
How To Subtract A Negative
Sep 13, 2025
-
Is A Snail An Invertebrate
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 24 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.