What Is 20 Of 32
scising
Sep 10, 2025 · 5 min read
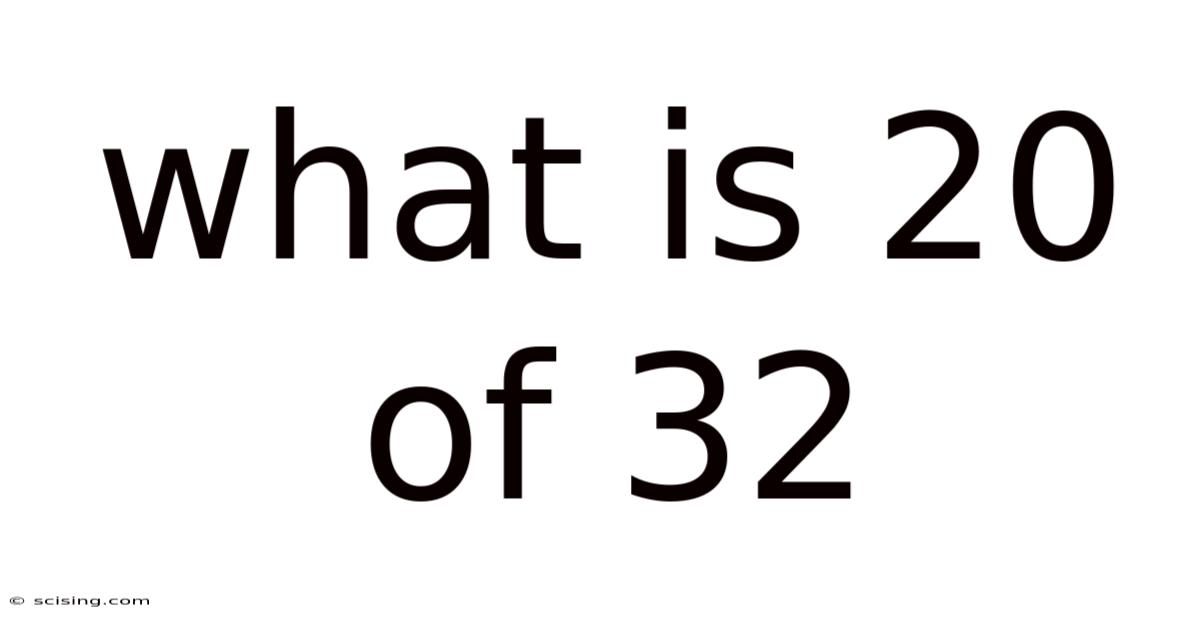
Table of Contents
What is 20 of 32? Unveiling the World of Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 32?", opens a door to a fascinating world of mathematical concepts that underpin our daily lives. Understanding how to solve this problem involves more than just a simple calculation; it's about grasping the core principles of fractions, percentages, and ratios. This article will not only provide the answer but delve deep into the underlying mathematical concepts, exploring different ways to approach the problem and offering practical applications. We'll explore various methods, ensuring you leave with a comprehensive understanding, regardless of your prior mathematical experience.
Understanding the Problem: Fractions, Percentages, and Ratios
The question "What is 20 of 32?" can be interpreted in several ways, all related to the fundamental concepts of fractions, percentages, and ratios. Let's break down each interpretation:
-
Fraction: The phrase "20 of 32" directly translates to the fraction 20/32. This represents 20 parts out of a total of 32 parts. Understanding fractions is crucial in numerous fields, from cooking and construction to finance and programming.
-
Percentage: We can express the fraction 20/32 as a percentage, representing the proportion of 20 relative to 32 as a value out of 100. Percentages are widely used to express proportions, particularly in financial reports, statistics, and everyday contexts like sales discounts.
-
Ratio: The relationship between 20 and 32 can also be expressed as a ratio, 20:32. Ratios are used to compare the relative sizes of two or more quantities. They are essential in various areas, including scaling recipes, mapmaking, and understanding proportions in scientific experiments.
Calculating 20 of 32: Step-by-Step Solutions
Let's now explore different ways to calculate "20 of 32," covering various mathematical approaches.
1. Simplifying the Fraction:
The simplest approach is to simplify the fraction 20/32. We look for the greatest common divisor (GCD) of 20 and 32, which is 4. Dividing both the numerator and denominator by 4, we get:
20/32 = (20 ÷ 4) / (32 ÷ 4) = 5/8
Therefore, 20 out of 32 is equivalent to 5/8. This simplified fraction is easier to understand and use in further calculations.
2. Converting to a Percentage:
To convert the fraction 5/8 to a percentage, we divide the numerator (5) by the denominator (8) and multiply the result by 100:
(5/8) * 100 = 0.625 * 100 = 62.5%
Therefore, 20 out of 32 is equal to 62.5%.
3. Decimal Representation:
We can also express the fraction 5/8 as a decimal by performing the division:
5 ÷ 8 = 0.625
This decimal representation is useful for various calculations and comparisons.
4. Using Ratio and Proportion:
The ratio 20:32 can be simplified by dividing both sides by their GCD (4):
20:32 = 5:8
This simplified ratio shows the same proportional relationship as the simplified fraction 5/8.
Deeper Dive into Mathematical Concepts
Let's delve deeper into the mathematical concepts involved to enhance your understanding.
1. Fractions: A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of parts. Fractions can be simplified by finding the GCD of the numerator and denominator and dividing both by it.
2. Percentages: A percentage is a fraction expressed as a number out of 100. To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. Percentages provide a standardized way to compare proportions.
3. Ratios: A ratio compares the relative sizes of two or more quantities. It can be expressed using a colon (e.g., 5:8) or as a fraction (e.g., 5/8). Ratios are essential for understanding proportional relationships.
Practical Applications
Understanding fractions, percentages, and ratios is vital in many real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins.
- Cooking: Scaling recipes up or down, understanding ingredient proportions.
- Construction: Measuring materials, calculating areas and volumes.
- Data Analysis: Interpreting statistical data, presenting proportions in charts and graphs.
- Everyday Life: Sharing items fairly, calculating tips, understanding sale prices.
Frequently Asked Questions (FAQ)
Q1: What if I want to find 20% of 32?
A1: To find 20% of 32, we multiply 32 by 0.20 (which is the decimal equivalent of 20%). 32 * 0.20 = 6.4. This is different from finding "20 of 32," which represents the fraction 20/32.
Q2: How can I quickly simplify fractions?
A2: The easiest method is to find the GCD of the numerator and the denominator. You can do this by listing the factors of each number and finding the largest common factor. Alternatively, you can use the Euclidean algorithm, a more efficient method for larger numbers.
Q3: Are there any online tools to help with fraction simplification and percentage calculations?
A3: Yes, many online calculators are available that can simplify fractions and convert fractions to percentages. These tools can be helpful for quick calculations and checking your work. However, it's crucial to understand the underlying concepts to apply them effectively in various situations.
Conclusion: Mastering the Fundamentals
In conclusion, "What is 20 of 32?" is more than just a simple calculation. It's an opportunity to explore the fundamental concepts of fractions, percentages, and ratios – essential tools for navigating the mathematical world and solving real-world problems. By mastering these concepts and understanding the different methods of calculation, you'll build a strong foundation for more advanced mathematical studies and everyday applications. Remember, the key is to practice regularly and apply these concepts to various problems to solidify your understanding. Whether you're simplifying fractions, calculating percentages, or working with ratios, the ability to confidently handle these calculations empowers you to approach various mathematical challenges with ease and accuracy. The journey of mathematical understanding is continuous, and this exploration of "20 of 32" serves as a valuable stepping stone.
Latest Posts
Latest Posts
-
6 Pints How Many Gallons
Sep 11, 2025
-
Largest Dams In The Us
Sep 11, 2025
-
Veterans Stand Down Schedule 2024
Sep 11, 2025
-
The Outsiders Book Chapter 1
Sep 11, 2025
-
Days And Months In Spanish
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.