What Is .2 Of 1000
scising
Sep 06, 2025 · 5 min read
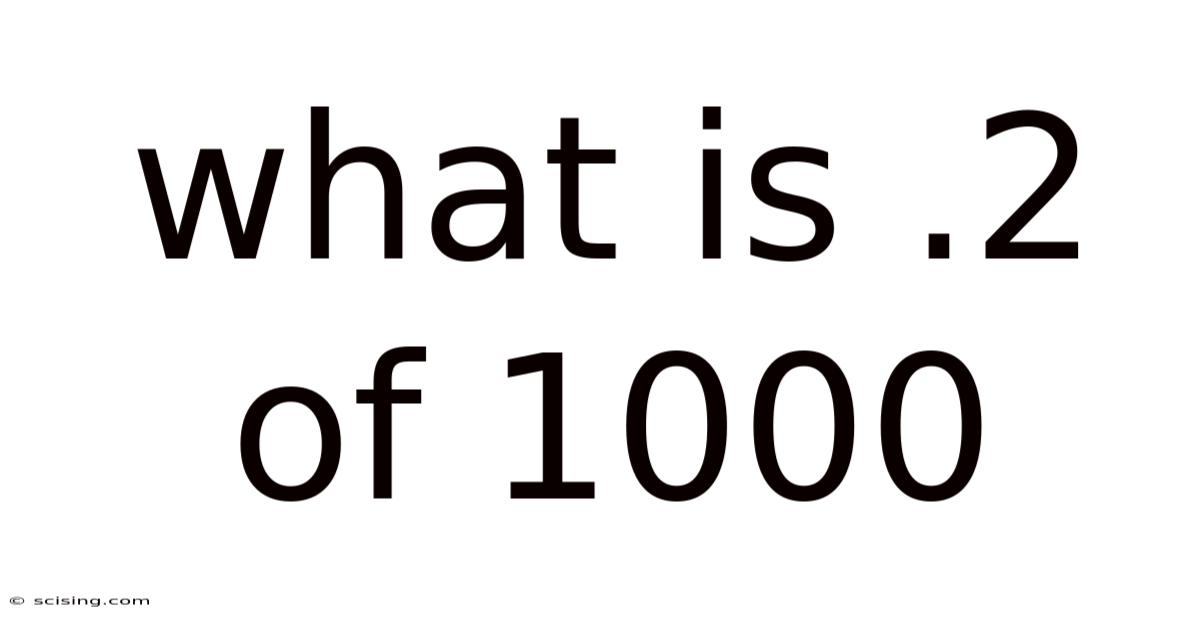
Table of Contents
What is 0.2 of 1000? Unpacking Percentages and Proportions
Finding 0.2 of 1000 might seem like a simple calculation, a quick task for a calculator. However, understanding the underlying principles behind this seemingly straightforward problem unlocks a world of practical applications in everyday life, from calculating discounts and taxes to understanding financial statements and scientific data. This article delves into the calculation itself, explains the mathematical concepts involved, explores different methods for solving similar problems, and provides examples to solidify your understanding. We'll also address frequently asked questions and delve into the broader implications of understanding proportions and percentages.
Understanding the Problem: 0.2 of 1000
The question "What is 0.2 of 1000?" is essentially asking for 0.2 times 1000. The word "of" in this context signifies multiplication. This is a fundamental concept in mathematics, applicable across various fields. We can rephrase the question as: "What is 20% of 1000?" since 0.2 is equivalent to 20/100 or 20%. This equivalence highlights the interchangeability of decimals and percentages, which are simply different ways of representing the same proportion.
Method 1: Direct Multiplication
The most straightforward method involves direct multiplication:
0.2 x 1000 = 200
This calculation can be performed mentally, using a calculator, or even with pen and paper. Multiplying 0.2 by 1000 is equivalent to moving the decimal point in 0.2 three places to the right, resulting in 200.
Method 2: Converting to Percentage
As mentioned earlier, 0.2 is equivalent to 20%. Finding 20% of 1000 can be achieved in a few ways:
-
Using the fraction equivalent: 20% can be written as the fraction 20/100. To find 20% of 1000, we calculate (20/100) * 1000. Simplifying the fraction to 1/5, we get (1/5) * 1000 = 200.
-
Using the decimal equivalent: We've already established that 20% is equal to 0.2. Therefore, 20% of 1000 is 0.2 * 1000 = 200.
-
Using the percentage formula: The basic percentage formula is: (Percentage/100) * Total Value. In our case, this translates to (20/100) * 1000 = 200.
Method 3: Proportions
The problem can also be solved using proportions. We can set up a proportion:
x / 1000 = 0.2 / 1
Where 'x' represents the unknown value we're trying to find (0.2 of 1000). To solve for x, we cross-multiply:
x * 1 = 0.2 * 1000
x = 200
This method demonstrates the relationship between parts and the whole, showcasing the proportional nature of the problem.
Expanding the Understanding: Real-World Applications
The ability to calculate percentages and proportions is crucial in numerous real-world scenarios:
-
Finance: Calculating interest earned on savings accounts, determining the discount on sale items, understanding tax rates, analyzing financial statements, and calculating loan repayments all involve these fundamental mathematical concepts. For example, a 5% discount on a $1000 item would be calculated as 0.05 * $1000 = $50.
-
Science: Many scientific calculations rely on percentages and proportions. For instance, expressing the concentration of a solution (e.g., 20% saline solution), calculating the percentage error in an experiment, and analyzing statistical data frequently involve these concepts.
-
Everyday Life: Calculating tips at restaurants, determining the amount of ingredients needed for a recipe, understanding sales and discounts, and many other everyday tasks require a solid grasp of percentages and proportions.
Beyond the Basics: Dealing with More Complex Scenarios
While the example of 0.2 of 1000 is relatively simple, the underlying principles can be applied to more complex calculations. Consider these examples:
-
Finding a percentage of a percentage: For example, finding 15% of 20% of 1000. This would involve a two-step calculation: First, find 20% of 1000 (200), then find 15% of 200 (30).
-
Calculating percentage increase or decrease: Suppose a value increases by 10% from 1000. The increase is 10% of 1000, which is 100. The new value is 1000 + 100 = 1100. Similarly, a 10% decrease from 1000 would result in a new value of 900.
-
Finding the original value given a percentage: If a discounted item costs $800 after a 20% discount, you can find the original price using the following equation: x - 0.2x = 800, where x is the original price. Solving for x gives x = 1000.
-
Working with multiple percentages: Imagine calculating the final price after a 10% discount followed by a 5% sales tax. This would require multiple steps, applying each percentage sequentially.
Frequently Asked Questions (FAQ)
Q: What is the difference between 0.2 and 20%?
A: They represent the same proportion. 0.2 is the decimal form, while 20% is the percentage form. They are interchangeable, depending on the context and the desired method of calculation.
Q: Can I use a calculator for these types of problems?
A: Absolutely! Calculators are efficient tools for handling these calculations, particularly when dealing with more complex scenarios or larger numbers.
Q: How can I improve my understanding of percentages and proportions?
A: Practice is key! Try solving various problems involving percentages and proportions, starting with simple examples and gradually increasing the complexity. Online resources, textbooks, and educational websites offer numerous practice problems and tutorials.
Q: Are there any online tools or calculators specifically designed for percentage calculations?
A: Yes, many websites and applications offer online percentage calculators that can automate these calculations. These calculators can be particularly helpful for more complex problems.
Conclusion: Mastering Percentages and Proportions
Understanding the calculation of 0.2 of 1000, and more broadly, the concepts of percentages and proportions, is a fundamental skill with far-reaching applications. This knowledge extends beyond simple arithmetic; it equips you with the tools to analyze data, make informed decisions, and navigate various aspects of everyday life and professional endeavors. By mastering these fundamental concepts and practicing different calculation methods, you'll be well-equipped to tackle a wide array of mathematical problems, from straightforward calculations to more complex scenarios. Remember that consistent practice is the key to solidifying your understanding and building confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Difference Between Disciple And Apostle
Sep 06, 2025
-
Is Grass Abiotic Or Biotic
Sep 06, 2025
-
8 Percent As A Decimal
Sep 06, 2025
-
Enthalpy Of Fusion Of Ice
Sep 06, 2025
-
Great Gatsby Chapter 7 Summary
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Is .2 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.