What Is 2/3 Plus 2/3
scising
Sep 20, 2025 · 5 min read
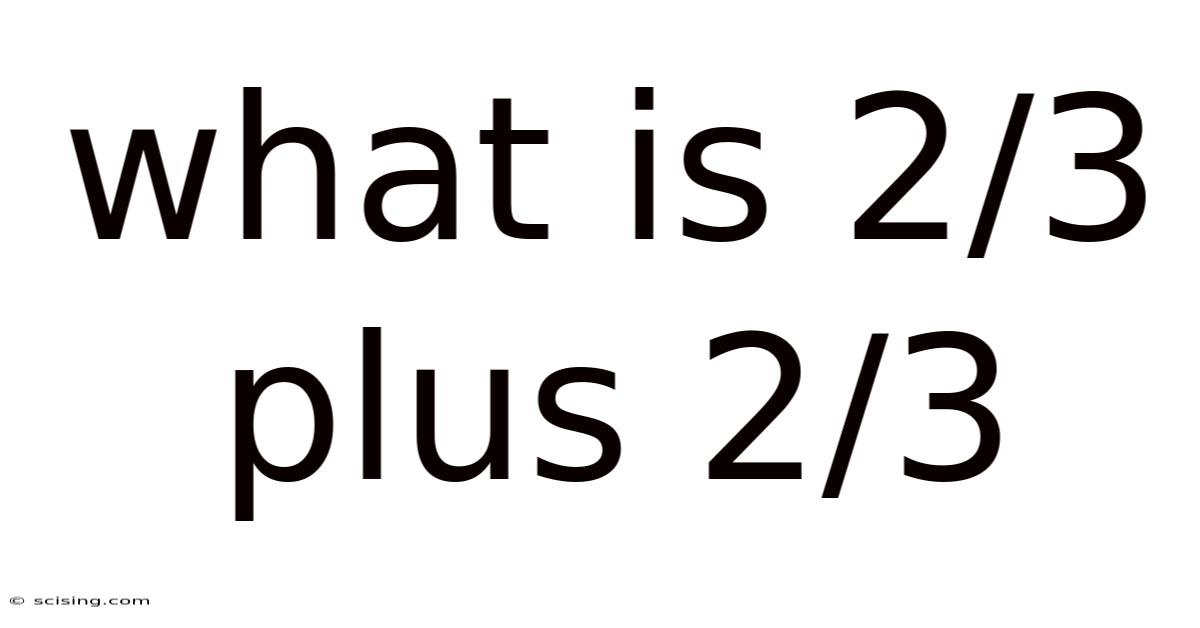
Table of Contents
What is 2/3 Plus 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple question, "What is 2/3 plus 2/3?" While the answer might seem obvious to some, we'll delve into a comprehensive explanation, covering the fundamental principles of fraction addition, different methods of solving the problem, real-world applications, and addressing common misconceptions. This exploration will solidify your understanding of fractions and provide a solid foundation for more complex mathematical concepts.
Introduction to Fractions
Before jumping into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written in the form a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 out of 3 equal parts.
Understanding fractions is crucial in various aspects of life, from baking and cooking (measuring ingredients) to construction (measuring materials) and even finance (understanding percentages and proportions). Mastering fraction addition is a stepping stone to more advanced mathematical concepts.
Adding Fractions: The Fundamental Principle
Adding fractions with the same denominator is straightforward. The key principle is that we only add the numerators while keeping the denominator the same. Think of it like this: if you have 2 apples out of 3 (2/3) and you add another 2 apples out of the same 3 (2/3), you now have a total of 4 apples out of 3 (4/3).
Mathematically, this is represented as:
2/3 + 2/3 = (2 + 2) / 3 = 4/3
Solving 2/3 + 2/3: Step-by-Step
Let's break down the solution to our problem:
-
Identify the Denominators: Both fractions have the same denominator, which is 3. This simplifies the addition process significantly.
-
Add the Numerators: Add the numerators together: 2 + 2 = 4.
-
Maintain the Denominator: Keep the denominator the same: 3.
-
Combine: The result is 4/3.
Therefore, 2/3 + 2/3 = 4/3.
Understanding Improper Fractions and Mixed Numbers
The result, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3). Improper fractions are perfectly valid, but they're often converted into mixed numbers for easier interpretation.
A mixed number combines a whole number and a proper fraction. To convert 4/3 into a mixed number:
-
Divide the numerator by the denominator: 4 divided by 3 is 1 with a remainder of 1.
-
Write the result: The whole number is 1 (the quotient), and the remaining fraction is 1/3 (the remainder over the original denominator).
Therefore, 4/3 is equal to 1 1/3. This means we have one whole unit and one-third of another unit.
Visual Representation
Visual aids can significantly improve understanding, especially when dealing with fractions. Imagine a circle divided into three equal parts. 2/3 would represent two of those three parts shaded. Adding another 2/3 would mean shading two more parts. The result is all three parts shaded (one whole circle) plus one more part shaded from a second circle (1 1/3).
Real-World Applications of Fraction Addition
Understanding fraction addition has various real-world applications:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractions is essential to correctly calculate the total amount of an ingredient needed when combining multiple recipes or scaling a recipe up or down.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Adding fractions is used to calculate total lengths, areas, and volumes.
-
Finance: Fractions are frequently used in financial calculations, such as calculating proportions of investments, determining interest rates, or understanding stock market changes.
-
Data Analysis: Fractions and their addition are essential for representing and analyzing data in various fields, including science and statistics. For example, expressing proportions of a population or results from an experiment.
Different Methods for Adding Fractions
While the direct method of adding numerators with a common denominator is the simplest, other methods can be helpful depending on the context:
-
Using a Number Line: A number line can visualize the addition process. Start at 2/3 on the number line and move 2/3 units further to reach 4/3 (or 1 1/3).
-
Using Diagrams: Diagrams, such as circles or rectangles divided into equal parts, provide a visual representation of the addition, helping to reinforce the concept.
-
Using Decimal Conversion: Fractions can be converted to decimals, making the addition more intuitive for some individuals. 2/3 is approximately 0.667, and 0.667 + 0.667 = 1.334, which is close to 1 1/3. However, this method introduces rounding errors.
Addressing Common Misconceptions
Several common misconceptions surround fraction addition:
-
Adding denominators: A common mistake is to add both the numerators and denominators. Remember, only the numerators are added; the denominator remains the same (when adding fractions with like denominators).
-
Improper fraction simplification: Always simplify improper fractions to mixed numbers for easier understanding and interpretation.
-
Difficulty visualizing fractions: Use visual aids and real-world examples to build a better intuitive understanding of fractions and their operations.
Frequently Asked Questions (FAQs)
-
What if the denominators are different? If the denominators are different, you need to find a common denominator before adding the fractions. This involves finding the least common multiple (LCM) of the denominators.
-
Can I add fractions and whole numbers? Yes, you can. First, convert the whole number into a fraction with the same denominator as the fraction you're adding it to. Then, add the numerators.
-
What are some real-world examples besides the ones you mentioned? Fraction addition is used in tailoring (measuring fabric), carpentry (measuring wood), and even in music (understanding rhythm and time signatures).
Conclusion
Adding 2/3 and 2/3 results in 4/3, which is equivalent to the mixed number 1 1/3. This seemingly simple calculation underscores the fundamental principles of fraction addition, highlighting the importance of understanding numerators, denominators, improper fractions, and mixed numbers. By mastering this concept, you'll be well-prepared to tackle more complex mathematical problems and confidently apply fraction addition in various real-world scenarios. Remember to always visualize, understand the underlying principles, and practice regularly to solidify your understanding of fractions. The journey of learning mathematics is often filled with small victories, and mastering fraction addition is one such important milestone.
Latest Posts
Latest Posts
-
Food Chain Of A Forest
Sep 20, 2025
-
Across 5 Aprils Study Guide
Sep 20, 2025
-
How To Compute Slope Percentage
Sep 20, 2025
-
Cause And Effect Essay Ideas
Sep 20, 2025
-
Quinary Sector Ap Human Geography
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Plus 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.