What Is 2/3 Of 30
scising
Sep 25, 2025 · 5 min read
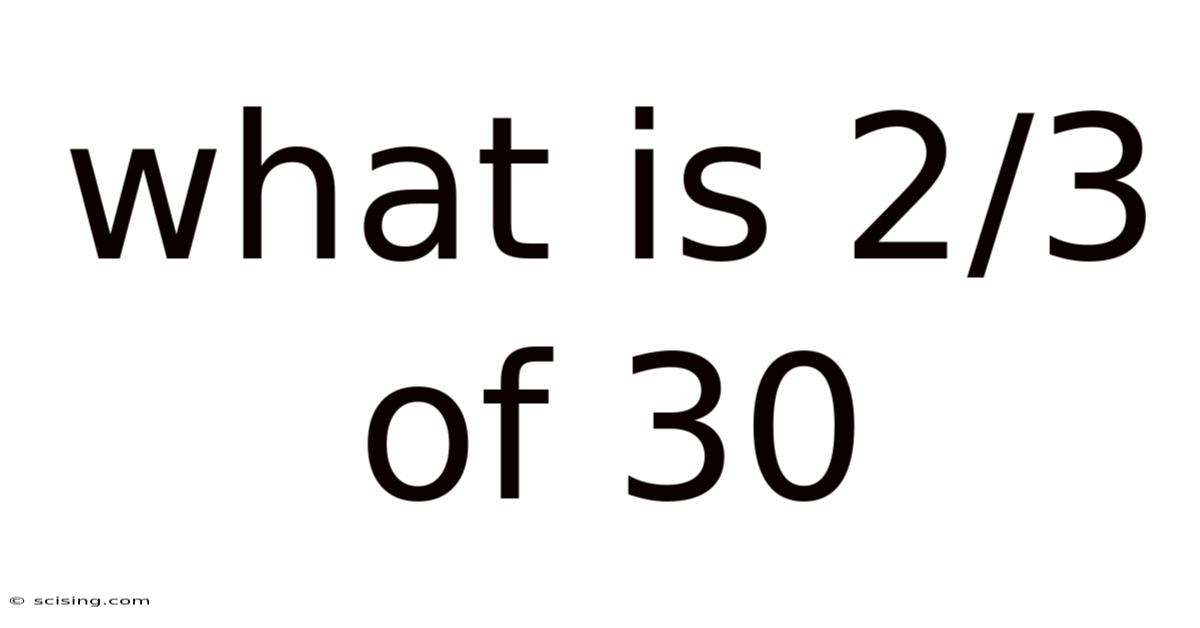
Table of Contents
What is 2/3 of 30? A Deep Dive into Fractions and Their Applications
Finding 2/3 of 30 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic question unlocks a deeper understanding of fractions, their practical applications, and their role in more complex mathematical concepts. This article will not only show you how to calculate 2/3 of 30 but also explore the underlying principles, offer alternative methods, and discuss the broader significance of fractional calculations in everyday life and advanced mathematics.
Understanding Fractions: A Refresher
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 2/3, the denominator 3 means the whole is divided into three equal parts, and the numerator 2 means we're considering two of those parts.
Calculating 2/3 of 30: The Direct Approach
The most straightforward method to calculate 2/3 of 30 is to use the following formula:
(Fraction) x (Whole Number) = Part
In our case:
(2/3) x 30 = ?
To solve this, we multiply the numerator (2) by the whole number (30), and then divide the result by the denominator (3):
(2 x 30) / 3 = 60 / 3 = 20
Therefore, 2/3 of 30 is 20.
Alternative Methods: Visualizing Fractions
While the direct approach is efficient, visualizing the problem can enhance understanding, especially for those who find abstract mathematical concepts challenging. We can represent the problem visually using various methods:
-
Using a circle or a rectangle: Divide a circle or rectangle into three equal parts. Shade two of those parts to represent 2/3. If the whole represents 30, then each part represents 30/3 = 10. Therefore, two parts represent 2 x 10 = 20.
-
Using a number line: Draw a number line from 0 to 30. Divide the line into three equal segments. Each segment represents 10 (30/3). Mark two segments to represent 2/3. The endpoint of the second segment will be at 20.
These visual aids make the concept of fractions more concrete and accessible, particularly for younger learners or those who prefer a more intuitive approach to problem-solving.
Understanding the Concept of "Of" in Mathematics
The word "of" in mathematical contexts, particularly when dealing with fractions and percentages, usually signifies multiplication. The phrase "2/3 of 30" is mathematically equivalent to "(2/3) x 30". This understanding is crucial for solving various problems involving fractions and percentages. Always remember that "of" translates to multiplication.
Extending the Concept: Working with Different Fractions and Numbers
The method described above can be applied to any fraction and any whole number. For instance, let's find 3/4 of 48:
(3/4) x 48 = (3 x 48) / 4 = 144 / 4 = 36
Therefore, 3/4 of 48 is 36.
Similarly, we can find 5/6 of 72:
(5/6) x 72 = (5 x 72) / 6 = 360 / 6 = 60
Therefore, 5/6 of 72 is 60.
Practice with different examples will solidify your understanding of how to calculate fractions of whole numbers.
Real-World Applications: Where Fractions Matter
Fractions are far from abstract mathematical concepts; they have practical applications across various aspects of our daily lives:
-
Cooking and Baking: Recipes often require fractional measurements, such as 1/2 cup of flour or 2/3 of a teaspoon of baking powder. Accurate fractional calculations are crucial for successful cooking and baking.
-
Shopping and Budgeting: Sales and discounts are often expressed as fractions or percentages (which are essentially fractions with a denominator of 100). Understanding fractions helps in calculating savings and budgeting effectively.
-
Construction and Engineering: Engineers and architects use fractions extensively in their blueprints and calculations to ensure precise measurements and designs.
-
Finance and Investments: Fractions and percentages are integral to understanding interest rates, stock prices, and investment returns.
-
Data Analysis and Statistics: Fractions and proportions are essential tools for analyzing data, interpreting statistical results, and making informed decisions based on data.
Beyond the Basics: Fractions in Advanced Mathematics
Fractions form the foundation for many advanced mathematical concepts:
-
Algebra: Fractions are used extensively in algebraic equations and manipulations.
-
Calculus: Derivatives and integrals often involve working with fractions and limits.
-
Probability and Statistics: Probability calculations heavily rely on fractions and proportions to represent chances and likelihoods of events.
Frequently Asked Questions (FAQ)
Q1: What if the fraction and the whole number don't simplify easily?
A: Even if the numbers don't simplify easily, the same method applies. You can still multiply the numerator by the whole number and then divide by the denominator. A calculator can be helpful in such cases.
Q2: Can I convert fractions to decimals before multiplying?
A: Yes, you can convert the fraction to a decimal and then multiply. For example, 2/3 is approximately 0.6667. So, 0.6667 x 30 ≈ 20. However, this method might introduce slight inaccuracies due to rounding. The direct approach using fractions is generally more precise.
Q3: Are there other ways to represent 2/3 of 30?
A: Yes, you can represent it as a decimal (20.0), a percentage (100% of 20), or even as a ratio (20:30, which can be simplified to 2:3). All these representations convey the same mathematical concept.
Conclusion: Mastering Fractions for a Brighter Future
Calculating 2/3 of 30, although seemingly simple, opens doors to a deeper understanding of fractions and their significant role in various aspects of mathematics and everyday life. From baking a cake to making informed financial decisions, mastering fractions is a crucial skill that enhances problem-solving capabilities and empowers individuals to tackle more complex mathematical concepts with confidence. Remember the fundamental principles, practice regularly with different examples, and embrace the visual methods to make the learning process engaging and effective. The more you practice, the more comfortable you'll become with fractions, paving the way for future success in mathematics and beyond.
Latest Posts
Latest Posts
-
Chapter 2 Summary Great Gatsby
Sep 25, 2025
-
Visual Aids For A Speech
Sep 25, 2025
-
Surface Area Of Hexagonal Prism
Sep 25, 2025
-
Pictures Of Bees And Wasps
Sep 25, 2025
-
Que Sera Sera What Language
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.