What Is 15 Of 3
scising
Sep 08, 2025 · 5 min read
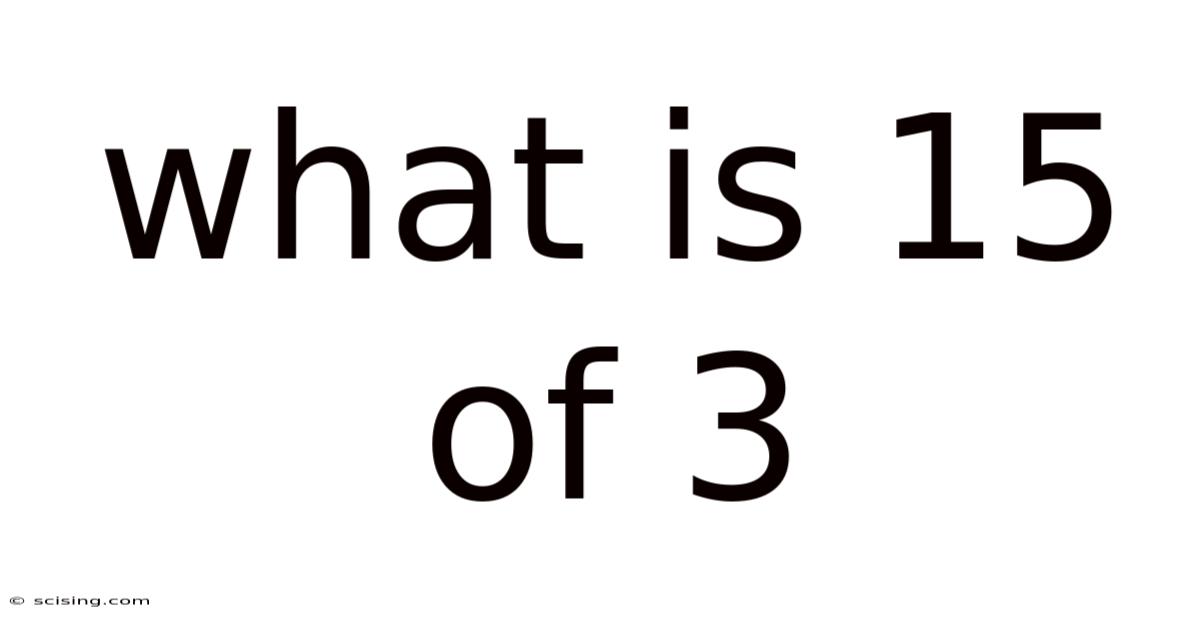
Table of Contents
What is 15 of 3? Demystifying Fractions and Percentages
The question "What is 15 of 3?" might seem deceptively simple at first glance. However, it opens the door to understanding fundamental mathematical concepts like fractions, percentages, and the crucial difference between of meaning multiplication versus other mathematical operations. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, providing a solid foundation for anyone looking to improve their mathematical literacy.
Understanding the Question: "Of" as Multiplication
The word "of" in mathematical contexts, particularly when dealing with fractions and percentages, almost always indicates multiplication. Therefore, "15 of 3" translates directly into the mathematical expression: 15 * 3. This seemingly straightforward translation, however, often causes confusion when "15" is not a whole number but instead represents a fraction or a percentage. Let's break down the scenarios:
Scenario 1: 15 as a Whole Number
If "15" is a whole number, the calculation is simple: 15 multiplied by 3 equals 45. This is the most basic interpretation.
Scenario 2: 15 as a Fraction
The question becomes significantly more nuanced if "15" represents a fraction. For example:
-
"1/5 of 3": This translates to (1/5) * 3. To solve this, we multiply the numerator (1) by 3, keeping the denominator (5) the same: (3/5). Therefore, 1/5 of 3 is 3/5.
-
"15/100 of 3": This represents a fraction of 3. The calculation is (15/100) * 3 = 45/100. This fraction can be simplified to 9/20 or expressed as a decimal (0.45).
Scenario 3: 15 as a Percentage
If "15" represents 15%, the calculation involves converting the percentage to a decimal or fraction before multiplying.
- "15% of 3": First, convert 15% to a decimal by dividing by 100: 15% = 0.15. Then, multiply 0.15 by 3: 0.15 * 3 = 0.45. Alternatively, convert 15% to a fraction: 15/100. Then, multiply (15/100) * 3 = 45/100 = 0.45. Therefore, 15% of 3 is 0.45.
The Importance of Context: Clarifying Ambiguity
The ambiguity of the original question highlights the critical importance of context in mathematics. Without further information specifying whether "15" represents a whole number, a fraction, or a percentage, the question remains incomplete and has multiple valid answers depending on the interpretation. Precise language and clear notation are essential to avoid misunderstandings.
Delving Deeper: Fractions and Their Representation
To fully grasp the concept of "15 of 3," we need a solid understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, representing the number of parts being considered.
- Denominator: The bottom number, representing the total number of equal parts in the whole.
Understanding fractions is fundamental to various mathematical operations, including:
-
Simplification: Reducing a fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 45/100 simplifies to 9/20.
-
Addition and Subtraction: Fractions must have a common denominator before addition or subtraction can be performed.
-
Multiplication: Multiply the numerators together and the denominators together.
-
Division: Invert the second fraction (reciprocal) and multiply.
Percentages: A Special Case of Fractions
Percentages are a specific type of fraction where the denominator is always 100. They represent a proportion out of a hundred. Converting percentages to decimals or fractions simplifies calculations involving percentages. The conversion is straightforward:
-
Percentage to Decimal: Divide the percentage by 100. For example, 15% = 15/100 = 0.15
-
Decimal to Percentage: Multiply the decimal by 100. For example, 0.45 * 100 = 45%
-
Fraction to Percentage: Convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply by 100. For example, 3/5 = 0.6 * 100 = 60%
Practical Applications: Real-world Examples
Understanding fractions and percentages is crucial in various real-world situations, including:
-
Calculating discounts: Determining the final price of an item after a percentage discount.
-
Determining proportions: Understanding ratios and proportions in recipes, construction, and other fields.
-
Analyzing data: Interpreting data presented as percentages or fractions in charts and graphs.
-
Financial calculations: Computing interest rates, taxes, and other financial metrics.
Frequently Asked Questions (FAQ)
Q1: What if the question was "15% of 3 apples"?
A1: The mathematical calculation remains the same. 15% of 3 = 0.45. However, the context adds a real-world element. You can't have 0.45 apples, so you would need to round down to 0 apples or consider the context – perhaps you are dealing with the weight of the apples, where 0.45 could represent a fraction of a pound or kilogram.
Q2: How do I solve more complex problems involving fractions and percentages?
A2: Practice is key. Start with simpler problems and gradually increase the complexity. Use online resources, textbooks, and practice exercises to build your skills. Focus on understanding the underlying concepts, not just memorizing formulas.
Q3: Are there any online tools or calculators that can help?
A3: Many online calculators and resources are available for performing calculations involving fractions and percentages. These tools can be particularly helpful for verifying your work and exploring different approaches.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 15 of 3?" ultimately underscores the importance of clear communication, precise mathematical notation, and a thorough understanding of fundamental concepts like fractions and percentages. By mastering these concepts, you not only solve this specific problem but equip yourself with the essential mathematical skills necessary to tackle a wide range of problems in various fields. Remember that the key is not just finding the answer but understanding the why behind the calculation. This approach fosters a deeper appreciation for mathematics and its practical applications in everyday life. Consistent practice and a focus on understanding the underlying principles are the keys to success in mastering these essential mathematical skills. Keep practicing, and you’ll soon find these calculations intuitive and effortless.
Latest Posts
Latest Posts
-
Is Co32 Polar Or Nonpolar
Sep 08, 2025
-
How Many Ounces 1 Gallon
Sep 08, 2025
-
As You Like It Synopsis
Sep 08, 2025
-
What Is The Conditioned Stimulus
Sep 08, 2025
-
What Does 10th Percentile Mean
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.