What Is 15 Of 20
scising
Sep 15, 2025 · 6 min read
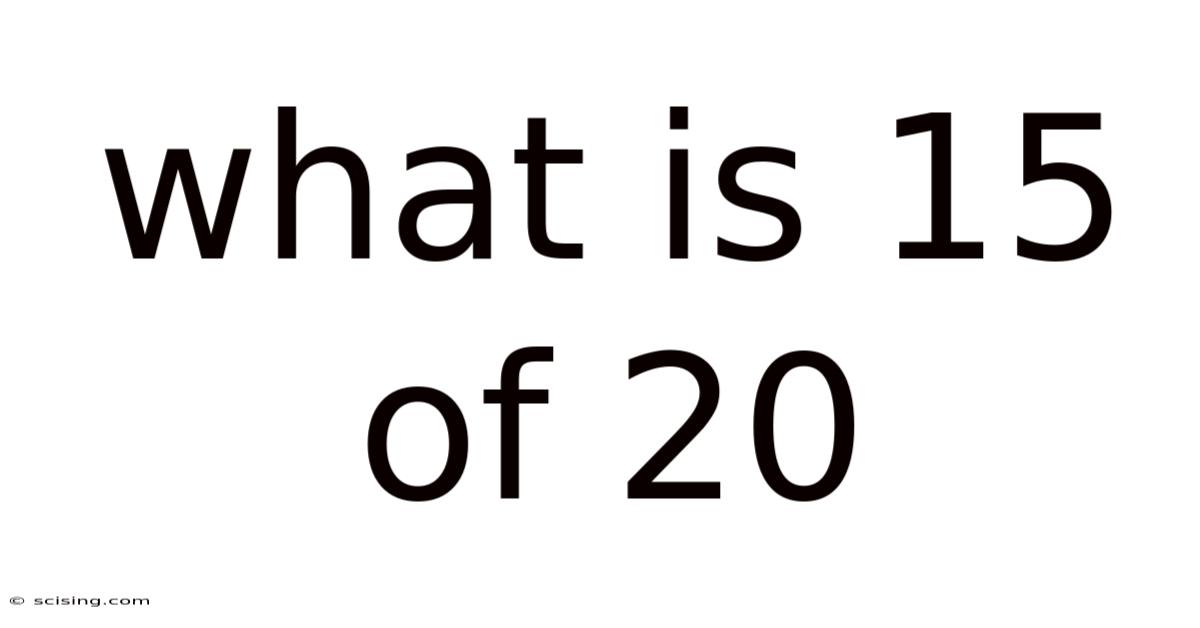
Table of Contents
What is 15 of 20? Understanding Fractions, Percentages, and Ratios
This article delves into the seemingly simple question, "What is 15 of 20?" While the immediate answer might seem obvious – it's a part of a whole – understanding this question fully opens doors to a deeper comprehension of fundamental mathematical concepts like fractions, percentages, and ratios. We'll explore these concepts, demonstrating how they interconnect and how to solve similar problems confidently. This understanding is crucial for various applications, from everyday calculations to advanced scientific and financial analyses.
Introduction: Deconstructing the Question
The question "What is 15 of 20?" essentially asks us to determine the relationship between the number 15 and the number 20. This relationship can be expressed in several ways, each offering a unique perspective on the problem. We'll explore three primary methods: expressing the relationship as a fraction, converting it into a percentage, and understanding it as a ratio.
Understanding Fractions: Representing Parts of a Whole
The most straightforward way to represent "15 of 20" is as a fraction. A fraction expresses a part of a whole. In this case, 15 represents the part and 20 represents the whole. Therefore, the fraction is written as 15/20.
This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (20). The GCD of 15 and 20 is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction 3/4. This means that 15 is three-quarters (¾) of 20.
Simplifying Fractions: Simplifying fractions is essential for clarity and ease of understanding. A simplified fraction represents the same value as the original fraction but in its most concise form. It's crucial to always simplify fractions whenever possible.
Converting Fractions to Percentages: Expressing Proportion in Hundredths
While fractions are useful, percentages offer a standardized way to compare proportions. Percentages express a fraction as a portion of 100. To convert the fraction 3/4 (or 15/20) to a percentage, we perform the following calculation:
(3/4) * 100% = 75%
Therefore, 15 is 75% of 20. This means that 15 represents 75 out of every 100 parts of 20.
Converting Fractions to Percentages: This process involves dividing the numerator by the denominator and then multiplying the result by 100%. It provides a readily understandable representation of the proportional relationship.
Understanding Ratios: Comparing Two Quantities
A ratio expresses the relationship between two quantities. In this case, the ratio of 15 to 20 can be written as 15:20 or 15/20. Similar to fractions, ratios can also be simplified by finding the GCD. Simplifying 15:20 gives us the ratio 3:4. This ratio indicates that for every 3 units of one quantity, there are 4 units of the other quantity.
Ratios vs. Fractions: While fractions and ratios are closely related and often used interchangeably, there's a subtle difference. Fractions represent a part of a whole, whereas ratios compare two quantities. However, both can be used to express proportional relationships.
Real-World Applications: Where This Knowledge Matters
The concepts of fractions, percentages, and ratios are fundamental to numerous aspects of daily life and various professional fields. Here are a few examples:
-
Shopping: Calculating discounts, comparing prices, and determining the best value for money often involve percentage calculations. For example, a 25% discount on a $20 item would be a $5 discount, leaving a final price of $15.
-
Cooking: Following recipes often requires understanding ratios and fractions. For instance, a recipe might call for a 2:1 ratio of flour to sugar, or ½ cup of milk.
-
Finance: Understanding percentages is critical for managing personal finances. Calculating interest rates, understanding loan repayments, and analyzing investment returns all depend heavily on this knowledge.
-
Science: Many scientific calculations involve ratios and percentages, for example, expressing concentrations of solutions or calculating reaction yields.
-
Data Analysis: Percentages and ratios are essential tools for interpreting data and presenting findings in a clear and concise manner. This is crucial in fields like market research, statistics, and epidemiology.
Solving Similar Problems: A Step-by-Step Guide
Let's apply the knowledge gained to solve similar problems. Suppose we want to find what part of 30 is 18. We can follow these steps:
-
Express as a Fraction: The fraction representing 18 of 30 is 18/30.
-
Simplify the Fraction: The GCD of 18 and 30 is 6. Dividing both numerator and denominator by 6 gives us the simplified fraction 3/5.
-
Convert to Percentage: (3/5) * 100% = 60%
-
Express as a Ratio: The ratio is 18:30, which simplifies to 3:5.
Therefore, 18 is 3/5 or 60% of 30, and the ratio of 18 to 30 is 3:5.
Advanced Concepts: Proportions and Direct/Inverse Relationships
Understanding "15 of 20" leads us to explore more advanced mathematical relationships, such as proportions. A proportion is a statement that two ratios are equal. For example:
15/20 = 3/4
This equation shows a proportion; the ratio of 15 to 20 is equal to the ratio of 3 to 4. Proportions are essential for solving problems involving scaling, similar shapes, and other applications where the relationship between quantities remains constant.
Further, we can explore direct and inverse relationships. A direct relationship means that as one quantity increases, the other quantity increases proportionally. An inverse relationship means that as one quantity increases, the other quantity decreases proportionally. Understanding these relationships enhances problem-solving abilities significantly.
Frequently Asked Questions (FAQ)
Q: What is the difference between a fraction and a ratio?
A: While often used interchangeably, fractions represent a part of a whole, while ratios compare two quantities. Both express proportional relationships but have slightly different interpretations.
Q: Can I use a calculator to solve these problems?
A: Yes, calculators can be very helpful for simplifying fractions, converting fractions to percentages, and performing other calculations quickly. However, understanding the underlying concepts is crucial for problem-solving and interpreting the results meaningfully.
Q: Are there any online resources for practicing these concepts?
A: Many websites and educational platforms offer interactive exercises and tutorials on fractions, percentages, and ratios. These resources can provide valuable practice and reinforcement of the concepts learned.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and compare. A simplified fraction represents the same value as the original fraction but in its most concise form. This improves clarity and makes further calculations simpler.
Conclusion: Mastering Fundamental Mathematical Concepts
Understanding "What is 15 of 20?" transcends a simple arithmetic problem. It provides a gateway to comprehending fundamental mathematical concepts – fractions, percentages, and ratios – that are essential for navigating various aspects of life. By mastering these concepts, you equip yourself with powerful tools for problem-solving, critical thinking, and analytical reasoning. The ability to confidently work with fractions, percentages, and ratios extends far beyond the classroom, proving invaluable in diverse professional fields and everyday situations. Continuous practice and application are key to solidifying your understanding and building confidence in applying these fundamental mathematical tools.
Latest Posts
Latest Posts
-
What Is Teacher In Spanish
Sep 15, 2025
-
Are Millimeters Smaller Than Centimeters
Sep 15, 2025
-
270 Km H To Mph
Sep 15, 2025
-
149 Weeks Ago From Today
Sep 15, 2025
-
What Is 70mm In Inches
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.