What Is 12 Of 75
scising
Sep 20, 2025 · 5 min read
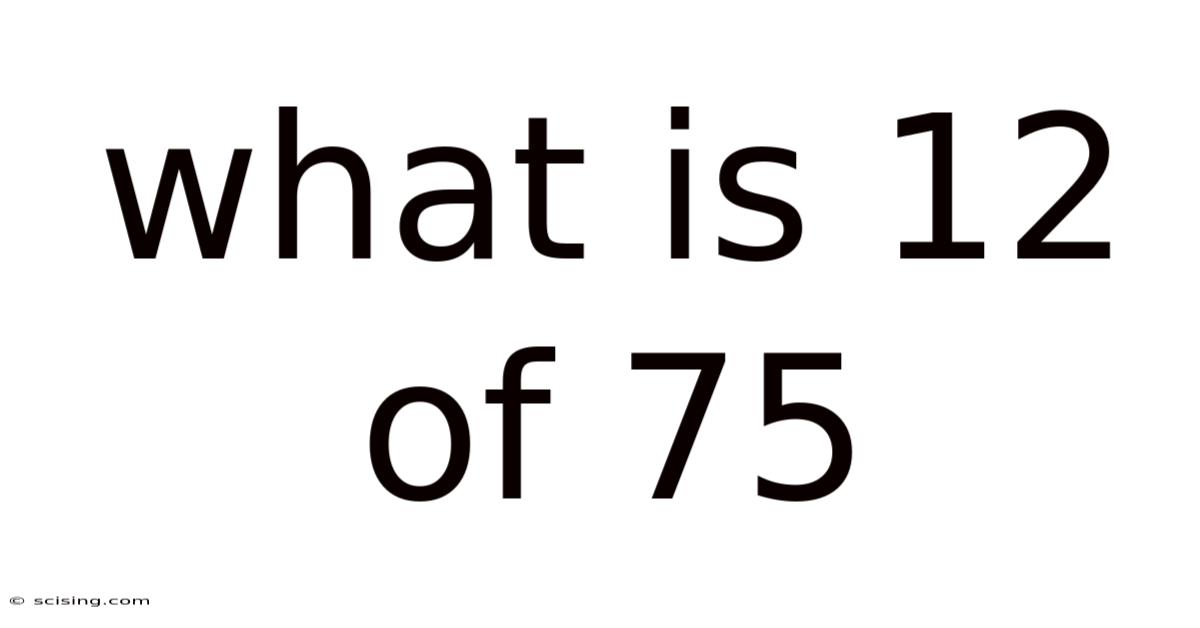
Table of Contents
What is 12/75? Unpacking Fractions, Decimals, and Percentages
Understanding fractions, decimals, and percentages is a fundamental skill in mathematics, applicable across various fields from everyday budgeting to complex scientific calculations. This comprehensive guide will not only answer the question "What is 12/75?" but also delve into the underlying concepts, providing you with a solid foundation for tackling similar problems in the future. We'll explore different methods of calculation, discuss the relationship between fractions, decimals, and percentages, and even touch upon real-world applications.
Introduction: Understanding the Fraction 12/75
The fraction 12/75 represents twelve parts out of a total of seventy-five equal parts. This seemingly simple fraction presents a great opportunity to explore fundamental mathematical concepts and techniques. We will learn how to simplify this fraction to its lowest terms, convert it to a decimal, and then express it as a percentage. Mastering these conversions is crucial for understanding numerical relationships and applying them effectively in various contexts.
Method 1: Simplifying the Fraction
Before converting 12/75 to a decimal or percentage, it's beneficial to simplify the fraction. Simplifying means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of both the numerator (12) and the denominator (75). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 12 and 75, we can use the prime factorization method:
- Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
- Prime factorization of 75: 3 x 5 x 5 (or 3 x 5²)
The common factor between 12 and 75 is 3. Dividing both the numerator and the denominator by 3, we get:
12 ÷ 3 = 4 75 ÷ 3 = 25
Therefore, the simplified fraction is 4/25. This simplified form is equivalent to the original fraction 12/75, meaning they represent the same value. Working with simplified fractions makes further calculations easier and results in cleaner answers.
Method 2: Converting the Fraction to a Decimal
To convert the simplified fraction 4/25 to a decimal, we perform a simple division:
4 ÷ 25 = 0.16
Therefore, the decimal equivalent of 12/75 is 0.16. This decimal representation is a concise and readily understandable form, particularly useful in calculations involving other decimal numbers.
Method 3: Converting the Fraction to a Percentage
Converting a fraction or decimal to a percentage involves multiplying by 100%. Starting with our simplified fraction 4/25, we can perform the calculation:
(4/25) x 100% = 16%
Alternatively, using the decimal equivalent 0.16:
0.16 x 100% = 16%
Thus, 12/75 is equivalent to 16%. Percentages are commonly used to represent proportions or ratios, making them valuable for comparing quantities and expressing probabilities.
Understanding the Relationship Between Fractions, Decimals, and Percentages
These three representations – fractions, decimals, and percentages – are interconnected and interchangeable. They all express parts of a whole, but they differ in their form and application:
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). They are precise and often used in mathematical calculations.
-
Decimals: Represent a part of a whole using a base-ten system. They are convenient for calculations involving addition, subtraction, multiplication, and division.
-
Percentages: Represent a part of a whole as a fraction of 100. They are commonly used for expressing proportions and comparing quantities, often seen in statistics, finance, and everyday life.
Real-World Applications of Fractions, Decimals, and Percentages
The concepts of fractions, decimals, and percentages are fundamental to numerous real-world applications:
-
Finance: Calculating interest rates, discounts, tax percentages, and profit margins.
-
Cooking and Baking: Measuring ingredients accurately using fractions and decimals.
-
Statistics: Analyzing data, representing probabilities, and calculating proportions.
-
Science: Measuring quantities, calculating concentrations, and interpreting experimental results.
-
Engineering: Designing structures, calculating dimensions, and assessing tolerances.
-
Everyday Life: Dividing expenses, calculating tips, and understanding discounts.
Further Exploration: Working with More Complex Fractions
While 12/75 is a relatively straightforward example, understanding the principles involved allows you to tackle more complex fractions. For example, let's consider the fraction 27/108:
- Find the GCD: The GCD of 27 and 108 is 27.
- Simplify the fraction: 27/108 simplifies to 1/4.
- Convert to decimal: 1/4 = 0.25
- Convert to percentage: 0.25 x 100% = 25%
This example demonstrates the consistent application of the steps involved in simplifying, converting to decimals, and converting to percentages. The key is to master the fundamental concepts of GCD, division, and multiplication.
Frequently Asked Questions (FAQs)
-
Q: What if the fraction cannot be simplified? A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. You can then proceed directly to converting it to a decimal and a percentage.
-
Q: How do I convert a decimal to a fraction? A: To convert a decimal to a fraction, write the decimal as the numerator over a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.), corresponding to the number of decimal places. Then, simplify the fraction to its lowest terms. For example, 0.75 = 75/100 = 3/4.
-
Q: How do I convert a percentage to a fraction or decimal? A: To convert a percentage to a fraction, divide the percentage by 100 and simplify. To convert a percentage to a decimal, divide the percentage by 100. For example, 60% = 60/100 = 3/5 = 0.6.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes calculations easier, reduces errors, and presents the result in a more concise and understandable form.
Conclusion: Mastering Fractions, Decimals, and Percentages
This detailed explanation of 12/75 has hopefully provided a clear understanding of the processes involved in simplifying fractions, converting them to decimals and percentages, and the underlying mathematical principles. The ability to effortlessly navigate these conversions is a cornerstone of mathematical literacy, applicable in various academic and professional settings. Remember to practice regularly, and you'll soon master these fundamental skills, paving the way for more advanced mathematical concepts. The seemingly simple question "What is 12/75?" opens a door to a deeper understanding of a crucial area of mathematics, equipping you with skills that will serve you well throughout life.
Latest Posts
Latest Posts
-
How Long Is 78 Inches
Sep 20, 2025
-
What Is A Social Theory
Sep 20, 2025
-
Statue Of Jupiter At Olympia
Sep 20, 2025
-
The Sleeper Edgar Allan Poe
Sep 20, 2025
-
Cute Spanish Nicknames For Guys
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.