What Is 12 Of 48
scising
Sep 21, 2025 · 5 min read
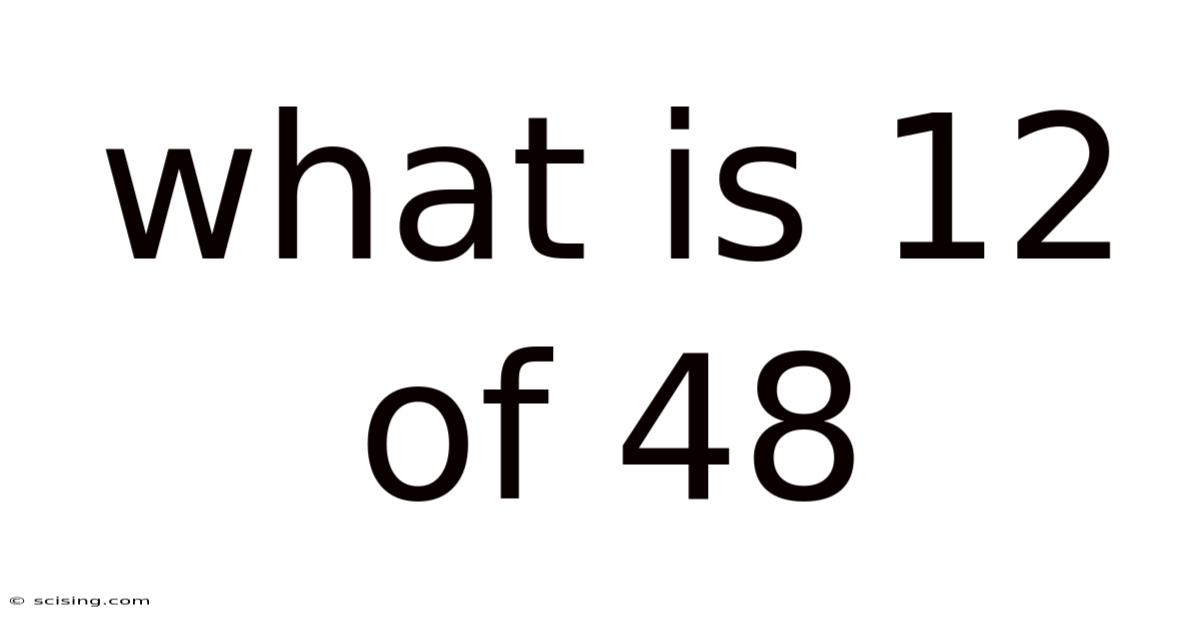
Table of Contents
What is 12 of 48? Unpacking Fractions, Percentages, and Ratios
Finding "12 of 48" might seem like a simple question, but it opens a door to a world of mathematical concepts crucial for everyday life. This seemingly straightforward query allows us to explore fractions, percentages, and ratios – fundamental building blocks of arithmetic and beyond. This article will delve deep into understanding what "12 of 48" represents, illustrating its meaning through various mathematical lenses and showcasing its practical applications.
Understanding the Basic Concept: Fractions
At its core, "12 of 48" represents a fraction. A fraction shows a part of a whole. In this case, 12 is the part and 48 is the whole. We can express this as 12/48. This fraction signifies that we're considering 12 units out of a total of 48 units.
Think of it like this: imagine you have 48 cookies, and you eat 12 of them. The fraction 12/48 represents the portion of cookies you consumed.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
The fraction 12/48 isn't in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of both the numerator (12) and the denominator (48). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 12 and 48, we can use several methods:
-
Listing Factors: List all the factors of 12 (1, 2, 3, 4, 6, 12) and 48 (1, 2, 3, 4, 6, 8, 12, 16, 24, 48). The largest number common to both lists is 12.
-
Prime Factorization: Break down both numbers into their prime factors.
- 12 = 2 x 2 x 3
- 48 = 2 x 2 x 2 x 2 x 3 The common prime factors are 2 x 2 x 3 = 12. Therefore, the GCD is 12.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. Repeatedly divide the larger number by the smaller number and replace the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Once we've found the GCD (12), we divide both the numerator and the denominator by it:
12 ÷ 12 = 1 48 ÷ 12 = 4
Therefore, the simplified fraction is 1/4. This means that 12 out of 48 is equivalent to 1 out of 4, or one-quarter.
Representing "12 of 48" as a Percentage
Percentages are another way to express parts of a whole. A percentage represents a fraction out of 100. To convert the fraction 12/48 (or its simplified form, 1/4) to a percentage, we perform the following calculation:
(1/4) x 100% = 25%
So, 12 out of 48 is equivalent to 25%. This signifies that 12 represents 25% of the total 48.
Understanding Ratios
The relationship between 12 and 48 can also be expressed as a ratio. A ratio compares two or more quantities. In this case, the ratio is 12:48. Similar to fractions, we can simplify this ratio by dividing both numbers by their GCD (12):
12 ÷ 12 = 1 48 ÷ 12 = 4
The simplified ratio is 1:4. This means that for every 1 unit, there are 4 units in total. This ratio is identical in meaning to the fraction 1/4 and the percentage 25%.
Practical Applications: Real-World Examples
The concept of finding "12 of 48" has numerous practical applications in various fields:
-
Business and Finance: Calculating profit margins, market share, or the proportion of expenses to revenue often involves working with fractions and percentages. For example, if a company sold 12 units out of a possible 48, they achieved a 25% sales rate.
-
Science: In scientific experiments, researchers frequently analyze data involving proportions and ratios. For instance, if 12 out of 48 samples tested positive, the positive rate is 25%.
-
Everyday Life: Dividing a pizza, sharing sweets, or calculating discounts all require understanding fractions and percentages. If you have 48 candies and you want to give 25% to a friend, you would give them 12 candies.
-
Cooking and Baking: Following recipes often involves ratios and proportions. If a recipe calls for a 1:4 ratio of sugar to flour, and you're using 12 grams of sugar, you would need 48 grams of flour.
Deeper Dive: Decimal Representation
The fraction 1/4 can also be represented as a decimal: 0.25. This decimal represents 25 hundredths, which is equivalent to 25%. The decimal representation is particularly useful for calculations involving computers and other digital systems.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Yes! You can use a calculator to divide 12 by 48 (12/48 = 0.25) and then multiply by 100 to obtain the percentage (0.25 x 100% = 25%). Alternatively, many calculators have a built-in function to simplify fractions.
Q: What if the numbers are larger?
A: The same principles apply even with larger numbers. Find the GCD of the numerator and denominator to simplify the fraction, and then convert to a percentage or decimal as needed.
Q: Are fractions, percentages, and ratios always interchangeable?
A: While they represent the same underlying concept of proportional relationships, the context might favor one form over the others. Percentages are commonly used for expressing proportions relative to a whole, whereas ratios emphasize the comparison between two or more quantities.
Q: What are some real-world examples besides those listed?
A: Consider calculating the percentage of students who passed an exam, determining the proportion of different types of fruits in a fruit bowl, or figuring out the ratio of ingredients in a paint mixture. In essence, anywhere you deal with parts of a whole or comparisons between quantities, fractions, percentages, and ratios become essential tools.
Conclusion: Mastering Proportional Reasoning
Understanding "12 of 48" extends beyond a simple arithmetic problem. It unlocks the power of proportional reasoning – a fundamental skill applicable in various facets of life. By mastering fractions, percentages, and ratios, you equip yourself with the tools to navigate numerical challenges effectively, whether in academic pursuits, professional endeavors, or everyday situations. This comprehensive understanding empowers you to approach complex problems with clarity and confidence, transforming seemingly simple questions into opportunities for deeper mathematical exploration. Remember the core concepts: simplification through the GCD, the interconvertibility of fractions, percentages, and ratios, and their widespread applicability.
Latest Posts
Latest Posts
-
Can Polygons Have Curved Sides
Sep 21, 2025
-
What Car Does Gatsby Drive
Sep 21, 2025
-
Disruptive Stabilizing And Directional Selection
Sep 21, 2025
-
Signal Detection Theory Ap Psychology
Sep 21, 2025
-
Setting Of The Giver Book
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.