What Is 10 Of 56
scising
Sep 22, 2025 · 5 min read
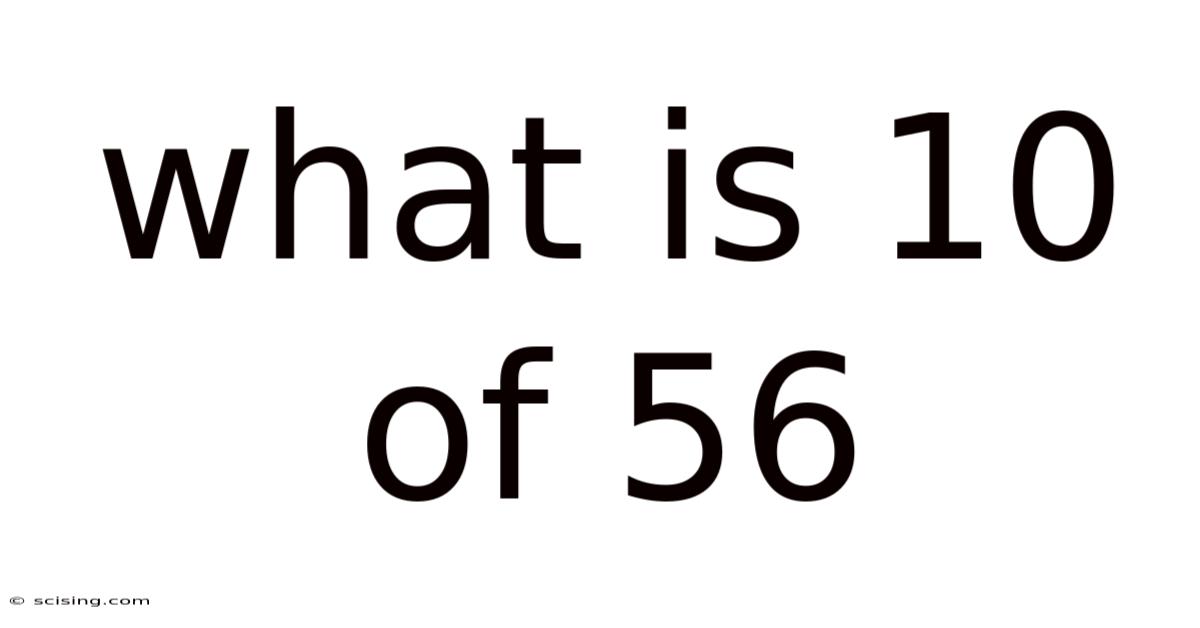
Table of Contents
What is 10% of 56? A Deep Dive into Percentages and Their Applications
Finding 10% of 56 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This article will not only show you how to calculate 10% of 56 but will also explore the broader implications of percentages, their diverse applications, and how to tackle more complex percentage problems. Understanding percentages is crucial in various aspects of life, from managing finances and understanding statistics to interpreting data in various fields.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." So, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fractional representation is key to understanding how to calculate percentages.
Calculating 10% of 56: The Simple Method
The easiest way to find 10% of any number is to divide that number by 10. Since 10% is equivalent to 1/10, dividing by 10 is the same as multiplying by 1/10 or 0.1.
Therefore, to find 10% of 56:
56 ÷ 10 = 5.6
So, 10% of 56 is 5.6
This method is incredibly efficient and works for any number. Try it with different numbers to solidify your understanding. For instance, 10% of 120 is 120 ÷ 10 = 12; 10% of 350 is 350 ÷ 10 = 35.
Calculating Percentages: A More General Approach
While the division by 10 method is perfect for 10%, we need a more general approach for other percentages. The formula to calculate X% of Y is:
(X/100) * Y
Let's apply this formula to our example:
(10/100) * 56 = 0.1 * 56 = 5.6
This confirms our earlier result. This formula is versatile and can be used to calculate any percentage of any number. For example, to find 25% of 80, you would do (25/100) * 80 = 20.
Working with Different Percentages: Examples
Let's expand our understanding by calculating other percentages of 56:
- 20% of 56: (20/100) * 56 = 11.2
- 25% of 56: (25/100) * 56 = 14
- 50% of 56: (50/100) * 56 = 28 (This is simply half of 56)
- 75% of 56: (75/100) * 56 = 42
- 100% of 56: (100/100) * 56 = 56 (This is the whole number itself)
Notice the pattern: as the percentage increases, the result increases proportionally.
Finding the Percentage: The Reverse Calculation
Sometimes, you'll need to find the percentage one number represents of another. For instance, what percentage of 80 is 20? The formula for this is:
(Part / Whole) * 100%
In our example:
(20 / 80) * 100% = 0.25 * 100% = 25%
Therefore, 20 is 25% of 80.
Real-World Applications of Percentages
Percentages are pervasive in everyday life:
-
Finance: Calculating interest rates, discounts, taxes, tips, and investment returns all rely on percentages. Understanding percentages is crucial for effective financial planning and budgeting. For example, understanding the interest rate on a loan or the APR on a credit card is essential to making informed financial decisions.
-
Retail and Sales: Discounts are often expressed as percentages (e.g., 20% off). Calculating the final price after a discount involves subtracting the percentage discount from 100% and then multiplying by the original price.
-
Statistics and Data Analysis: Percentages are used extensively to represent data and proportions. Surveys, polls, and research findings often present results as percentages to facilitate easier interpretation and comparison. For instance, understanding unemployment rates or voter turnout often involves interpreting percentages.
-
Science and Engineering: Percentages are used to express efficiency, error margins, and concentrations in various scientific and engineering calculations. For example, calculating the efficiency of a machine or the concentration of a chemical solution involves using percentages.
-
Healthcare: Percentages are used to describe disease prevalence, treatment success rates, and risk factors. Understanding the percentage chance of recovery from an illness, for instance, is vital for informed medical decisions.
Advanced Percentage Problems: Increasing and Decreasing Quantities
Percentage calculations can become more complex when dealing with increases or decreases. For instance:
-
Increasing a quantity by a percentage: If you increase a quantity by X%, you multiply the original quantity by (1 + X/100). For example, increasing 56 by 20% would be: 56 * (1 + 20/100) = 56 * 1.2 = 67.2
-
Decreasing a quantity by a percentage: If you decrease a quantity by X%, you multiply the original quantity by (1 - X/100). For example, decreasing 56 by 15% would be: 56 * (1 - 15/100) = 56 * 0.85 = 47.6
Frequently Asked Questions (FAQs)
Q1: What is the easiest way to calculate 10% of any number?
A1: The easiest way is to divide the number by 10.
Q2: Can I use a calculator to calculate percentages?
A2: Absolutely! Most calculators have a percentage function (%) which simplifies the process significantly.
Q3: What if I need to find a percentage that isn't a whole number (e.g., 7.5%)?
A3: You can still use the general formula: (X/100) * Y, replacing X with the decimal equivalent of the percentage (7.5% becomes 0.075).
Q4: How do I calculate the percentage increase or decrease between two numbers?
A4: You find the difference between the two numbers, divide the difference by the original number, and then multiply by 100% to express the result as a percentage.
Q5: Are there any online tools to help with percentage calculations?
A5: Yes, numerous online percentage calculators are available which can assist with various percentage calculations.
Conclusion: Mastering Percentages
Understanding percentages is a vital skill with far-reaching applications. While calculating 10% of 56 is a straightforward process, mastering the underlying principles allows you to tackle more complex percentage problems confidently. From managing personal finances to interpreting statistical data, proficiency in percentage calculations empowers you to navigate the numerical world with greater ease and understanding. Remember the key formulas and practice regularly to enhance your skills and build confidence in tackling percentage-related challenges. By understanding the fundamental concepts and applying the appropriate formulas, you can become adept at working with percentages in all aspects of your life.
Latest Posts
Latest Posts
-
Number Of Protons In Xenon
Sep 22, 2025
-
How Old Was Boo Radley
Sep 22, 2025
-
Difference Between Israel And Judah
Sep 22, 2025
-
Percentage 17 Out Of 20
Sep 22, 2025
-
Why Is A Tontine Illegal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.