What Is 1/8 + 1/8
scising
Sep 16, 2025 · 6 min read
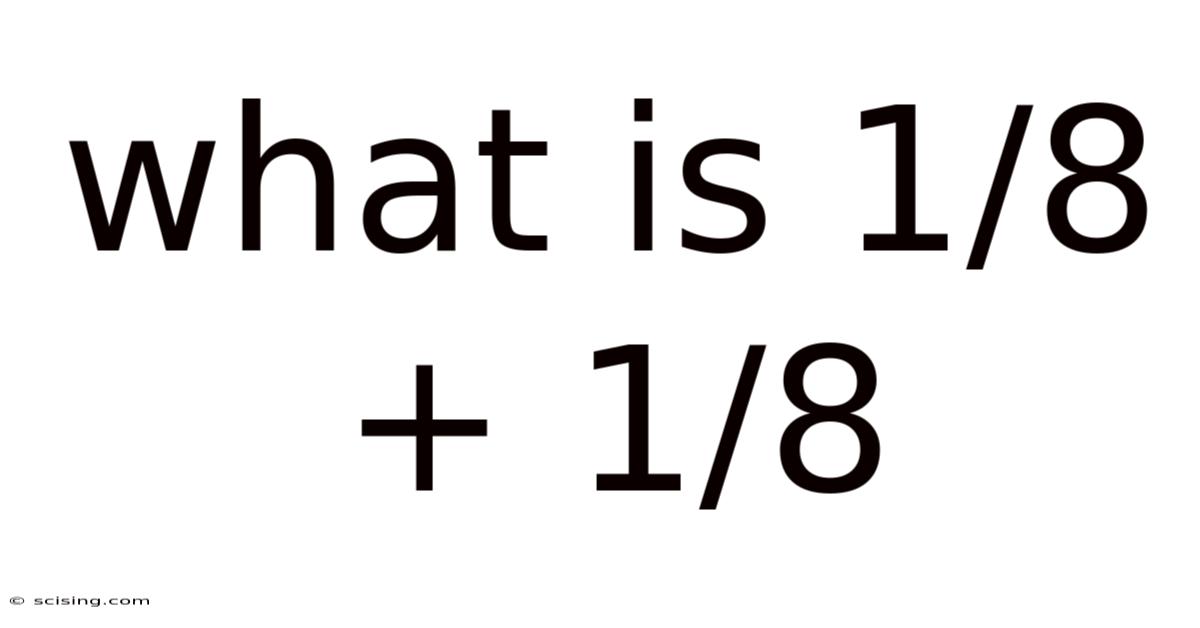
Table of Contents
Decoding the Simple Sum: What is 1/8 + 1/8? A Deep Dive into Fractions
This article delves into the seemingly simple addition problem: 1/8 + 1/8. While the answer might seem obvious at first glance, understanding the underlying principles of fraction addition provides a strong foundation for more complex mathematical concepts. We'll explore not just the solution but also the conceptual understanding behind fractions, their representation, and the methods used to add them. This guide is designed for students of all levels, from those just beginning to explore fractions to those seeking a deeper understanding of the fundamentals of arithmetic.
Understanding Fractions: Building Blocks of Mathematics
Before tackling the addition problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering.
For example, in the fraction 1/8, the denominator 8 indicates that the whole is divided into eight equal parts. The numerator 1 indicates that we are considering only one of those eight parts. Visualizing this with a pie cut into eight slices makes it clear: 1/8 represents one slice of the pie.
Fractions are fundamental to various aspects of daily life, from cooking (measuring ingredients) to construction (measuring lengths) to understanding percentages and proportions. Mastering fractions lays the groundwork for more advanced mathematical concepts, including algebra, calculus, and beyond.
Adding Fractions: A Step-by-Step Guide
Adding fractions with the same denominator is relatively straightforward. The key principle is that we are combining equal parts of the same whole. Since the denominators in 1/8 + 1/8 are the same, we can directly add the numerators while keeping the denominator constant.
Steps:
-
Check the denominators: Ensure that the denominators of the fractions are identical. In our case, both fractions have a denominator of 8.
-
Add the numerators: Add the numerators together. 1 + 1 = 2.
-
Keep the denominator the same: The denominator remains unchanged. It stays as 8.
-
Simplify the fraction (if necessary): The result of our addition is 2/8. This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 2 and 8 is 2. Dividing both the numerator and the denominator by 2 gives us the simplified fraction 1/4.
Therefore, 1/8 + 1/8 = 2/8 = 1/4.
Visual Representation: Understanding the Sum Intuitively
Visual aids can significantly enhance our understanding of fraction addition. Imagine two identical pizzas, each cut into eight equal slices. The fraction 1/8 represents one slice from each pizza. If you take one slice from the first pizza (1/8) and another slice from the second pizza (1/8), you now have two slices. Since each pizza was divided into eight slices, you have 2 out of 8 slices, or 2/8. This simplifies to 1/4, representing one slice from a pizza cut into four equal pieces. This visual representation clearly demonstrates the addition and simplification process.
Adding Fractions with Different Denominators
While our example involves fractions with the same denominator, adding fractions with different denominators requires an extra step: finding a common denominator. A common denominator is a number that is a multiple of both denominators.
For example, let's add 1/3 + 1/4. The least common multiple (LCM) of 3 and 4 is 12. We need to convert both fractions to have a denominator of 12:
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 1/4 = (1 x 3) / (4 x 3) = 3/12
Now we can add the fractions: 4/12 + 3/12 = 7/12.
The Importance of Simplifying Fractions
Simplifying fractions, also known as reducing fractions to their lowest terms, is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret. 1/4 is clearer than 2/8.
- Consistency: Simplifying fractions ensures consistent representation of the same value.
- Efficiency: Simplified fractions make calculations simpler in more complex problems.
Real-World Applications: Fractions in Everyday Life
Fractions are not just abstract mathematical concepts; they have numerous applications in everyday life:
- Cooking and Baking: Recipes often require fractional measurements of ingredients (e.g., 1/2 cup of flour, 1/4 teaspoon of salt).
- Measurement: Measuring lengths, weights, and volumes often involves fractions (e.g., 1/8 inch, 1/2 kilometer).
- Finance: Understanding percentages and proportions, which are fundamentally based on fractions, is crucial for managing personal finances.
- Time Management: Dividing time into fractions (e.g., 1/4 of an hour, 1/2 a day) helps us schedule and organize our activities.
Beyond the Basics: Extending Fraction Knowledge
Understanding the addition of simple fractions like 1/8 + 1/8 provides a solid foundation for tackling more complex fraction operations, including:
- Subtraction of Fractions: Similar principles apply to subtracting fractions, with the focus on finding a common denominator and subtracting numerators.
- Multiplication of Fractions: Multiplying fractions involves multiplying the numerators and denominators separately.
- Division of Fractions: Dividing fractions involves inverting the second fraction and then multiplying.
- Mixed Numbers: Mixed numbers combine whole numbers and fractions (e.g., 1 1/2). Adding, subtracting, multiplying, and dividing mixed numbers requires understanding the conversion between mixed numbers and improper fractions.
Frequently Asked Questions (FAQ)
Q: Why is it important to find a common denominator when adding fractions with different denominators?
A: Finding a common denominator allows us to add or subtract parts of the same whole. We cannot directly add or subtract parts of different sizes without first converting them to a common unit of measurement.
Q: How do I find the greatest common divisor (GCD)?
A: The GCD is the largest number that divides evenly into both the numerator and the denominator. Several methods exist, including listing factors and using the Euclidean algorithm.
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4).
Q: How do I convert an improper fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same.
Conclusion: Mastering Fractions – A Journey Worth Taking
The seemingly simple problem of 1/8 + 1/8 opens the door to a deeper understanding of fractions and their essential role in mathematics and daily life. By mastering the fundamentals of fraction addition, you build a strong foundation for tackling more advanced mathematical concepts and successfully applying these skills to various real-world situations. Remember, the key is not just memorizing the steps but also understanding the underlying principles and visual representations to solidify your grasp of these fundamental building blocks of mathematics. Continue exploring and practicing, and you will find that your confidence and skills in handling fractions will steadily grow.
Latest Posts
Latest Posts
-
How To Find Zeros Algebraically
Sep 16, 2025
-
Molar Mass Ni No3 2
Sep 16, 2025
-
How Long Is 600 Meters
Sep 16, 2025
-
20 Dollars 30 Percent Off
Sep 16, 2025
-
Black Ships Before Troy Notes
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/8 + 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.