Ten Percent Of A Million
scising
Sep 22, 2025 · 5 min read
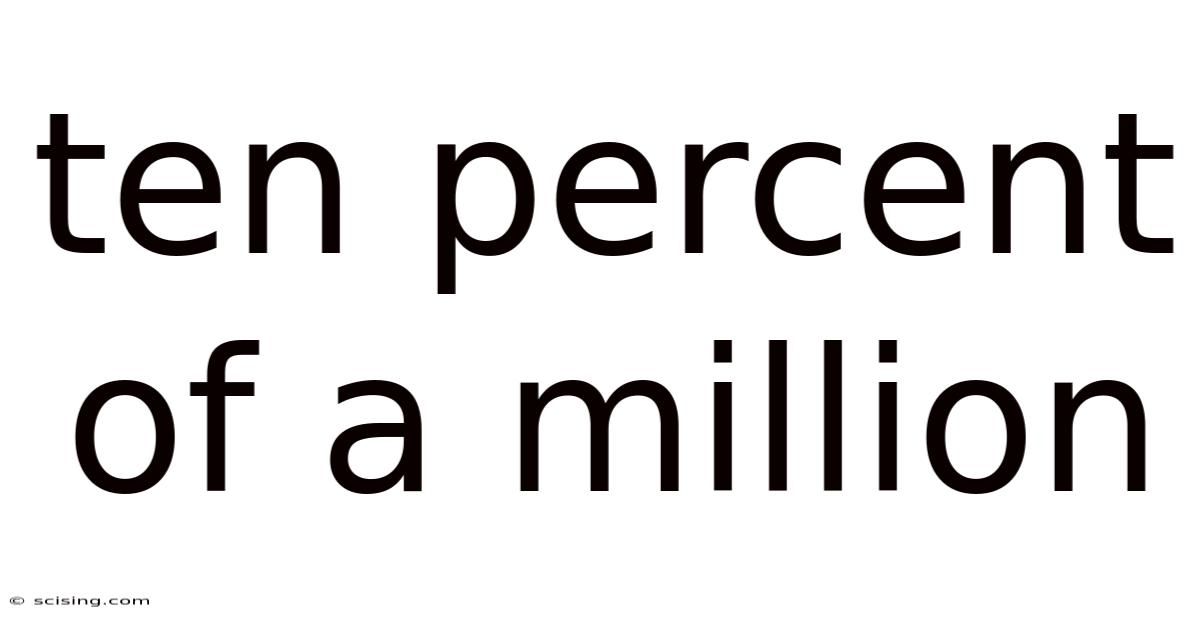
Table of Contents
Ten Percent of a Million: Understanding Percentages and Large Numbers
Have you ever wondered what ten percent of a million is? This seemingly simple question delves into fundamental concepts of percentages and large numbers, crucial for everyday life, from budgeting and savings to understanding financial news and making informed business decisions. This article will not only answer the question directly but also explore the underlying mathematical principles and practical applications of calculating percentages, especially when dealing with substantial amounts. We will also tackle common misconceptions and offer helpful strategies for handling similar calculations.
Understanding Percentages
Before diving into the calculation of ten percent of a million, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
To calculate a percentage of a number, we typically follow these steps:
- Convert the percentage to a decimal: Divide the percentage by 100. For example, 10% becomes 0.10 (or simply 0.1).
- Multiply the decimal by the number: This gives you the required percentage of the number.
Let's illustrate with a smaller example: What is 25% of 80?
- 25% / 100 = 0.25
- 0.25 * 80 = 20
Therefore, 25% of 80 is 20.
Calculating Ten Percent of a Million
Now, let's tackle the main question: What is 10% of 1,000,000?
Using the steps outlined above:
- Convert the percentage to a decimal: 10% / 100 = 0.1
- Multiply the decimal by the number: 0.1 * 1,000,000 = 100,000
Therefore, 10% of 1,000,000 is 100,000.
Practical Applications: Real-World Examples
Understanding how to calculate percentages, especially with larger numbers like a million, has numerous practical applications:
- Finance and Investments: Calculating returns on investment, understanding interest rates, analyzing financial statements, and determining the value of stocks often involve percentage calculations. For instance, if you invest $1,000,000 and receive a 10% return, you've earned $100,000.
- Sales and Marketing: Businesses use percentages to calculate discounts, markups, sales tax, and profit margins. A 10% discount on a $1,000,000 property would be a significant $100,000 reduction.
- Budgeting and Personal Finance: Tracking expenses, saving for retirement, and managing personal finances all require understanding and applying percentages. If you aim to save 10% of your $1,000,000 annual income, you would save $100,000.
- Data Analysis and Statistics: Percentages are fundamental in data analysis for representing proportions, trends, and changes in data sets. Understanding the percentage change in sales figures, population growth, or market share relies heavily on these calculations.
- Real Estate: Calculating property taxes, down payments, and appreciation often involves working with percentages of large sums. A 10% down payment on a $1,000,000 house would amount to $100,000.
Beyond the Basics: More Complex Percentage Calculations
While calculating 10% of a million is relatively straightforward, real-world scenarios might involve more complex percentage calculations:
- Calculating multiple percentages: Imagine a scenario where you need to calculate a 5% commission on a $1,000,000 sale, followed by a 2% tax on the commission. This would involve two separate percentage calculations.
- Calculating percentage increases or decreases: Understanding percentage changes is crucial for tracking growth or decline in various aspects of life. For instance, if a $1,000,000 investment increased by 15%, the new value would be $1,150,000. Conversely, a 10% decrease would result in a value of $900,000.
- Working with compound interest: Compound interest is the interest earned on both the principal amount and accumulated interest. It is a more complex calculation that involves repeatedly applying a percentage over time. It is particularly relevant in long-term investments.
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations, leading to errors in various contexts:
- Adding percentages directly: You cannot simply add percentages directly unless they are applied to the same base amount. For example, a 10% increase followed by a 10% decrease does not result in the original amount.
- Confusing percentage change with absolute change: Percentage change indicates the relative change compared to the original value, while absolute change shows the actual difference in numerical terms.
- Incorrect rounding: Improper rounding of percentages during intermediate steps can lead to significant inaccuracies in the final result.
Tips and Tricks for Calculating Percentages
Several techniques can simplify percentage calculations:
- Using a calculator: Calculators are essential tools for quickly and accurately computing percentages, especially with large numbers.
- Mental math shortcuts: For simpler percentages (like 10%, 25%, 50%), mental math shortcuts can be employed. For example, 10% is easily calculated by dividing by 10.
- Using fractions: Converting percentages to equivalent fractions can sometimes simplify calculations, particularly when dealing with common fractions like 1/4 (25%), 1/2 (50%), or 3/4 (75%).
- Breaking down complex calculations: Break down complex calculations into smaller, manageable steps. This reduces errors and enhances understanding.
Frequently Asked Questions (FAQ)
- Q: How do I calculate a percentage increase? A: Subtract the original value from the new value, divide the result by the original value, and multiply by 100.
- Q: How do I calculate a percentage decrease? A: Subtract the new value from the original value, divide the result by the original value, and multiply by 100.
- Q: What if the percentage is more than 100%? A: This simply means the final value is more than double the original value.
- Q: How can I improve my understanding of percentages? A: Practice regularly with different examples and work through various problem-solving scenarios.
Conclusion
Understanding how to calculate ten percent of a million, and percentages in general, is a fundamental skill with widespread applications in various aspects of life. From personal finance to business decisions and data analysis, the ability to accurately calculate percentages empowers individuals to make informed choices and solve problems efficiently. Mastering percentage calculations requires a strong grasp of mathematical principles, attention to detail, and consistent practice. By overcoming common misconceptions and employing helpful techniques, individuals can confidently navigate the world of percentages and large numbers. Remember, the ability to handle these calculations is not merely a mathematical skill but a crucial life skill that enhances financial literacy and problem-solving abilities.
Latest Posts
Latest Posts
-
Convert 64 Oz To Liters
Sep 22, 2025
-
750 Grams How Many Pounds
Sep 22, 2025
-
For You In French Language
Sep 22, 2025
-
Lewis Dot Structure For Scl4
Sep 22, 2025
-
Ounces In A Pound Chart
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Ten Percent Of A Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.