Square Root Of Negative 2
scising
Sep 10, 2025 · 6 min read
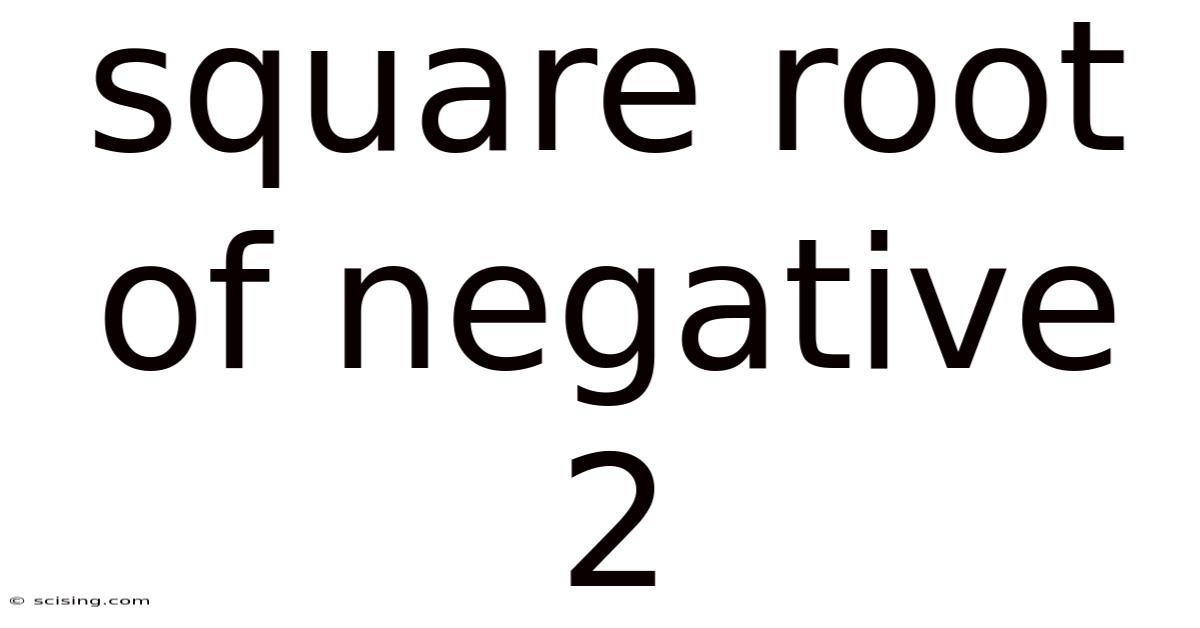
Table of Contents
Delving into the Depths: Understanding the Square Root of Negative Two
The square root of negative two, denoted as √(-2), might seem like a mathematical enigma at first glance. After all, how can you find a number that, when multiplied by itself, results in a negative value? Our everyday experience with numbers focuses on positive values and their squares, leading to a natural assumption that the square root of a negative number is impossible. However, this seemingly simple question opens the door to a fascinating realm of mathematics: the realm of complex numbers. This article will explore the concept of √(-2), explain its representation, its properties, and some of its applications, demystifying this seemingly paradoxical entity.
Introduction to Complex Numbers: Beyond Real Numbers
Before we delve into the specifics of √(-2), we need to expand our understanding beyond the familiar realm of real numbers. Real numbers encompass all the numbers you've likely encountered so far – positive and negative whole numbers (integers), fractions (rational numbers), and even numbers like π (irrational numbers). These numbers can be plotted on a single number line.
However, the square root of a negative number cannot be represented on this line. This is where complex numbers come in. A complex number is a number that can be expressed in the form a + bi, where:
ais the real part of the complex number.bis the imaginary part of the complex number.iis the imaginary unit, defined as √(-1).
The imaginary unit, i, is the keystone to understanding complex numbers. It's a number whose square is -1 (i² = -1). This seemingly simple definition unlocks a whole new dimension in mathematics, allowing us to solve equations previously deemed unsolvable within the real number system.
Calculating √(-2): Introducing the Imaginary Unit
Now, let's return to our original question: what is √(-2)? Using the properties of complex numbers, we can rewrite this as follows:
√(-2) = √(2 * -1) = √(2) * √(-1)
Since √(-1) is defined as i, we can express √(-2) as:
√(-2) = √(2)i
Therefore, the square root of negative two is √2 * i. This is a complex number with a real part of 0 and an imaginary part of √2. It cannot be represented on the real number line but exists in the complex plane.
Visualizing Complex Numbers: The Complex Plane
To better understand complex numbers, it's helpful to visualize them using the complex plane. This is a two-dimensional plane where the horizontal axis represents the real part of the complex number and the vertical axis represents the imaginary part. The complex number a + bi is represented by the point (a, b) on this plane.
√(-2), or √2 * i, is represented by the point (0, √2) on the complex plane. This point lies on the positive imaginary axis, a distance of √2 units from the origin.
Properties of √(-2) and its Operations
Like all complex numbers, √(-2) has several important properties:
-
Addition and Subtraction: Complex numbers are added and subtracted by adding or subtracting their real and imaginary parts separately. For example, adding √(-2) to 2 + 3i would result in 2 + (3 + √2)i.
-
Multiplication: Multiplication involves using the distributive property and remembering that i² = -1. For example, multiplying √(-2) by 2i would be: (√2 * i) * (2i) = 2√2 * i² = -2√2
-
Division: Division involves multiplying both the numerator and the denominator by the complex conjugate of the denominator. The complex conjugate of a complex number a + bi is a - bi.
-
Magnitude (Modulus): The magnitude (or modulus) of a complex number represents its distance from the origin in the complex plane. The magnitude of √(-2) is calculated as |√(-2)| = √(0² + (√2)²) = √2.
-
Argument: The argument of a complex number is the angle it makes with the positive real axis in the complex plane. The argument of √(-2) is π/2 radians (or 90 degrees).
Applications of Complex Numbers: Beyond the Theoretical
While √(-2) might seem like an abstract mathematical concept, complex numbers have far-reaching applications across various fields:
-
Electrical Engineering: Complex numbers are essential for analyzing alternating current (AC) circuits. They allow engineers to represent voltage, current, and impedance in a way that simplifies calculations and makes circuit analysis more manageable.
-
Quantum Mechanics: Complex numbers play a fundamental role in quantum mechanics, where wave functions are often described using complex numbers. These functions are used to predict the behavior of particles at the subatomic level.
-
Signal Processing: Complex numbers are instrumental in analyzing and manipulating signals. Techniques like the Fourier transform rely heavily on complex numbers to decompose signals into their constituent frequencies.
-
Fluid Dynamics: Complex analysis techniques are used to model and solve complex problems in fluid flow and aerodynamics.
-
Fractals and Chaos Theory: Complex numbers are central to the creation and study of fractals, beautiful and complex geometric shapes generated by iterative processes.
Frequently Asked Questions (FAQ)
Q1: Can I simplify √(-2) further?
A1: While you can express it as √2 * i, there's no simpler algebraic form. The expression √2 * i accurately represents the square root of -2 in the complex number system.
Q2: What is the difference between √(-2) and -√(-2)?
A2: √(-2) and -√(-2) are distinct complex numbers. They both have the same magnitude (√2), but they have different arguments. √(-2) has an argument of π/2, while -√(-2) has an argument of 3π/2. They are reflections of each other across the real axis in the complex plane.
Q3: Are there other square roots of -2?
A3: No, there are only two square roots of -2, namely √2 * i and -√2 * i. This is true for any complex number; each has two square roots which are negations of each other.
Q4: Why are complex numbers important?
A4: Complex numbers provide a mathematically consistent framework for dealing with situations that are impossible to handle solely within the system of real numbers. They are indispensable in numerous fields, offering powerful tools for solving complex problems and gaining insights into phenomena that would otherwise be incomprehensible.
Conclusion: Embracing the Complexity
The square root of negative two, seemingly a simple concept, leads us into the fascinating world of complex numbers. While it might initially seem counterintuitive to think about the square root of a negative number, the introduction of the imaginary unit i opens up a whole new realm of mathematical possibilities. Complex numbers have proven invaluable in various scientific and engineering fields, demonstrating that delving into the seemingly paradoxical can unveil profound and practical applications. The journey into understanding √(-2) is not just about solving a mathematical problem; it’s about expanding our understanding of numbers and their power to model the complexities of our world. So embrace the complexity – it’s often where the most exciting discoveries lie.
Latest Posts
Latest Posts
-
Nitrogen Filled Tires Near Me
Sep 10, 2025
-
What Day Is Feb 28
Sep 10, 2025
-
Male Or Female In Spanish
Sep 10, 2025
-
What Is Realistic Fiction Genre
Sep 10, 2025
-
How Long Is 37 Inches
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of Negative 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.