Square Root Of 1 9
scising
Sep 12, 2025 · 5 min read
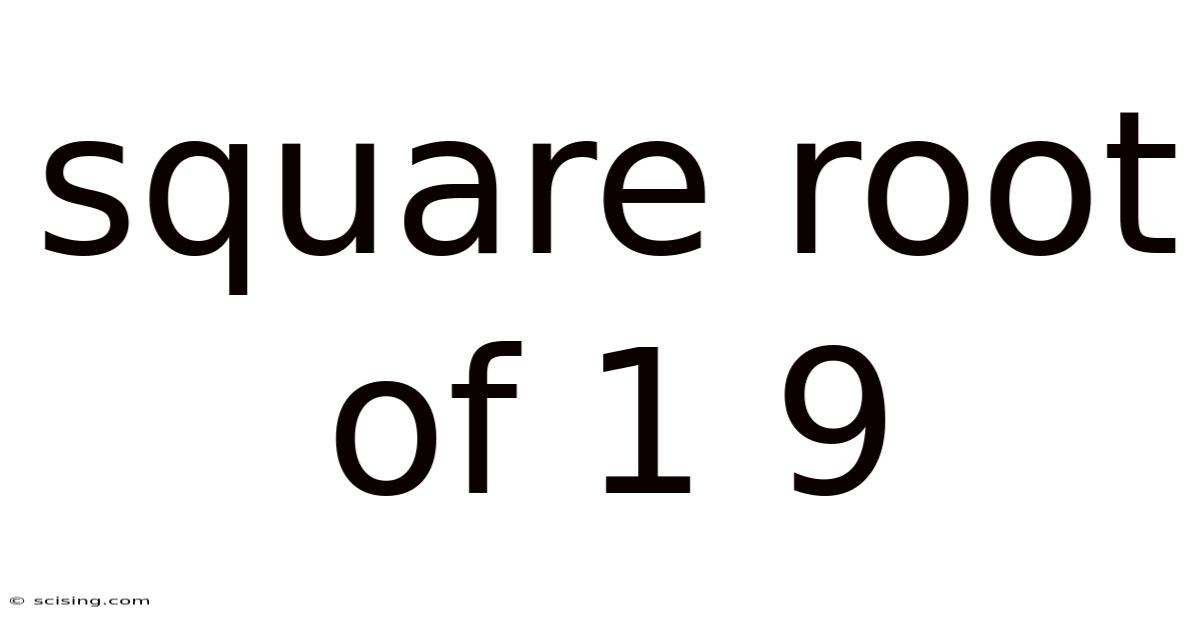
Table of Contents
Understanding the Square Root of 19: A Deep Dive into Irrational Numbers
The square root of 19, denoted as √19, is a fascinating mathematical concept that introduces us to the world of irrational numbers. This article will explore this seemingly simple number in depth, examining its properties, calculation methods, and its significance within the broader field of mathematics. We'll delve into how to approximate its value, discuss its irrationality, and explore its applications in various contexts. Understanding √19 helps solidify our grasp of fundamental mathematical principles and lays the groundwork for more advanced concepts.
What is a Square Root?
Before diving into the specifics of √19, let's refresh our understanding of square roots. The square root of a number x is a value that, when multiplied by itself, equals x. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9.
Why is √19 Special?
Unlike the square root of 9, which yields a whole number, the square root of 19 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, meaning it goes on forever without ever settling into a repeating pattern. This is a key characteristic that distinguishes it from rational numbers like √9 or √16.
Calculating √19: Methods and Approximations
Since √19 is irrational, we cannot find its exact decimal value. However, we can use several methods to approximate its value:
1. Babylonian Method (or Heron's Method): This iterative method refines an initial guess to get progressively closer to the actual value. The formula is:
x_(n+1) = 0.5 * (x_n + 19/x_n)
Where:
- x_n is the current approximation.
- x_(n+1) is the next, improved approximation.
Let's start with an initial guess of x_0 = 4 (because 4² = 16, which is close to 19):
- x_1 = 0.5 * (4 + 19/4) = 4.25
- x_2 = 0.5 * (4.25 + 19/4.25) ≈ 4.3588
- x_3 = 0.5 * (4.3588 + 19/4.3588) ≈ 4.3589
As you can see, the value converges quickly. After a few iterations, we get a reasonably accurate approximation of √19.
2. Using a Calculator: Most scientific calculators have a square root function (√) that provides a highly accurate decimal approximation. Using a calculator, we find that √19 ≈ 4.35889894354.
3. Linear Approximation: This method uses the tangent line to the graph of y = √x at a nearby point to estimate the value. While less precise than the Babylonian method, it’s conceptually simpler.
4. Numerical Methods: More advanced numerical methods, such as the Newton-Raphson method, can provide even more accurate approximations. These methods are typically used in computer programs for high-precision calculations.
Understanding Irrationality: Why √19 is Not a Fraction
The proof that √19 is irrational involves a technique called proof by contradiction. We assume that √19 is rational, meaning it can be expressed as a fraction a/b, where 'a' and 'b' are integers, and the fraction is in its simplest form (meaning 'a' and 'b' share no common factors other than 1).
If √19 = a/b, then squaring both sides gives:
19 = a²/b²
Rearranging, we get:
19b² = a²
This equation tells us that a² is a multiple of 19. Since 19 is a prime number, this implies that 'a' itself must also be a multiple of 19. We can write 'a' as 19k, where 'k' is another integer.
Substituting this into the equation above:
19b² = (19k)² = 361k²
Dividing both sides by 19:
b² = 19k²
This shows that b² is also a multiple of 19, and therefore 'b' must be a multiple of 19 as well.
But this contradicts our initial assumption that a/b is in its simplest form. Both 'a' and 'b' are multiples of 19, meaning they share a common factor. This contradiction proves our initial assumption must be false, therefore √19 is irrational. This proof technique can be generalized to prove the irrationality of the square root of any non-perfect square.
Applications of √19
While √19 might seem like an abstract mathematical concept, it has practical applications in various fields:
-
Geometry: √19 could represent the length of the diagonal of a rectangle or the hypotenuse of a right-angled triangle with specific side lengths. In geometry problems involving Pythagorean theorem calculations, irrational numbers like √19 frequently arise.
-
Physics: Many physical phenomena involve irrational numbers in their mathematical descriptions. For example, calculations involving vectors, oscillations, or wave propagation could lead to expressions that include √19.
-
Engineering: Similar to physics, engineering applications often use irrational numbers in calculations related to structures, circuits, or signal processing.
-
Computer Science: Approximating irrational numbers like √19 is crucial in computer graphics and simulations where high precision is needed. Algorithms for efficient approximation are essential for rendering realistic images and simulations.
Frequently Asked Questions (FAQ)
Q1: Is there an exact value for √19?
A1: No, there isn't an exact decimal value for √19. Its decimal representation is non-terminating and non-repeating, making it an irrational number. We can only approximate its value.
Q2: How can I calculate √19 without a calculator?
A2: You can use the Babylonian method (Heron's method) or linear approximation to manually calculate an approximation. The Babylonian method offers better accuracy with fewer iterations.
Q3: What is the difference between rational and irrational numbers?
A3: Rational numbers can be expressed as a ratio of two integers (a fraction), while irrational numbers cannot. Rational numbers have either terminating or repeating decimal representations, whereas irrational numbers have non-terminating, non-repeating decimal representations.
Q4: What are some other examples of irrational numbers?
A4: Besides √19, other famous irrational numbers include π (pi), e (Euler's number), and the golden ratio (φ).
Conclusion
The square root of 19, while seemingly simple, exemplifies the beauty and complexity of mathematics. Its irrationality highlights the vastness of numbers beyond the familiar realm of rational numbers. Understanding its properties, calculation methods, and applications underscores the importance of fundamental mathematical concepts and their relevance in various fields. Whether you’re a student grappling with these concepts or a curious individual fascinated by mathematics, understanding √19 provides a deeper appreciation for the intricacies of numbers and their role in the world around us. The journey of understanding irrational numbers like √19 is a rewarding one, deepening our understanding of the mathematical landscape and encouraging further exploration.
Latest Posts
Latest Posts
-
How To Determine Square Yards
Sep 12, 2025
-
Food Chain Of The Taiga
Sep 12, 2025
-
Car Gar Zar Verbs Spanish
Sep 12, 2025
-
Is Sugar Polar Or Nonpolar
Sep 12, 2025
-
Does A Duck Have Ears
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.