Sin 2 Cos 2 1
scising
Sep 09, 2025 · 6 min read
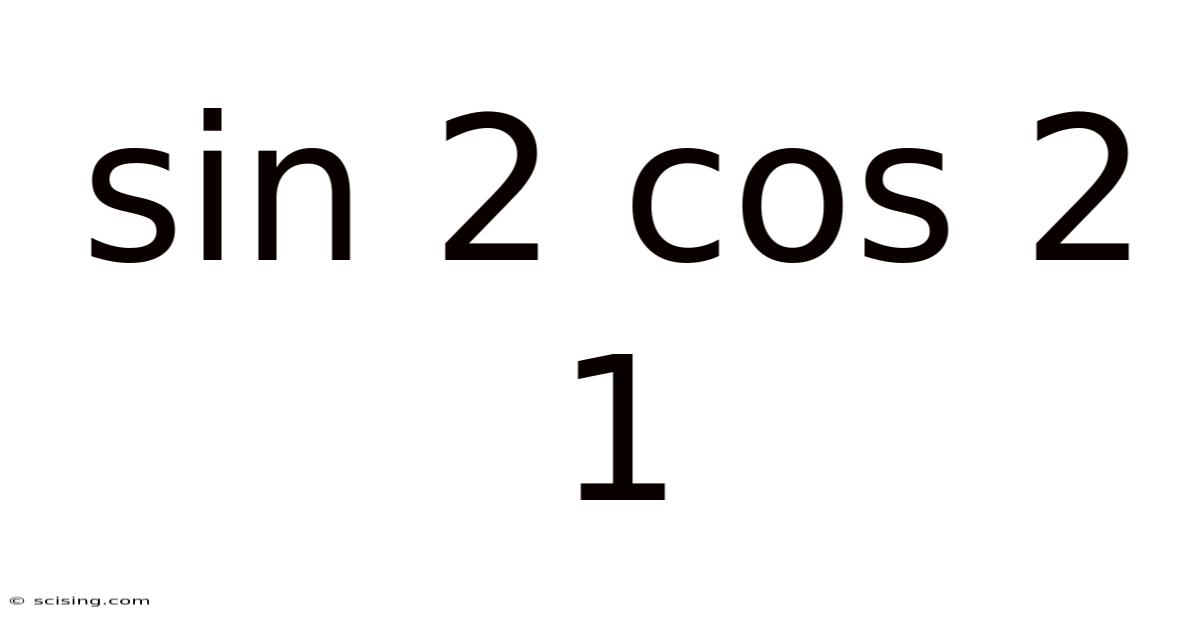
Table of Contents
Unraveling the Trigonometric Identity: sin²x, cos²x, and the Fundamental Relationship
This article delves into the fascinating world of trigonometry, focusing on the fundamental relationship between sin²x and cos²x, and how understanding this relationship unlocks a deeper comprehension of trigonometric identities and their applications. We'll explore the core identity, its derivations, practical applications, and answer frequently asked questions to solidify your understanding. Understanding sin²x, cos²x, and their interplay is crucial for anyone studying mathematics, physics, engineering, or computer graphics.
Introduction: The Pythagorean Trigonometric Identity
The cornerstone of this exploration is the Pythagorean trigonometric identity: sin²x + cos²x = 1. This isn't just a random equation; it's a direct consequence of the Pythagorean theorem applied to a unit circle. Imagine a right-angled triangle inscribed within a unit circle (a circle with a radius of 1). The hypotenuse of this triangle is the radius of the circle (which is 1), and the lengths of the other two sides correspond to sin x and cos x. The Pythagorean theorem (a² + b² = c²) then translates directly into sin²x + cos²x = 1².
This seemingly simple equation is surprisingly powerful. It's the foundation for deriving numerous other trigonometric identities and simplifying complex expressions. Its applications extend far beyond the theoretical realm, playing a crucial role in solving real-world problems in various fields.
Derivation of the Pythagorean Identity
Let's visualize the derivation. Consider a point P(x, y) on a unit circle centered at the origin (0, 0). The angle formed between the positive x-axis and the line segment connecting the origin to point P is denoted by x.
- Cosine: The x-coordinate of point P represents the cosine of angle x: x = cos x.
- Sine: The y-coordinate of point P represents the sine of angle x: y = sin x.
According to the equation of a circle, the coordinates (x, y) satisfy the equation x² + y² = r², where r is the radius. Since we're working with a unit circle (r = 1), this simplifies to:
x² + y² = 1
Substituting the trigonometric definitions of x and y, we arrive at the Pythagorean identity:
cos²x + sin²x = 1
Alternative Derivations and Perspectives:
While the unit circle approach is intuitive, the Pythagorean identity can also be derived using other methods. One approach involves considering the definitions of sine and cosine in terms of the sides of a right-angled triangle:
- sin x = opposite side / hypotenuse
- cos x = adjacent side / hypotenuse
By applying the Pythagorean theorem (opposite² + adjacent² = hypotenuse²) and substituting these definitions, we again arrive at sin²x + cos²x = 1.
This reinforces the fundamental geometric nature of this identity and its connection to the most basic principles of trigonometry.
Manipulating the Identity: Deriving other useful identities
The beauty of sin²x + cos²x = 1 lies in its versatility. We can rearrange it to derive several other important identities:
-
Solving for sin²x:
sin²x = 1 - cos²x
This is useful when we need to express sin²x in terms of cos²x, and vice-versa.
-
Solving for cos²x:
cos²x = 1 - sin²x
Similarly, this allows us to express cos²x in terms of sin²x.
-
Expressing in terms of tangent:
Dividing the original identity by cos²x gives:
tan²x + 1 = sec²x
This identity is crucial when dealing with tangent and secant functions.
-
Expressing in terms of cotangent:
Dividing the original identity by sin²x gives:
cot²x + 1 = csc²x
This provides a similar relationship for cotangent and cosecant.
Applications of sin²x and cos²x
The applications of sin²x and cos²x are vast and span many fields:
-
Physics: These identities are fundamental in describing oscillatory motion (like simple harmonic motion of a pendulum) and wave phenomena (sound, light). The power and energy in waves are often expressed using these functions.
-
Engineering: In electrical engineering, AC circuit analysis heavily relies on these trigonometric functions. Understanding the phase relationships between voltage and current involves manipulating these identities. Civil and structural engineering also employs them in analyzing stress and strain under dynamic loading conditions.
-
Computer Graphics: Creating realistic simulations of light and shadow in computer graphics often utilizes trigonometric functions, including sine and cosine, to accurately model reflections and refractions.
-
Calculus: Derivatives and integrals involving trigonometric functions frequently utilize these identities for simplification and solving complex problems.
Solving Trigonometric Equations
The Pythagorean identity is essential for solving trigonometric equations. Many equations can be simplified and reduced to a solvable form by using this identity to substitute one function in terms of another. For example:
Let's say we have the equation: 2sin²x + cos²x = 1. We can use the identity cos²x = 1 - sin²x to rewrite the equation as:
2sin²x + (1 - sin²x) = 1
This simplifies to sin²x = 0, which implies sin x = 0. This then allows us to find the solutions for x.
Frequently Asked Questions (FAQs)
-
Q: What is the difference between sin x and sin²x?
- A: sin x represents the sine of angle x, while sin²x represents (sin x)², or the square of the sine of angle x. They are different functions with different properties and values.
-
Q: Can sin²x + cos²x = 1 be used for any angle x?
- A: Yes, this identity holds true for all angles x, whether they are acute, obtuse, or even negative.
-
Q: Are there any limitations to the Pythagorean identity?
- A: The identity itself is universally true. However, when solving equations using this identity, one must consider the possible ranges of solutions for sine and cosine, accounting for multiple solutions within a given period.
-
Q: How do I remember the Pythagorean identity?
- A: Visualize the unit circle. Or, think of it as a direct translation of the Pythagorean theorem applied to a right-angled triangle within a unit circle. Repetition and practice will help commit it to memory.
-
Q: How can I further improve my understanding of trigonometric identities?
- A: Practice solving a variety of trigonometric equations and problems. Work through examples and try to derive other identities using the Pythagorean identity as a starting point. Consult textbooks and online resources for further explanation and practice problems.
Conclusion:
The trigonometric identity sin²x + cos²x = 1 is far more than a simple equation; it's a fundamental principle with profound implications across various disciplines. Understanding its derivation, manipulation, and applications is paramount for mastering trigonometry and appreciating its role in solving real-world problems. By comprehending this core identity, you unlock a gateway to a deeper understanding of the elegant and powerful world of mathematics and its applications in science and technology. Remember, consistent practice and a curious mind are key to mastering trigonometric identities and unlocking their full potential. The journey into the intricacies of sin²x, cos²x, and their relationship with the number 1 is both intellectually rewarding and practically invaluable.
Latest Posts
Latest Posts
-
What Was The Black Legend
Sep 10, 2025
-
Sensory Interaction Ap Psychology Definition
Sep 10, 2025
-
Images From Romeo And Juliet
Sep 10, 2025
-
How Much Is 90 Oz
Sep 10, 2025
-
Is Melting Ice Chemical Change
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Sin 2 Cos 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.