One Half Plus One Half
scising
Sep 24, 2025 · 5 min read
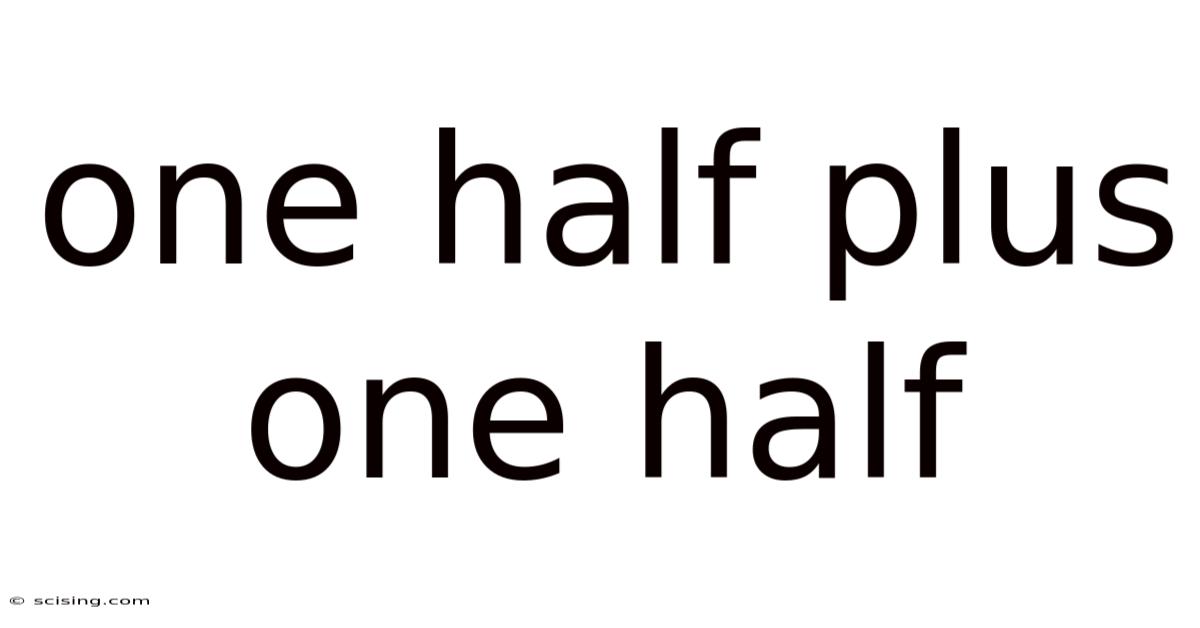
Table of Contents
One Half Plus One Half: A Deep Dive into Fractions and Their Applications
What happens when you add one half and one half? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics with far-reaching applications in everyday life and advanced fields. This article will explore the addition of one half and one half, not just as a simple arithmetic problem, but as a gateway to grasping the broader principles of fractions, their representation, and their use in various contexts. We'll delve into the underlying principles, explore different methods of solving the problem, and consider the practical implications of this seemingly basic concept.
Understanding Fractions: The Building Blocks
Before tackling the problem of one half plus one half, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering.
For example, in the fraction ½ (one half), the denominator (2) signifies that the whole is divided into two equal parts, and the numerator (1) represents one of those parts. Similarly, ¾ (three quarters) means the whole is divided into four equal parts, and we're considering three of them.
Understanding fractions is crucial not only for basic arithmetic but also for more advanced mathematical concepts like algebra, calculus, and even probability and statistics. They form the basis for understanding ratios, proportions, and percentages – all vital tools in numerous fields.
Adding One Half and One Half: A Step-by-Step Approach
Now, let's tackle the central question: what is ½ + ½?
There are several ways to solve this, each illustrating different aspects of fraction manipulation.
Method 1: Visual Representation
Imagine you have a pizza cut into two equal slices. One half (½) represents one slice. If you add another half (½), you now have two slices out of the two total slices. This visually demonstrates that ½ + ½ = 1 (one whole pizza).
Method 2: Common Denominators
This method is crucial for adding fractions with different denominators. Since both fractions in our problem have the same denominator (2), adding them is straightforward. We simply add the numerators and keep the common denominator:
1/2 + 1/2 = (1 + 1) / 2 = 2/2 = 1
This reinforces the idea that two halves make a whole.
Method 3: Decimal Conversion
Fractions can also be represented as decimals. One half (½) is equivalent to 0.5 (as 1 divided by 2 is 0.5). Therefore:
0.5 + 0.5 = 1.0 = 1
This method provides an alternative perspective, demonstrating the equivalence between fractions and decimals.
Beyond the Basics: Exploring More Complex Fraction Addition
While adding ½ + ½ is relatively simple, understanding the principles involved allows us to tackle more complex fraction addition problems. Let's consider adding fractions with different denominators:
For example, let's add ¼ + ⅓. We cannot simply add the numerators and denominators. Instead, we need to find a common denominator, which is the least common multiple (LCM) of the denominators. In this case, the LCM of 4 and 3 is 12. We then rewrite the fractions with the common denominator:
¼ = 3/12 (multiplying numerator and denominator by 3) ⅓ = 4/12 (multiplying numerator and denominator by 4)
Now we can add:
3/12 + 4/12 = (3 + 4) / 12 = 7/12
Real-World Applications of Fraction Addition
The seemingly simple addition of fractions has wide-ranging practical applications:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions is essential to accurately measure and combine ingredients. For example, a recipe might call for ½ cup of sugar and ½ cup of flour. Understanding fraction addition helps determine the total amount of dry ingredients needed.
-
Measurement and Construction: In construction and engineering, precise measurements are critical. Fractions are used extensively to represent lengths, widths, and other dimensions. Adding fractions is essential for calculating total lengths or areas.
-
Finance and Budgeting: Managing personal finances often involves working with fractions of money. For example, understanding how much of your budget is allocated to different expenses requires adding fractions representing budget portions.
-
Data Analysis and Statistics: Fractions and their manipulation are fundamental to data analysis and statistics. Representing proportions, calculating averages, and interpreting statistical data all involve working with fractions.
-
Time Management: Dividing time into fractional parts is common in scheduling and time management. For example, adding up the time spent on different tasks involves fraction addition if the time units are expressed as fractions of an hour or other time unit.
Frequently Asked Questions (FAQ)
Q: What if I have more than two fractions to add?
A: The process remains similar. If the fractions share a common denominator, add the numerators and keep the common denominator. If not, find the least common multiple (LCM) of the denominators, rewrite the fractions with the common denominator, and then add the numerators.
Q: Can I add fractions and whole numbers together?
A: Yes. Rewrite the whole number as a fraction with a denominator of 1. For example, to add 2 + ½, rewrite 2 as 2/1. Then find a common denominator (in this case, 2) and add: 4/2 + 1/2 = 5/2 or 2 ½.
Q: What happens if the result of adding fractions is an improper fraction (numerator is larger than the denominator)?
A: An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction. For example, 5/2 can be simplified to 2 ½.
Conclusion: The Significance of a Simple Sum
The seemingly simple addition of one half and one half, resulting in one whole, is more than just a basic arithmetic problem. It's a foundational concept in mathematics that underscores the principles of fractions, their representation, and their applications in numerous real-world scenarios. Mastering fraction addition is a crucial stepping stone to more advanced mathematical concepts and problem-solving. Understanding this fundamental operation not only strengthens mathematical skills but also equips you with valuable tools for navigating various aspects of everyday life and specialized fields. From cooking and construction to finance and data analysis, the ability to confidently add fractions is a skill that pays dividends across a broad spectrum of human endeavors.
Latest Posts
Latest Posts
-
What Is A Standardised Score
Sep 24, 2025
-
Define Group Polarization In Psychology
Sep 24, 2025
-
Not Only But Also Synonym
Sep 24, 2025
-
What Is Tetrad In Meiosis
Sep 24, 2025
-
3 Properties Of Ionic Compounds
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about One Half Plus One Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.