_ Of 25 Is 15
scising
Sep 21, 2025 · 5 min read
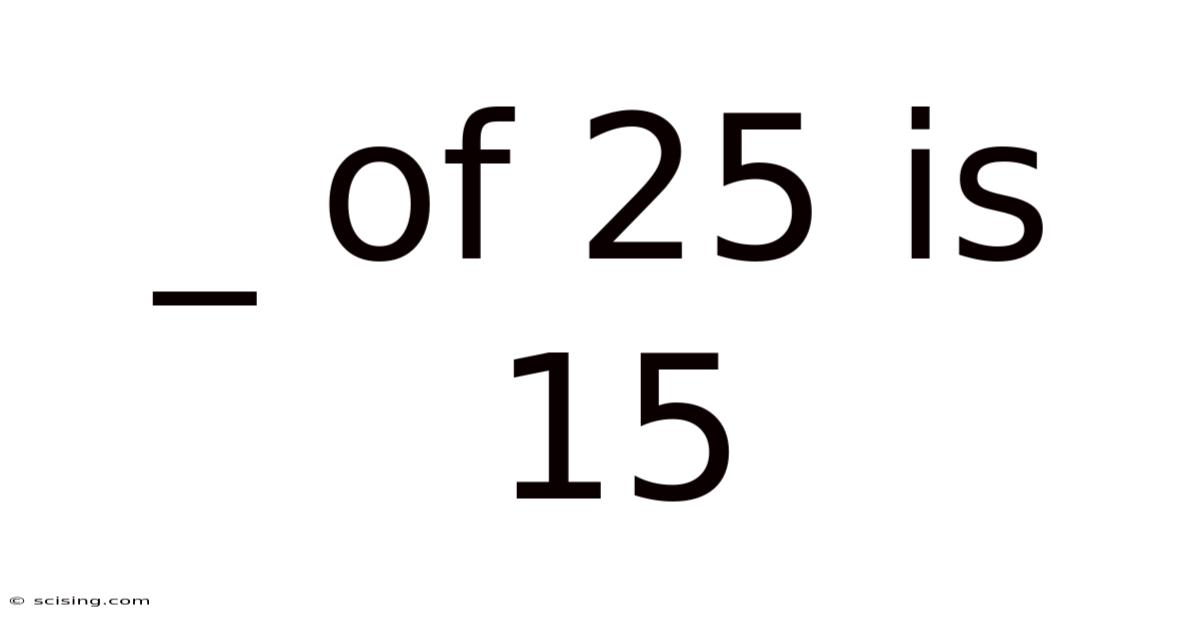
Table of Contents
What Percentage of 25 is 15? A Deep Dive into Percentages and Their Applications
Finding what percentage of 25 is 15 is a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding statistical data and financial reports. This article will not only show you how to solve this specific problem but will also provide a comprehensive understanding of percentages, their calculation, and their practical uses. We'll explore different methods of solving percentage problems, delve into the underlying mathematical principles, and address common misconceptions. By the end, you'll be equipped to confidently tackle any percentage-related problem.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (per centum in Latin). So, 15% means 15 out of 100, or 15/100. This can be expressed as a decimal (0.15) or a fraction (15/100, which simplifies to 3/20). Understanding this fundamental definition is key to solving percentage problems.
Method 1: Using Proportions to Find the Percentage
This method is based on setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion to solve "What percentage of 25 is 15?" as follows:
-
Let x represent the unknown percentage.
-
We can write the proportion as: x/100 = 15/25
-
Cross-multiply: 25x = 1500
-
Solve for x: x = 1500 / 25 = 60
-
Therefore, 15 is 60% of 25.
Method 2: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our problem:
-
Part = 15 (the amount we're interested in)
-
Whole = 25 (the total amount)
Substituting these values into the formula:
(15 / 25) * 100 = 60%
This confirms that 15 is 60% of 25.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to get the percentage.
-
Convert the fraction 15/25 to a decimal: 15 ÷ 25 = 0.6
-
Multiply the decimal by 100 to express it as a percentage: 0.6 * 100 = 60%
This method is particularly useful when dealing with more complex fractions or when using a calculator.
Real-World Applications: Where Percentages Matter
Understanding percentages is crucial in numerous aspects of daily life and various professional fields. Here are some examples:
-
Shopping and Discounts: Calculating discounts on sale items. For example, if a $50 item is 20% off, you would calculate 20% of $50 to find the discount amount.
-
Taxes: Calculating sales tax or income tax. Understanding tax rates and how they are applied to your purchases or income.
-
Finance: Analyzing interest rates on loans or investments. Understanding compound interest and how it affects your savings or debt.
-
Statistics and Data Analysis: Interpreting statistical data presented as percentages. Understanding concepts like percentages change, percentage points, and their significance in representing data trends.
-
Science: Expressing concentrations of solutions or experimental results as percentages. This is particularly important in fields like chemistry and biology.
-
Business: Calculating profit margins, analyzing market share, and understanding key performance indicators (KPIs) expressed as percentages.
-
Everyday Life: Estimating tips at restaurants, comparing prices of products, and calculating proportions of ingredients in recipes.
Common Misconceptions about Percentages
Several common misconceptions surround the use and interpretation of percentages:
-
Confusing percentage change with percentage points: A percentage change refers to the relative change between two values, while percentage points refers to the absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage.
-
Incorrectly calculating percentages of percentages: You can't simply add or subtract percentages directly unless they are referring to the same base value. For example, a 10% discount followed by a further 20% discount is not a 30% discount overall.
-
Misinterpreting percentages in context: The meaning of a percentage can heavily depend on the context. A small percentage might be significant in certain situations (e.g., a small percentage increase in a very large population), while a large percentage might be insignificant in others.
Advanced Percentage Problems and Calculations
While the problem "What percentage of 25 is 15?" is relatively straightforward, percentage problems can become more complex. Here are some examples:
-
Finding the whole when given the percentage and part: If 30% of a number is 60, what is the number?
-
Finding the part when given the percentage and the whole: What is 15% of 80?
-
Calculating percentage increase or decrease: A product's price increased from $100 to $120. What is the percentage increase?
These problems can be solved using variations of the percentage formula or by setting up proportions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators are very helpful, especially for more complex calculations. Most calculators have a percentage function (%) that simplifies the process.
Q: What if the "whole" number is not a whole number?
A: The same methods apply. You'll just be working with decimal numbers instead of whole numbers.
Q: Are there any online tools to help with percentage calculations?
A: Yes, many websites offer online percentage calculators that can assist with various percentage-related problems. Simply search for "percentage calculator" on your preferred search engine.
Q: Why is understanding percentages important?
A: Percentages are used in numerous aspects of life to express proportions, ratios, and changes in quantities. Understanding them is fundamental to making informed decisions in various contexts, from personal finance to professional settings.
Q: How can I improve my skills in solving percentage problems?
A: Practice is key! The more you solve percentage problems, the more comfortable and proficient you will become. Start with simple problems and gradually move towards more complex ones. Also, review the different methods and choose the one that works best for you.
Conclusion
Determining that 15 is 60% of 25 is a simple yet illustrative example of a fundamental mathematical concept. Understanding percentages is not just about solving mathematical problems; it's about developing critical thinking skills and improving your ability to interpret and apply numerical data in everyday life and various professional contexts. By mastering the different methods discussed in this article and practicing regularly, you will build a strong foundation in percentage calculations and confidently tackle a wide range of problems involving this crucial concept. Remember that the key lies not only in memorizing the formulas but in understanding the underlying principles and applying them flexibly to diverse scenarios.
Latest Posts
Latest Posts
-
The Doctor From Canterbury Tales
Sep 21, 2025
-
How To Calculate Resultant Vector
Sep 21, 2025
-
Additive Property Of Angle Measure
Sep 21, 2025
-
37 6 Degrees Celsius To Fahrenheit
Sep 21, 2025
-
Is Grass An Abiotic Factor
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about _ Of 25 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.